Giriş
Rastgele Orman (RF) algoritması , 2001 yılında Breiman tarafından karar ağaçlarının bir kombinasyonu olarak önerilmiştir. RF en iyi “her ağaç, bağımsız olarak örneklenen ve ormandaki tüm ağaçlar için aynı dağılıma sahip rastgele bir vektörün değerlerine bağlı olacak şekilde ağaç belirleyicilerinin kombinasyonu” olarak tanımlanan bir topluluk makine öğrenme algoritmasıdır. Topluluk algoritması gerek regresyon gerekse sınıflandırma problemlerinde varyansı ve hatayı azaltarak daha iyi hedef değişken veya bağımlı değişkeni tahmin etmemize olanak tanır. Bunu da yeniden örnekleme yöntemi (bootstrap aggregation or bagging)’yle yapar. Bu yöntemde sırasıyla tesadüfi tekrarlı örneklem yöntemi (simple random sampling with replacement) kullanılarak veri seti alt örneklem kümelerine, diğer bir ifade ile alt örneklem ağaç kümelerine ayrılır. Bunların tamamı kurulan modelde hatayı azaltmaya yöneliktir. Anlatılanı Şekil 1 üzerinde gösterelim. Şekilde modellerin paralel düzende inşa edildiğine dikkat etmek gerekir. Modellerin oluşturulmasında çaprazlama bulunmamaktadır.
Şekil 1: Rastgele Orman Algoritmasında Yeniden Örnekleme (Bootstrapping)

RF, karar ağaçlarına dayanır. Makine öğreniminde karar ağaçları, tahmin modelleri oluşturan denetimli öğrenme tekniğidir. Bunlara karar ağaçları (decision trees) adı verilmektedir. Bu yöntemin özellikle mühendislik bilimlerinde başta sağlık sektörü olmak üzere pek çok sektörde yaygın bir şekilde kullanıldığı görülmektedir.
Rastgele orman algoritmaları hem sınıflandırma (classification) hem de regresyon (regression) problemlerinin çözümünde kullanılan makine öğrenmenin denetimli öğrenme (supervised) kısmında yer alan tahmin oranı yüksek algoritmalardır. Burada aslında sınıflandırma ve regresyondan kasıt tahmin edilecek bağımlı veya hedef değişkenin veri tipi ifade edilmektedir. Sınıflandırma ve regresyon için kullanılan veri tipleri Şekil 2’de sunulmuştur. Cevap değişkeni ya da bağımlı değişken kategorik ise rastgele orman algoritmasında sınıflandırma, bağımlı değişken nicel ise rastgele orman algoritmasında regresyon problemini çözmüş oluyoruz. RF analizlerde uç değerler (outliers)’e duyarlı değildir.
Şekil 2: Rastgele Orman (RF) Algoritmasında Proplem Sınıfına Göre Veri Tüleri

RF’te kurulan modelin veya modellerin performansını değerlendirmede kullanılan hata metrikleri ise genel itibariyle Şekil 3’te verilmiştir. Şekil 3’te yer verilen hata metrikleri gerek makine öğrenme gerekse derin öğrenme modellerinin performansının testinde sıklıkla kullanılmaktadır.
Şekil 3: Rastgele Orman Algoritması Hata Metrikleri

Şekil 3’te sınıflandırma problemlerinin çözümünde kullanılan hata metriklerini şimdi de ele alalım. Karışıklık matrisi (confusion matrix) olarak olarak adlandırılan bu matris sınıflandırma problemlerinin çözümünde hata metriklerini ortaya koyarak kurulan modelin veya modellerin hata oranını değerlendirmektedir. Hata matrisinin makine ve derin öğrenme metotlarının değerlendirilmesinde sıklıkla kullanıldığı görülmektedir. Aşağıda yer alan tabloda hata metriklerinin hesaplanmasına esas teşkil eden tablo verilmiştir. Bu tabloyla sınıflandırma hataları hesaplanabilmektedir. Tabloda yer verilen Tip 1 hata (Type 1 error) istatistikte alfa hatasını göstermektedir. Tip 1 hata H0 hipotezi (null hpypothesis) doğru olduğu halde reddedilmesidir. Tabloda Tip 2 hata (Type II error) olarak adlandırılan hata ise istatistikte Beta hatası olarak da bilinmektedir. Tip 2 hata ise H0 hipotezi (null hpypothesis) yanlış olduğu halde kabul edilmesidir.

Şekil 3’te de yer verildiği üzere literatürde sınıflandırma modellerinin performansını değerlendirmede aşağıdaki metriklerden yaygın bir şekilde yararlanıldığı görülmektedir. Sınıflandırma problemlerinin çözümüne yönelik Rastgele Orman Algoritması (RF) kullanarak R’da yapmış olduğum çalışmanın linkini ilgilenenler için aşağıda veriyorum.
Sınıflandırma Metrikleri
- Doğruluk (Accuracy): TP+TN / TP+TN+FP+FN eşitliği ile hesaplanır. Modelin genel performansını ortaya koyar. Bu sınıflandırma metriği ile aslında biz informal bir şekilde dile getirirsek doğru tahminlerin toplam tahminler içindeki oranını hesaplamış oluyoruz.
- Kesinlik (Precision): TP / TP+FP eşitliği ile hesaplanır. Doğru tahminlerin ne kadar kesin olduğunu gösterir.
- Geri çağırma (Recall): TP / TP+FN eşitliği ile hesaplanır. Gerçek pozitif örneklerin oranını verir.
- Özgünlük (Specificity): TN / TN+FP eşitliği ile hesaplanır. Gerçek negatif örneklerin oranını gösterir.
- F1 skoru : 2TP / 2TP+FP+FN eşitliği ile hesaplanır. Dengesiz sınıflar için yararlı hibrit bir metrik olup, kesinlik (precision) ve geri çağırma (recall) skorlarının ağırlıklı ortalamasını ifade etmektedir.
- ROC (Receiver operating characteristic): Yukarıda karışıklık matrisinde belirtilen parametrelerden yararlanılarak hesaplanır. ROC eğrisi olarak da adlandırılmaktadır. ROC eğrileri, herhangi bir tahmin modelinin doğru pozitifler (TP) ve negatifler (TN) arasında nasıl ayrım yapabileceğini görmenin güzel bir yoludur. Sınıflandırma modellerin perfomansını eşik değerler üzerinden hesaplar. ROC iki parametre üzerinden hesaplanır. Doğru Pozitiflerin Oranı (TPR) ve Yanlış Pozitiflerin Oranı (FPR) bu iki parametreyi ifade eder. Burada aslında biz TPR ile Geri Çağırma (Recall), FPR ile ise 1-Özgünlük (Specificity)‘ü belirtiyoruz.
- Cohen Kappa: Kategorik cevap seçenekleri arasındaki tutarlılığı ve uyumu gösterir. Cohen, Kappa sonucunun şu şekilde yorumlanmasını önermiştir: ≤ 0 değeri uyumun olmadığını, 0,01–0,20 çok az uyumu, 0,21-0,40 az uyumu, 0,41-0,60 orta, 0,61-0,80 iyi uyumu ve 0,81–1,00 çok iyi uyumu göstermektedir. 1 değeri ise mükemmel uyum anlamına gelmektedir.
Şekil 3’te yer verilen regresyon modellerinin performansını değerlendirmede literatürde aşağıdaki metriklerden yaygın bir şekilde yararlanılmaktadır. Regresyon metrikleri eştiliklerinin verilmesi yerine sade bir anlatımla neyi ifade ettiği anlatılacaktır. Böylece formüllere boğulmamış olacaksınız.
Regresyon Metrikleri
- SSE (Sum of Square Error): Tahmin edilen değerler ile gözlem değerleri arasındaki farkların kareleri toplamını ifade eder.
- MSE (Mean Square Error): Ortalama kare hatası olarak adlandırılan bu hata tahmin edilen değerler ile gözlem değerleri arasındaki farkların karelerinin ortalamasını ifade eder.
- RMSE (Root Mean Square Error): Kök ortalama kare hatası olarak adlandırılan bu hata ortalama kare hatasının karekökünü ifade etmektedir.
- MAE (Mean Absolute Error): Ortalama mutlak hata olarak adlandırılan bu hata türü ise tahmin edilen değerler ile gözlem değerleri arasındaki farkların mutlak değerlerinin ortalamasını ifade etmektedir.
- MAPE (Mean Absolute Percentage Error): Ortalama mutlak yüzdesel hata olarak adlandırılan bu hata türünde ilk olarak tahmin edilen değerler ile gözlem değerleri arasındaki farkların mutlak değerleri hesaplanır. Daha sonra hesaplanan farkları mutlak değerleri mutlak değerleri alınan gözlem değerlerine bölünür. En son durumda ise elde edilen bu değerlerin ortalaması alınır.
- Bias: Tahmin edilen değerler ile gözlem değerleri arasındaki farkların ortalamasıdır. Bu yönüyle ortalama mutlak hata (MAE)’ya benzemektedir.
Regresyon metriklerini anlattıktan sonra daha kalıcı olması ve öğrenilmesi adına hazırladığım excel üzerinde bahsedilen bu metriklerin nasıl hesaplandığı gösterilmiştir. Excel dosyasını aşağıdaki linkten indirebilirsiniz.
Metodoloji ve Uygulama Sonuçları
Bu kısımda kullanılan veri setine ve adım adım Rastgele Orman algoritmasının regresyon problemlerinin çözümünde nasıl uygulandığına yer verilmiştir. Analizde R programlama dili kullanılmıştır. Uygulamaya esas veri seti Amerikan Ulusal Ekonomik Araştırmalar Bürosu (the National Bureau of Economic Research) kısa adıyla NBER’in resmi web sitesinden alınmıştır. Web sitesinin linki: https://data.nber.org/ dir. Veri setinin alındığı linkin tam adı ise http://data.nber.org/nberces/nberces5811/naics5811.xls dir.
Veri seti 1958’den 2011’e kadar ABD imalat sektöründeki katma değer ve toplam faktör verimliliği (TFV) göstergelerinden oluşan zengin ve hacmi geniş bir veri setidir. Orjinal (ingilizce) xlsx uzantılı veri setini aşağıdaki linkten indirebilirsiniz. Veri setindeki toplam gözlem sayısı 25542, değişken sayısı ise 25’tir.
R’da analize uygun hale getirdiğim aynı veri setinin Türkçe versiyonunu ise aşağıdaki linkten indirebilirsiniz. Veri setinin Türkçeye çevrilmesinin nedeni anlaşılırlığın artırılmak istenmesidir.
Veri seti “sira” hariç 8 değişkenden oluşmakta olup, anlaşılırlığı artırmak adına Türkçeye çevrilmiştir. Değişkenlerin tamamının veri türü nicel ve sürekli olup orjinal (ingilizce) adlarıyla birlikte aşağıda verilmiştir:
- tistihdam: Toplam istihdamı göstermekte olup, orjinal veri setindeki adı “emp” dir. İstihdam değerleri 1000’e bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- maas: Sektör çalışanlarının maaşlarını göstermekte olup, orjinal veri setindeki adı “pay” dir. Maaş değerleri 1 milyon $’a bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- iistihdam: Üretim bandında çalışanların sayısını göstermekte olup, orjinal veri setindeki adı “prode” dur. Çalışan sayısı değerleri 1000’e bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- icsaati: Üretim bandında çalışanların çalışma saatlerini göstermekte olup, orjinal veri setindeki adı “prodeh” dır. Çalışma saatleri 1 milyona bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- sbu: Üretim bandında çalışanların ücretlerini göstermekte olup, orjinal veri setindeki adı “prodew” dır. Çalışma ücretleri 1 milyon $’a bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- netsatis: Ne satışları göstermekte olup, orjinal veri setindeki adı “vship” tir. Net satışlar 1 milyon $’a bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- mmaliyeti: Malzeme maliyetlerini göstermekte olup, orjinal veri setindeki adı “matcost” tur. Maliyetler 1 milyon $’a bölünerek verilmiştir. Bağımsız değişken olarak alınmıştır.
- katmadeger: Katma değeri göstermekte olup, orjinal veri setindeki adı “vadd” tir. Katma değer 1 milyon $’a bölünerek verilmiştir. Bağımlı / hedef değişken (target variable) olarak alınmıştır.
Çalışmanın amacı yukarıda belirtilen bağımsız değişkenler ile bağımlı değişken olan “katmadeger” değişkenini tahmin etmektir.
Metodoloji ve uygulama sonuçları başlığı altında Rastgele Orman algoritmasına üzerine kurulan modeller olabilecek en yalın şekilde karşılaştırmalı olarak ele alınmaya çalışılmıştır. Daha sonra kurulan bu modeller hata metrikleri açısından karşılaştırılmıştır.
Analize başlamadan önce analiz için yüklenecek R kütüphaneleri verelim. Ardından keşifsel veri analizi (EDA) ile veri setini tanıyalım.
Yüklenecek kütüphaneler
kütüphaneler = c("dplyr","tibble","tidyr","ggplot2","formattable","readr","readxl","xlsx", "pastecs","randomForest", "aod", "DescTools", "ggpurr","psych","writexl","ggfortify", "caret","Metrics", "performanceEstimation", "yardstick","MASS")
sapply(kütüphaneler, require, character.only = TRUE)
Veri setinin kaynak web sitesinden okunması
url <- "http://data.nber.org/nberces/nberces5811/naics5811.xls"
dosyaadi <- "naics5811.xls"
curl::curl_download(url, dosyaadi)
veri <- read_excel(dosyaadi)
veri
Veri setinin Türkçeye dönüştürülmesi ve analiz değişkenlerinin belirlenmesi
df<-veri[,3:10] %>% as_tibble() %>% rename(tistihdam=emp, maas=pay, iistihdam=prode, icsaati=prodh, sbu=prodw, netsatis=vship, mmaliyeti=matcost, katmadeger=vadd) %>% rowid_to_column() %>% rename(sira=rowid)
df
Veri setindeki eksik gözlemlerin (Missing Data: NA) tespit edilmesi ve veri setinden çıkarılması
#Eksik gözlemlerin (NAs) sayısının değişkene göre belirlenmesi
nan<-sapply(df, function(x) sum(is.na(x))) %>% as_tibble()
nan<-cbind(Değişken=names(df), n=nan) %>% as_tibble()
formattable(nan)
#Eksik gözlemlerin (NAs) veri setinden çıkarılması
df1<-na.omit(df)
nan1<-sapply(df1, function(x) sum(is.na(x))) %>% as_tibble()
nan1<-cbind(Değişken=names(df), n=nan1) %>% as_tibble()
formattable(nan1)
#ilk 10 kayıt
formattable(head(df1, 10))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setinde değişkenlere göre belirlenen eksik veri (NA) diğer bir ifadeyle eksik gözlem sayısı aşağıdaki tabloda verilmiştir.
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setinde değişkenlere göre belirlenen eksik gözlemler veri setinden çıkarılmış olup aşağıdaki tabloda son durumda veri setindeki eksik gözlem sayıları gösterilmiştir.
Veri setinin xlsx dosyasına yazdırılması
İhtiyaç duymanız halinde fonksiyonu ile birlikte eksik gözlemler (NAs)’den arındırılmış veri seti aşağıdaki kod yardımıyla xlsx uzantılı olarak excel dosyasına yazdırılmıştır.
writexl::write_xlsx(df1, "verisetiturkcekayipsizveri.xlsx")
Yukarıdaki R kod bloğunun çalıştırılması ile edilen veri seti dosyası xlsx uzantılı olarak aşağıda verilmiştir.
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen veri setinin ilk 10 satırı aşağıda verilmiştir.

Veri setindeki değişkenlerin özellikleri
str(df1)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki değişkenlerin veri tipleri, gözlem sayılarıyla birlikte aşağıda verilmiştir.
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 25386 obs. of 9 variables:
$ sira : int 1 2 3 4 5 6 7 8 9 10 ...
$ tistihdam : num 18 17.9 17.7 17.5 17.6 17.1 16.6 16 16.1 16.7 ...
$ maas : num 81.3 82.5 84.8 87.4 90.2 89.8 90.8 90.8 96.1 105 ...
$ iistihdam : num 12 11.8 11.7 11.5 11.5 11 10.6 10.2 10.2 11 ...
$ icsaati : num 25.7 25.5 25.4 25.4 25.2 23.9 23.5 22.7 22.6 23.9 ...
$ sbu : num 49.8 49.4 50 51.4 52.1 52.1 52.2 51.8 53.9 61.3 ...
$ netsatis : num 1042 1051 1050 1120 1176 ...
$ mmaliyeti : num 752 759 753 804 853 ...
$ katmadeger: num 267 269 270 288 294 ...
- attr(*, "na.action")= 'omit' Named int 1729 1730 1731 1732 1733 1734 1735 1736 1737 1738 ...
..- attr(*, "names")= chr "1729" "1730" "1731" "1732" ...
Tanımlayıcı istatistikler
ti<-describe(df1[,-1])
formattable(tibble(Değişken=names(df1[,-1]), Aralık=ti$range, Ort=ti$mean, Medyan=ti$median, Ssapma=ti$sd, Carpıklık=ti$skew, Basıklık=ti$kurtosis) %>% mutate_if(is.numeric, round, 1))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tanımlayıcı istatistikler aşağıdaki tabloda verilmiştir.

Değişkenler arasındaki korelasyon
Nicel ve sürekli değişkenlerin korelasyon katsayılarını hesaplamak için Pearson korelasyon katsayısı kullanılmış olup, yazılan R kod bloğu aşağıdadır.
com<-round(cor(df1[,-1]), 1)
com<-cbind(Değisken=names(df[,-1]), com) %>% as_tibble()
formattable(com)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen korelasyon katsayıları aşağıdaki tabloda verilmiştir.

Veri setinin eğitilecek veri ve test setine ayrılması
set.seed(1919)
#Eğitilecek veri seti (training set)
train1 <- df1 %>% sample_frac(.70)
train1
#Test edilecek veri seti
test1 <- anti_join(df1, train1, by = 'sira')#Anti join fonksiyonu eşleşmeyen kayıtları yani geri kalan kayıtları getirir ve onları test setine atar.
test1
Model 1
1 nolu modelin oluşturulması
model1<-randomForest(katmadeger ~ ., train1[,-1])
print(model1)
summary(model1)
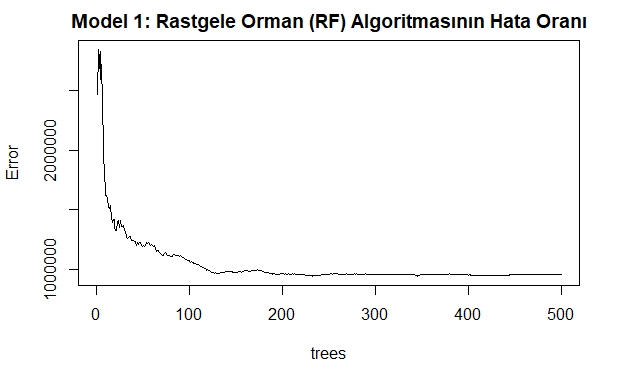
plot(model1, main="Model 1: Rastgele Orman (RF) Algoritmasının Hata Oranı")
Yukarıdaki kod bloğunun çalıştırılmasından sonra kurulan modele ilişkin açıklanan varyans (% 96,05) aşağıda verilmiştir.
Call:
randomForest(formula = katmadeger ~ ., data = train1[, -1])
Type of random forest: regression
Number of trees: 500
No. of variables tried at each split: 2
Mean of squared residuals: 956776.9
% Var explained: 96.05
Yukarıdaki kod bloğunun çalıştırılmasından sonra çizilen modelin grafiği aşağıda verilmiştir. Bu grafik rastgele orman modelindeki regresyon hata oranlarını göstermektedir. Ağaç sayısı (ntree) arttıkça hata oranı sıfıra yaklaşır ve belirli noktadan sonra durağanlaşır. Burada ağaç sayısının az olması elde edilecek sonuçların varyansını artırarak hatayı yükseltir.
1 nolu modeldeki değişkenlerin önem düzeyleri
k<-importance(model1)
k<-tibble(Değişken=as.vector(row.names(k)), Dugum_Safligi=as.vector(importance(model1)))%>%arrange(desc(Dugum_Safligi))
formattable(k,
list(formatter(
"span", style = ~ style(color = "grey",font.weight = "bold")),
`Dugum_Safligi` = color_bar("#00FF7F")
))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeyleri düğüm saflıkları (Inc Node Purity)’na göre büyükten küçüğe doğru aşağıdaki tabloda verilmiştir.

Tahmin edilen değerler ile gözlem değerlerinin karşılaştırılması
pred1<-predict(model1, test1)
karsilastirma<-tibble(Gercek=test1$katmadeger, Tahmin=pred1)
#ilk ve son 10 tahmin değerini gerçek değerle karşılaştırma
ilk10<-head(karsilastirma, 10) %>% rename(Gercekİlk_10=Gercek, Tahminİlk_10=Tahmin) %>% mutate_if(is.numeric, round, 1)
son10<-tail(karsilastirma, 10) %>% rename(GercekSon_10=Gercek, TahminSon_10=Tahmin) %>% mutate_if(is.numeric, round, 1)
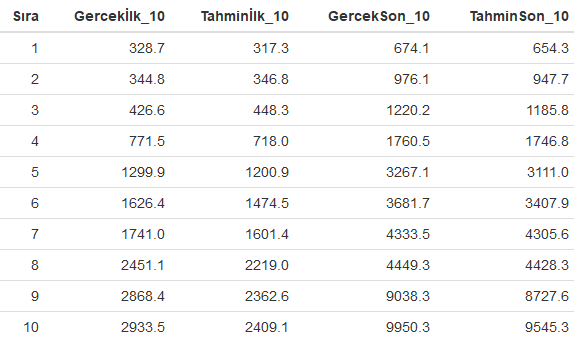
formattable(cbind(Sıra=seq(1,10),ilk10, son10))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modelden elde edilen ilk ve son 10 gözlem değerleri ile tahmin değerleri aşağıdaki tabloda karşılaştırmalı olarak verilmiştir.
Regresyon metrikleri
Kurulan 1 nolu modele ait hata metriklerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.
karsilastirma<-tibble(Gercek=test1$katmadeger, Tahmin=pred1)
metrik<-tibble(SSE=sse(karsilastirma$Gercek, karsilastirma$Tahmin), MSE=mse(karsilastirma$Gercek, karsilastirma$Tahmin),RMSE=rmse(karsilastirma$Gercek, karsilastirma$Tahmin), MAE= mae(karsilastirma$Gercek, karsilastirma$Tahmin),MAPE= mape(karsilastirma$Gercek, karsilastirma$Tahmin), Bias= bias(karsilastirma$Gercek, karsilastirma$Tahmin))%>% mutate_if(is.numeric, round, 1)
formattable(metrik)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait hata parametre değerleri aşağıda verilmiştir.

Çapraz performans testi (Cross validation test)
Çapraz performans testi veri setindeki gözlem sayısına ve bilgisayar işlemci kapasitelerine bağlı olarak uzun sürebilmektedir. Sabırlı olmakta fayda var 🙂
set.seed(1919)
cv<- performanceEstimation(
PredTask(katmadeger ~ ., df1[,-1]),
workflowVariants(learner=("randomForest")),
EstimationTask(metrics = c("mse", "mae", "rmse"),
method = CV(nReps = 1, nFolds = 10)))
summary(cv)
plot(cv)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.
== Summary of a Cross Validation Performance Estimation Experiment ==
Task for estimating mse,mae,rmse using
1 x 10 - Fold Cross Validation
Run with seed = 1234
* Predictive Tasks :: df1[, -1].katmadeger
* Workflows :: randomForest
-> Task: df1[, -1].katmadeger
*Workflow: randomForest
mse mae rmse
avg 757383.7 195.22316 842.1489
std 399589.1 17.73925 231.3462
med 600792.8 190.91481 774.9974
iqr 722966.5 27.63886 415.4534
min 277804.7 168.18802 527.0718
max 1310045.6 222.07900 1144.5722
invalid 0.0 0.00000 0.0000
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıdaki grafikte verilmiştir.

Model 2
2 nolu modelin oluşturulması
which.min(model1$mse)#1. modelde büyütülecek ağaçlarının sayısını minimum yapan hata
set.seed(1920)
model2<-randomForest(katmadeger ~ ., train1[,-1], ntree=54, mtry=8/3)#modelde mtyr her bölümde rastgele aday olarak örneklenen değişken sayısını (p=değişken sayısı/3) göstermektedir.
print(model2)
summary(model2)
plot(model2, main="Model 2: Rastgele Orman (RF) Algoritmasının Hata Oranı")
Yukarıdaki kod bloğunun çalıştırılmasından sonra kurulan modele ilişkin açıklanan varyans (% 97,26) aşağıda verilmiştir.
Call:
randomForest(formula = katmadeger ~ ., data = train1[, -1], ntree = 54, mtry = 8/3)
Type of random forest: regression
Number of trees: 54
No. of variables tried at each split: 3
Mean of squared residuals: 719121.7
% Var explained: 97.26
Yukarıdaki kod bloğunun çalıştırılmasından sonra çizilen modelin grafiği aşağıda verilmiştir. Bu grafik rastgele orman modelindeki regresyon hata oranlarını göstermektedir. Ağaç sayısı (ntree) arttıkça hata oranı sıfıra yaklaşır ve belirli noktadan sonra durağanlaşır. Burada ağaç sayısının çok az veya fazla olması elde edilecek sonuçların varyansını artırarak hatayı yükseltebilir.

2 nolu modeldeki değişkenlerin önem düzeyleri
k<-importance(model2)
k<-tibble(Değişken=as.vector(row.names(k)), Dugum_Safligi=as.vector(importance(model2)))%>%arrange(desc(Dugum_Safligi))
k
formattable(k,
list(formatter(
"span", style = ~ style(color = "grey",font.weight = "bold")),
`Dugum_Safligi` = color_bar("#B0C4DE")
))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeyleri düğüm saflıkları (Inc Node Purity)’na göre büyükten küçüğe doğru aşağıdaki tabloda verilmiştir.

Regresyon metrikleri
Kurulan 2 nolu modele ait hata metriklerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.
pred2<-predict(model2, test1)
karsilastirma2<-tibble(Gercek=test1$katmadeger, Tahmin=pred2)
metrik<-tibble(SSE=sse(karsilastirma2$Gercek, karsilastirma2$Tahmin), MSE=mse(karsilastirma2$Gercek, karsilastirma2$Tahmin),RMSE=rmse(karsilastirma2$Gercek, karsilastirma2$Tahmin), MAE= mae(karsilastirma2$Gercek, karsilastirma2$Tahmin),MAPE= mape(karsilastirma2$Gercek, karsilastirma2$Tahmin), Bias= bias(karsilastirma2$Gercek, karsilastirma2$Tahmin))%>% mutate_if(is.numeric, round, 1)
formattable(metrik)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait hata parametre değerleri aşağıda verilmiştir.

set.seed(1920)
cv<- performanceEstimation(
PredTask(katmadeger ~ ., df1[,-1]),
workflowVariants(learner="randomForest", learner.pars=list(ntree=54, mtry=8/3)),
EstimationTask(metrics = c("mse", "mae", "rmse"),
method = CV(nReps = 1, nFolds = 10)))
summary(cv)
#rankWorkflows(cv, top = 3)
plot(cv)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.
== Summary of a Cross Validation Performance Estimation Experiment ==
Task for estimating mse,mae,rmse using
1 x 10 - Fold Cross Validation
Run with seed = 1234
* Predictive Tasks :: df1[, -1].katmadeger
* Workflows :: randomForest
-> Task: df1[, -1].katmadeger
*Workflow: randomForest
mse mae rmse
avg 620028.2 154.33328 767.2455
std 311613.2 14.63084 186.6741
med 545472.8 154.55071 736.9520
iqr 295773.3 20.45502 201.6927
min 309424.4 123.09429 556.2593
max 1231557.9 167.92314 1109.7558
invalid 0.0 0.00000 0.0000
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değerleri aşağıdaki grafikte verilmiştir.

Sonuç
Bu çalışmada regresyon (regression) probleminin çözümüne yönelik Rastgele Orman (RF) algoritması kullanılarak ayrıntılı deneysel bir çalışma yapılmıştır. Ortaya konulan bulgular, kurulan regresyon modelleri içerisinde 1. modeldeki bağımsız değişkenler bağımlı değişkendeki varyansın % 96’sını, 2. model ise varyansın % 97’sini açıklamaktadır. Modellere ilişkin çapraz performans testi sonuçları aşağıdaki tabloda verilmiş olup, 2. modelde üretilen ortalamalar hatalar 1. modele göre daha az olduğu için 2. model bağımlı değişken olan “katmadeger” i daha iyi tahmin ettiği söylenebilir.
| Model | MSE | MAE | RMSE |
| Model 1 | 757383.7 | 195.2 | 842.2 |
| Model 2 | 620028.2 | 154.3 | 767,3 |
Yapılan bu çalışmanın özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına önemli bir katkı sunacağı düşünülmektedir.
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
- https://data.nber.org/info.html
- https://archive.ics.uci.edu/ml/machine-learning-databases/car/
- https://www.r-project.org/
- https://www.census.gov/manufacturing/m3/definitions/index.html
- http://data.nber.org/data/nberces.html
- http://data.nber.org/nberces/nberces5811/naics5811.xls
- https://www.shirin-glander.de/2018/10/ml_basics_rf/
- Breiman, L. Random Forests. Machine Learning 45, 5–32 (2001). https://doi.org/10.1023/A:1010933404324
- https://github.com/ltorgo/performanceEstimation
- An evaluation of Guided Regularized Random Forest for classification and regression tasks in remote sensing. https://doi.org/10.1016/j.jag.2020.102051
- https://rstudio-pubs-static.s3.amazonaws.com/293333_2a434ee651164113831a9d2e799f2f68.html
- https://stanford.edu/~shervine/l/tr/teaching/cs-229/cheatsheet-machine-learning-tips-and-tricks
- https://tevfikbulut.com/2020/05/10/ordinal-lojistik-regres-uzerine-bir-vaka-calismasi-a-case-study-on-ordinal-logistic-regression/
- Predicting the protein structure using random forest approach. Charu Kathuria, Deepti Mehrotra, Navnit Kumar Misra. International Conference on Computational Intelligence and Data Science (ICCIDS 2018).
- Random Forest ensembles for detection and prediction of Alzheimer’s disease with a good between-cohort robustness. NeuroImage: Clinical Volume 6, 2014, Pages 115-125. https://doi.org/10.1016/j.nicl.2014.08.023
- Breiman, L (2002), “Manual On Setting Up, Using, And Understanding Random Forests V3.1”,
- https://www.stat.berkeley.edu/~breiman/Using_random_forests_V3.1.pdf
- https://www.stat.berkeley.edu/~breiman/RandomForests/
- https://stats.idre.ucla.edu/r/library/r-library-introduction-to-bootstrapping/
- McHugh M. L. (2012). Interrater reliability: the kappa statistic. Biochemia medica, 22(3), 276–282.
- Lange R.T. (2011) Inter-rater Reliability. In: Kreutzer J.S., DeLuca J., Caplan B. (eds) Encyclopedia of Clinical Neuropsychology. Springer, New York, NY
- https://www.theanalysisfactor.com/what-is-an-roc-curve/
- https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc
- https://tevfikbulut.com/2020/05/14/rastgele-orman-algoritmasina-uzerine-bir-vaka-calismasi-a-case-study-on-random-forest-rf-algorithm/