R Programlama Diliyle Sınıflandırma Problemlerinin Çözümünde Küme Algoritmaları Üzerine Bir Vaka Çalışması: A Case Study on Cluster Algorithms in Solving Classification Problems with R Programming Language

Giriş

Küme geçmeden önce temel kavramları açıklamak konunun anlaşılması açısından önem taşıdığından ilk olarak kısaca bu kavramlara yer verilmiştir.

Küme, benzer özellikleri içinde barındıran topluluk olarak tanımlanabilir. Bu topluluk insan, hayvan, bitki topluluğu olabileceği gibi nesnelerin oluşturduğu topluluk da olabilir. Benzer özellikler taşıyan bu topluluklar diğer kümelerden farklılaşır.

Kümeleme (clustering) analizini ise benzer özelliklere sahip toplulukları gruplara ayırma olarak açıklayabiliriz. Bu analizle bir nevi gruplama yapılmaktadır. Bu analiz türü aynı zamanda yapay zeka öğrenme türlerinden biri olan denetimsiz öğrenme (unsupervised learning)’nin denetimsiz sınıflama (unsupervised classification) başlığı altında değerlendirilir. Çünkü denetimli öğrenme (supervised learning)’de veri önceden tanımlanmış değildir veya önceden sınıflama (denetimli sınıflama) durumu bu analiz türünde söz konusu değildir. Küme analizi bir çok alanda kullanılabilmekle birlikte öne çıkan alanlar şöyle özetlenebilir;

• Hastalık Teşhisi
• Tedavi Yöntemleri
• Sigorta
• Pazarlama
• Arazi kullanımı
• Şehir planlama

Küme Analiz Metodları

• Herüstik yaklaşımlar
  1. K-Ortalama (k-means) Küme Analiz Metodu: Her bir küme, kümenin merkez noktasıyla temsil edilir.
  2. K-Medoidler (k-medoids) veya PAM Küme Analiz Metodu: Her bir küme, kümedeki nesnelerden biri tarafından temsil edilir.

Küme analizinin kalitesi, sınıf içi benzerlikleri yüksek (varyans düşük) ve kümeler arası benzerliklerin düşük (varyans yüksek) kümelerin elde edilmesine bağlıdır.

Küme algoritmaları hem sınıflandırma (classification) hem de regresyon (regression) problemlerinin çözümünde kullanılan makine öğrenmenin denetimsiz öğrenme (unsupervised) kısmında yer alan algoritmalardır. Burada aslında sınıflandırma ve regresyondan kasıt tahmin edilecek bağımlı veya hedef değişkenin veri tipi ifade edilmektedir. Sınıflandırma ve regresyon için kullanılan veri tipleri Şekil 2’de sunulmuştur. Cevap değişkeni ya da bağımlı değişken kategorik ise küme algoritmalarında sınıflandırma, bağımlı değişken nicel ise küme algoritmalarında regresyon problemini çözmüş oluyorur.

Şekil 2: Küme Analizlerinde Problem Sınıfına Göre Veri Türleri

Küme analizlerinde kurulan modelin veya modellerin performansını değerlendirmede kullanılan hata metrikleri ise genel itibariyle Şekil 3’te verilmiştir. Şekil 3’te yer verilen hata metrikleri gerek makine öğrenme gerekse derin öğrenme modellerinin performansının testinde sıklıkla kullanılmaktadır.

Şekil 3: Hata Metrikleri

Şekil 3’te sınıflandırma problemlerinin çözümünde kullanılan hata metriklerini şimdi de ele alalım. Karışıklık matrisi (confusion matrix) olarak olarak adlandırılan bu matris sınıflandırma problemlerinin çözümünde hata metriklerini ortaya koyarak kurulan modelin veya modellerin hata oranını değerlendirmektedir. Hata matrisinin makine ve derin öğrenme metotlarının değerlendirilmesinde sıklıkla kullanıldığı görülmektedir. Aşağıda yer alan tabloda sınıflandırma problemlerinde hata metriklerinin hesaplanmasına esas teşkil eden tablo verilmiştir. Bu tabloyla sınıflandırma hataları hesaplanabilmektedir. Tabloda yer verilen Tip 1 hata (Type 1 error) istatistikte alfa hatasını göstermektedir. Tip 1 hata H0 hipotezi (null hpypothesis) doğru olduğu halde reddedilmesidir. Tabloda Tip 2 hata (Type II error) olarak adlandırılan hata ise istatistikte Beta hatası olarak da bilinmektedir. Tip 2 hata ise H0 hipotezi (null hpypothesis) yanlış olduğu halde kabul edilmesidir.

Şekil 3’te de yer verildiği üzere literatürde sınıflandırma modellerinin performansını değerlendirmede aşağıdaki metriklerden yaygın bir şekilde yararlanıldığı görülmektedir.

• Doğruluk (Accuracy): TP+TN / TP+TN+FP+FN eşitliği ile hesaplanır. Modelin genel performansını ortaya koyar. Bu sınıflandırma metriği ile aslında biz informal bir şekilde dile getirirsek doğru tahminlerin toplam tahminler içindeki oranını hesaplamış oluyoruz.
• Kesinlik (Precision): TP / TP+FP eşitliği ile hesaplanır. Doğru tahminlerin ne kadar kesin olduğunu gösterir.
• Geri çağırma (Recall): TP / TP+FN eşitliği ile hesaplanır. Gerçek pozitif örneklerin oranını verir.
• Özgünlük (Specificity): TN / TN+FP eşitliği ile hesaplanır. Gerçek negatif örneklerin oranını gösterir.
• F1 skoru : 2TP / 2TP+FP+FN eşitliği ile hesaplanır. Dengesiz sınıflar için yararlı hibrit bir metrik olup, kesinlik (precision) ve geri çağırma (recall) skorlarının ağırlıklı ortalamasını ifade etmektedir.
• ROC (Receiver operating characteristic): Yukarıda karışıklık matrisinde belirtilen parametrelerden yararlanılarak hesaplanır. ROC eğrisi olarak da adlandırılmaktadır. ROC eğrileri, herhangi bir tahmin modelinin doğru pozitifler (TP) ve negatifler (TN) arasında nasıl ayrım yapabileceğini görmenin güzel bir yoludur. Sınıflandırma modellerinin performansını eşik değerler üzerinden hesaplar. ROC iki parametre üzerinden hesaplanır. Doğru Pozitiflerin Oranı (TPR) ve Yanlış Pozitiflerin Oranı (FPR) bu iki parametreyi ifade eder. Burada aslında biz TPR ile Geri Çağırma (Recall), FPR ile ise 1-Özgünlük (Specificity)‘ü belirtiyoruz.
• Cohen Kappa: Kategorik cevap seçenekleri arasındaki tutarlılığı ve uyumu gösterir. Cohen, Kappa sonucunun şu şekilde yorumlanmasını önermiştir: ≤ 0 değeri uyumun olmadığını, 0,01–0,20 çok az uyumu, 0,21-0,40 az uyumu, 0,41-0,60 orta, 0,61-0,80 iyi uyumu ve 0,81–1,00 çok iyi uyumu göstermektedir. 1 değeri ise mükemmel uyum anlamına gelmektedir.

Metodoloji ve Uygulama Sonuçları

Bu kısımda kullanılan veri setine ve adım adım küme algoritmalarının uygulamasına yer verilmiştir. Analizde R programlama dili kullanılmıştır. Uygulamaya esas veri seti “iris” bitkisi veri seti olup 150 gözlem ve 6 değişkenden oluşmaktadır. Bu veri seti R’da bulunmaktadır. Veri setindeki değişkenler sırasıyla şöyledir:

1. sepal length (cm) : Veri tipi nicel ve süreklidir.
2. sepal width (cm) : Veri tipi nicel ve süreklidir.
3. petal length (cm) : Veri tipi nicel ve süreklidir.
4. petal width (cm) : Veri tipi nicel ve süreklidir.
5. species (türler) : Veri tipi nitel ve nominaldir.
   — Iris Setosa
   — Iris Versicolour
   — Iris Virginica

Metodoloji ve uygulama sonuçları başlığı altında olabilecek en yalın şekilde ele alınmaya çalışılmıştır. Çalışmada amaç species hedef değişkenini diğer bağımlı değişkenler kullanılarak tahmin etmektir. Bu kısımda k-ortalamalar (k-means) ve k-medoidler (k-medoids) hata metrikleri açısından performansları karşılaştırılmıştır. Analize başlamadan önce analiz için yüklenecek R kütüphaneleri verelim. Ardından keşifsel veri analizi (EDA) ile veri setini tanıyalım.

Yüklenecek kütüphaneler

kütüphaneler = c("dplyr","tibble","tidyr","ggplot2","formattable","readr","readxl","xlsx", "pastecs","randomForest", "aod", "fpc", "DescTools","factoextra","dendextend", "viridis","ggpurr","psych","writexl","ggfortify", "caret","cluster", "yardstick","MASS")

sapply(kütüphaneler, require, character.only = TRUE)

Veri setinin xlsx dosyasına yazdırılması

İhtiyaç duymanız halinde fonksiyonu ile birlikte yeniden kodlanan veri seti aşağıdaki kod yardımıyla xlsx uzantılı olarak excel dosyasına yazdırılmıştır.

#veri setinin xlsx dosyasına yazdırılması
write_xlsx(df1, "veriseti.xlsx")

Yukarıdaki R kod bloğunun çalıştırılması ile edilen veri seti dosyası xlsx uzantılı olarak aşağıda verilmiştir.

Veri setindeki değişkenlerin tanımlayıcı istatistikleri

df1<-iris

ti<-describe(iris[,-5])
formattable(tibble(Değişken=names(df1[,-5]), Aralık=ti$range, Ort=ti$mean, Medyan=ti$median, Ssapma=ti$sd, Carpıklık=ti$skew, Basıklık=ti$kurtosis) %>% mutate_if(is.numeric, round, 1))

#iris bitki türüne göre tanımlayıcı istatistikler
describe.by(df1, df1$Species)

formattable(head(df1,10))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tanımlayıcı istatistikler aşağıdaki tabloda verilmiştir.

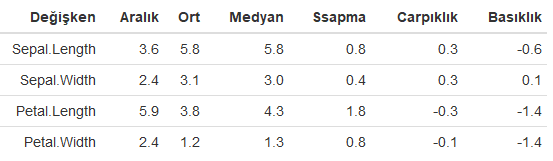
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen iris bitkisi türlerine göre tanımlayıcı istatistikler detaylı bir şekilde aşağıdaki tabloda verilmiştir.

Descriptive statistics by group 
group: setosa
             vars  n mean   sd median trimmed  mad min max range skew
Sepal.Length    1 50 5.01 0.35    5.0    5.00 0.30 4.3 5.8   1.5 0.11
Sepal.Width     2 50 3.43 0.38    3.4    3.42 0.37 2.3 4.4   2.1 0.04
Petal.Length    3 50 1.46 0.17    1.5    1.46 0.15 1.0 1.9   0.9 0.10
Petal.Width     4 50 0.25 0.11    0.2    0.24 0.00 0.1 0.6   0.5 1.18
Species*        5 50 1.00 0.00    1.0    1.00 0.00 1.0 1.0   0.0  NaN
             kurtosis   se
Sepal.Length    -0.45 0.05
Sepal.Width      0.60 0.05
Petal.Length     0.65 0.02
Petal.Width      1.26 0.01
Species*          NaN 0.00
--------------------------------------------------------- 
group: versicolor
             vars  n mean   sd median trimmed  mad min max range  skew
Sepal.Length    1 50 5.94 0.52   5.90    5.94 0.52 4.9 7.0   2.1  0.10
Sepal.Width     2 50 2.77 0.31   2.80    2.78 0.30 2.0 3.4   1.4 -0.34
Petal.Length    3 50 4.26 0.47   4.35    4.29 0.52 3.0 5.1   2.1 -0.57
Petal.Width     4 50 1.33 0.20   1.30    1.32 0.22 1.0 1.8   0.8 -0.03
Species*        5 50 2.00 0.00   2.00    2.00 0.00 2.0 2.0   0.0   NaN
             kurtosis   se
Sepal.Length    -0.69 0.07
Sepal.Width     -0.55 0.04
Petal.Length    -0.19 0.07
Petal.Width     -0.59 0.03
Species*          NaN 0.00
--------------------------------------------------------- 
group: virginica
             vars  n mean   sd median trimmed  mad min max range  skew
Sepal.Length    1 50 6.59 0.64   6.50    6.57 0.59 4.9 7.9   3.0  0.11
Sepal.Width     2 50 2.97 0.32   3.00    2.96 0.30 2.2 3.8   1.6  0.34
Petal.Length    3 50 5.55 0.55   5.55    5.51 0.67 4.5 6.9   2.4  0.52
Petal.Width     4 50 2.03 0.27   2.00    2.03 0.30 1.4 2.5   1.1 -0.12
Species*        5 50 3.00 0.00   3.00    3.00 0.00 3.0 3.0   0.0   NaN
             kurtosis   se
Sepal.Length    -0.20 0.09
Sepal.Width      0.38 0.05
Petal.Length    -0.37 0.08
Petal.Width     -0.75 0.04
Species*          NaN 0.00

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen veri setinin ilk 10 satırı aşağıda verilmiştir.

Veri setindeki değişkenlerin özellikleri

str(df1)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki değişkenlerin veri tipi ve faktör (kategori) seviyeleri aşağıda verilmiştir.

'data.frame':	150 obs. of  5 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

Veri setindeki eksik gözlemlerin (NAs)’nin tespiti

sapply(df1, function(x) sum(is.na(x)))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen çıktı aşağıda verilmiştir. Veri setinde eksik gözlem (missing data) bulunmamaktadır.

 Sepal.Length  Sepal.Width Petal.Length  Petal.Width      Species 
           0            0            0            0            0

Model 1: K Ortalamalar (K Means) Metodu

1 nolu modelin oluşturulması

set.seed(1923)
sonuc <- kmeans(df1[,-5], 3)
sonuc

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen model sonuçları aşağıda verilmiştir.

K-means clustering with 3 clusters of sizes 21, 33, 96

Cluster means:
  Sepal.Length Sepal.Width Petal.Length Petal.Width
1     4.738095    2.904762     1.790476   0.3523810
2     5.175758    3.624242     1.472727   0.2727273
3     6.314583    2.895833     4.973958   1.7031250

Clustering vector:
  [1] 2 1 1 1 2 2 2 2 1 1 2 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 1 1 2 2 2 1 2
 [37] 2 2 1 2 2 1 1 2 2 1 2 1 2 2 3 3 3 3 3 3 3 1 3 3 1 3 3 3 3 3 3 3 3 3 3 3
 [73] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3 3 3 3 1 3 3 3 3 3 3 3 3 3
[109] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[145] 3 3 3 3 3 3

Within cluster sum of squares by cluster:
[1]  17.669524   6.432121 118.651875
 (between_SS / total_SS =  79.0 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"    
[5] "tot.withinss" "betweenss"    "size"         "iter"        
[9] "ifault"     

Karışıklık matrisi (confusion matrix)’nin oluşturulması

Karışıklık matrisi kurulan model ile tahmin edilen hedef değişken bulgularını gözlemlenen hedef değişken bulguları ile karşılaştırır. Bu matris bir nevi sınıflandırma tablosu olup, gerçekleşen sınıflandırma bulguları ile tahmin edilen sınıflandırma bulgularının frekansı (n)’nı verir.

karsilastirma<-tibble(Küme=ifelse(sonuc$cluster==1, "setosa",ifelse(sonuc$cluster==2, "versicolor", "virginica")), Tahmin=df1$Species)%>% group_by(Küme, Tahmin) %>% summarise(Sayi=n()) 
karsilastirma %>% spread(Tahmin, Sayi, fill = 0)

#alternatif

karsilastirmak<-tibble(Gercek=ifelse(sonuc$cluster==1, "setosa",ifelse(sonuc$cluster==2, "versicolor", "virginica")), Tahmin=df1$Species)%>% mutate_if(is.character, as.factor)
cm <- karsilastirmak %>%
  conf_mat(Tahmin, Gercek)
cm
#karışıklık matriks (confusion matrix) grafiği
autoplot(cm, type = "heatmap

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisi aşağıda tabloda verilmiştir.

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisinin grafiği ise aşağıda verilmiştir.

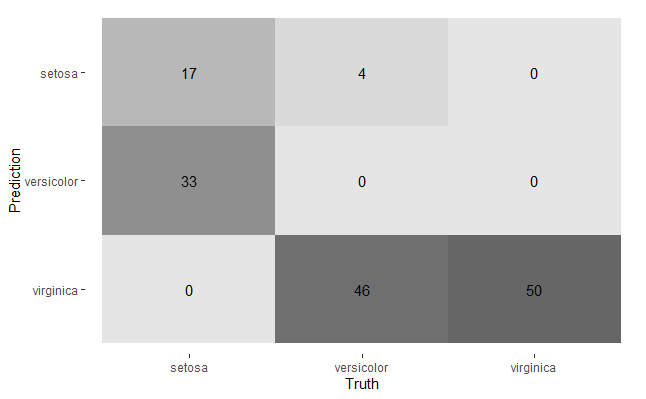
Hata metrikleri

Kurulan 1 nolu modele ait hata parametrelerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.

confusionMatrix(karsilastirmak$Gercek, karsilastirmak$Tahmin)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen hata metrikleri bir bütün olarak hata metrikleri ile birlikte aşağıda verilmiştir. K-ortalamalar metoduyla kurulan model iris bitki türlerini yaklaşık % 45 doğruluk (accuracy) oranı ile tahmin etmektedir. Uyumu gösteren Kappa katsayısı ise bu modelde 0,17 olup, tahmin edilen iris bitki türleri ile gözlemlenen bitki türleri arasında uyumun çok düşük olduğu göstermektedir. Bu bulgu aynı zamanda doğruluk oranını da doğrular niteliktedir.

Confusion Matrix and Statistics

            Reference
Prediction   setosa versicolor virginica
  setosa         17          4         0
  versicolor     33          0         0
  virginica       0         46        50

Overall Statistics
                                          
               Accuracy : 0.4467          
                 95% CI : (0.3655, 0.5299)
    No Information Rate : 0.3333          
    P-Value [Acc > NIR] : 0.002528        
                                          
                  Kappa : 0.17            
                                          
 Mcnemar's Test P-Value : NA              

Statistics by Class:

                     Class: setosa Class: versicolor Class: virginica
Sensitivity                 0.3400            0.0000           1.0000
Specificity                 0.9600            0.6700           0.5400
Pos Pred Value              0.8095            0.0000           0.5208
Neg Pred Value              0.7442            0.5726           1.0000
Prevalence                  0.3333            0.3333           0.3333
Detection Rate              0.1133            0.0000           0.3333
Detection Prevalence        0.1400            0.2200           0.6400
Balanced Accuracy           0.6500            0.3350           0.7700

Gözlem ve tahmin sınıflandırma sonuçlarının xlsx dosyasına yazdırılması

kortalama<-tibble(Gözlem=ifelse(sonuc$cluster==1, "setosa",ifelse(sonuc$cluster==2, "versicolor", "virginica")), Tahmin=df1$Species)
write_xlsx(kortalama, "kortalama.xlsx")

Yukarıdaki R kod bloğunun çalıştırılmasıyla elde edilen tahmin sonuçları gözlem değerleriyle birlikte xlsx uzantılı olarak aşağıdan indirebilirsiniz.

Kümelerin grafikle gösterilmesi

set.seed(1923)
sonuc <- kmeans(df1[,-5], 3)
fviz_cluster(sonuc, df1[, -5], ellipse.type = "norm")

Yukarıdaki R kod bloğunun yazılmasından sonra elde k-ortalamalar küme grafiği aşağıda verilmiştir. Kümelerin çok iç içe girdiği birbirinden ayrışmadığı görülmektedir. Bu durum sınıflandırmanın çok da iyi olmadığını göstermektedir.

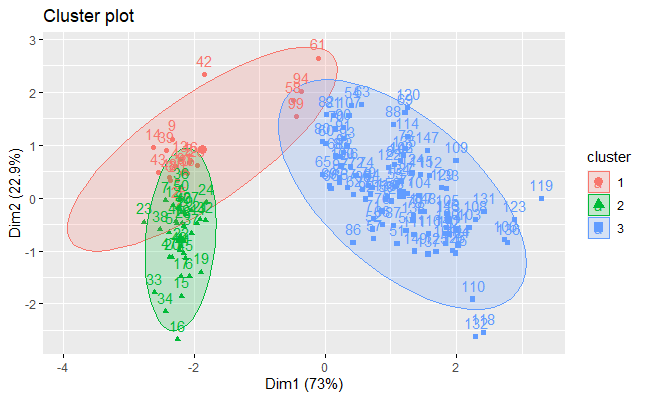
Model 2: K-Medoidler (K Medoids) Metodu

2 nolu modelin oluşturulması

set.seed(1900)
psonuc <- pamk(df1[,-5],3)
psonuc

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen model sonuçları aşağıda verilmiştir.

$pamobject
Medoids:
      ID Sepal.Length Sepal.Width Petal.Length Petal.Width
[1,]   8          5.0         3.4          1.5         0.2
[2,]  79          6.0         2.9          4.5         1.5
[3,] 113          6.8         3.0          5.5         2.1
Clustering vector:
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [73] 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3
[109] 3 3 3 3 3 2 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3
[145] 3 3 2 3 3 2
Objective function:
    build      swap 
0.6709391 0.6542077 

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
 [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"      

$nc
[1] 3

$crit
[1] 0.000000 0.000000 0.552819

Karışıklık matrisi (confusion matrix)’nin oluşturulması

karsilastirma<-tibble(Küme=ifelse(psonuc$pamobject$clustering==1, "setosa",ifelse(psonuc$pamobject$clustering==2, "versicolor", "virginica")), Tahmin=df1$Species)%>% group_by(Küme, Tahmin) %>% summarise(Sayi=n()) 
karsilastirma<-karsilastirma %>% spread(Tahmin, Sayi, fill = 0)
formattable(karsilastirma)

#alternatif

karsilastirmat<-tibble(Gercek=ifelse(psonuc$pamobject$clustering==1, "setosa",ifelse(psonuc$pamobject$clustering==2, "versicolor", "virginica")), Tahmin=df1$Species)%>% mutate_if(is.character, as.factor)
cm <- karsilastirmat %>%
  conf_mat(Tahmin, Gercek)
cm
#karışıklık matriks (confusion matrix) grafiği
autoplot(cm, type = "heatmap")

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisi aşağıda tabloda verilmiştir.

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisinin grafiği ise aşağıda verilmiştir.

Hata metrikleri

Kurulan 2 nolu modele ait hata metriklerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.

confusionMatrix(karsilastirmak$Gercek, karsilastirmak$Tahmin)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen hata metrikleri bir bütün olarak hata metrikleri ile birlikte aşağıda verilmiştir. K-medoidler metoduyla kurulan model iris bitki türlerini % 89 doğruluk (accuracy) oranı ile tahmin etmektedir. Uyumu gösteren Kappa katsayısı ise bu modelde 0,84 olup, tahmin edilen iris bitki türleri ile gözlemlenen bitki türleri arasında uyumun çok yüksek olduğu göstermektedir. Bu bulgu aynı zamanda yüksek doğruluk oranını da doğrular niteliktedir.

            Truth
Prediction   setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48        14
  virginica       0          2        36
Confusion Matrix and Statistics

            Reference
Prediction   setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48        14
  virginica       0          2        36

Overall Statistics
                                          
               Accuracy : 0.8933          
                 95% CI : (0.8326, 0.9378)
    No Information Rate : 0.3333          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.84            
                                          
 Mcnemar's Test P-Value : NA              

Statistics by Class:

                     Class: setosa Class: versicolor Class: virginica
Sensitivity                 1.0000            0.9600           0.7200
Specificity                 1.0000            0.8600           0.9800
Pos Pred Value              1.0000            0.7742           0.9474
Neg Pred Value              1.0000            0.9773           0.8750
Prevalence                  0.3333            0.3333           0.3333
Detection Rate              0.3333            0.3200           0.2400
Detection Prevalence        0.3333            0.4133           0.2533
Balanced Accuracy           1.0000            0.9100           0.8500

Gözlem ve tahmin sınıflandırma sonuçlarının xlsx dosyasına yazdırılması

kmedoidler<-tibble(Gözlem=ifelse(psonuc$pamobject$clustering==1, "setosa",ifelse(psonuc$pamobject$clustering==2, "versicolor", "virginica")), Tahmin=df1$Species)
write_xlsx(kmedoidler, "kmedoidler.xlsx")

Yukarıdaki R kod bloğunun çalıştırılmasıyla elde edilen tahmin sonuçları gözlem değerleriyle birlikte xlsx uzantılı olarak aşağıdan indirebilirsiniz.

Kümelerin grafikle gösterilmesi

set.seed(1900)
psonuc <- pam(df1[,-5],3)
fviz_cluster(psonuc, geom = "point", ellipse.type = "norm")

Yukarıdaki R kod bloğunun yazılmasından sonra elde edilen k-medoidler küme grafiği aşağıda verilmiştir.

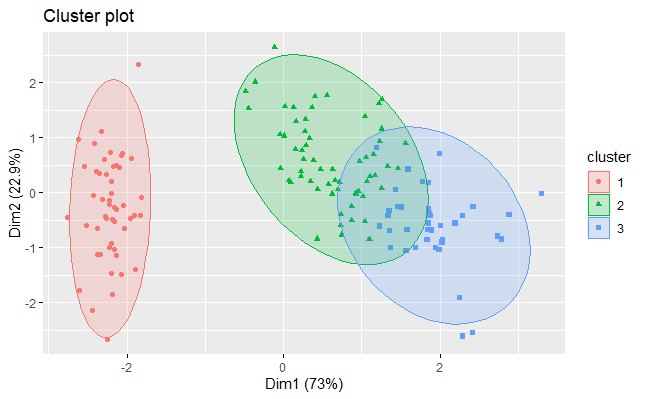
Sonuç

Bu çalışmada sınıflandırma (classification) probleminin çözümüne yönelik küme analiz metodlarından k-ortalama ve k-medoidler kullanılarak ayrıntılı karşılaştırmalı deneysel bir çalışma yapılmıştır. Ortaya konulan bulgular, sınıflandırma probleminin k-medoidler tarafından başarılı bir şekilde, diğer bir ifadeyle yüksek bir doğruluk oranıyla çözüme kavuşturulduğu görülmektedir.

Her iki yöntem sınıflandırma hata metrikleri açısından karşılaştırıldığında öne çıkan bulgular şöyledir: K-medoidler bağımlı değişken olan “species” değişkenini çok daha iyi tahmin etmektedir. Bu yöntemde doğruluk (accuracy) oranı % 89,3 düzeyindeyken, k-ortalamalar yönteminde bu oran yaklaşık % 45 düzeyinde kalmıştır. Diğer bir ifadeyle k-medoidler yöntemi bağımlı değişkeni k-ortalamalar yönteminden neredeyse iki kat daha iyi tahmin etmektedir. Elde edilen sonuçların uyumunu gösteren Kappa katsayısı da bunun iyi bir göstergesidir. Yüksek katsayı yüksek uyumu gösterir ve bu istenen bir durumdur. K-ortalamalar yönteminden elde Kappa katsayısı çok düşük (0,17) iken, bu katsayı k-medoidler yönteminde çok yüksek (0,84)’tir.

Yapılan bu çalışma ile özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına önemli bir katkı sunulacağı düşünülmektedir.

Faydalı olması ve farkındalık oluşturması dileğiyle.

Bilimle ve teknolojiyle kalınız.

Saygılarımla.

Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.

Note: It can not be cited or copied without referencing.

Yararlanılan Kaynaklar