Introduction
The aim of this study is to predict the birth rate from the data sets of United States Department of Agriculture (Economic Research Service) and the United States’ Census Bureau using different analysis methods. The methods used in the regression problem are linear regression (LM), artificial neural network (ANN), radial, and linear support vector machines (SVMs).
SVMs are dealt with in the supervised learning class of artificial intelligence (AI) and machine learning (ML). In this analysis, ANN method can be considered as DNN (Deep Neural Network) because it has ANN architecture with more than one hidden layer. In the other hand, DNN can be evaluated in the supervised learning class of AI, and in in the field of deep learning (DL).
The results indicate that when Mean Square Error (MSE) and Mean Absolute Error (MAE) error types are compared, the SVM method including the radial basis parameter predicts the birth rates better than the other methods.
Sources of data sets utilized in analysis are given below
- https://www.ers.usda.gov/data-products/county-level-data-sets/download-data/
- https://www.census.gov/data/tables/time-series/demo/popest/2010s-state-detail.html
- https://www.census.gov/data/tables/time-series/demo/health-insurance/acs-hi.2017.htmlNA (Not Available) values are removed from data set.
Data set is consisted of 3141 observations of 11 variables. The variables selected in the analysis are listed below.
- Birth_Rate (Target Variable or Dependent Variable)
- Death_Rate
- Net_Migration_Rate
- Unemployment_Rate
- less_high_school
- high_school
- associate
- bachelor_or_higher
- Poverty_Percent
- Marriage_Rate
- Percent_Uninsured
The procedures and methods used in the analysis are explained step by step in the next sections.
Loading libraries
rm(list=ls())
lapply(c("xlsx","dplyr", "tibble", "tidyr", "ggplot2", "GGally","NeuralNetTools" ,"neuralnet", "formattable", "performanceEstimation", "e1071", "DMwR", "caret"), require, character.only = TRUE)
Loading data set
df <- read.xlsx('data_end_2017.xlsx', sheetName='data')
Defining variables in Tibble and data cleaning
df1<-tibble(Birth_Rate=round(df$Birth_Rate,1), Death_Rate=round(df$Death_Rate, 1),Net_Migration_Rate=round(df$Net_Migration_Rate, 1), Unemployment_Rate=df$Unemployment_Rate,less_high_school=df$V5, high_school=df$V6, associate=df$V7, bachelor_or_higher=df$V8, Poverty_Percent=df$Poverty_Percent, Marriage_Rate=round(df$Marriage_Rate, 1), Percent_Uninsured=df$Percent_Uninsured)
formattable(tibble(ID=1:11, Variables=names(df1))) #Names of variables
str(df1)#3142 observations of 11 variables
df1<-df1 %>% drop_na()#Removing NA (Not Available) values from data set
str(df1)##3141 observations of 11 variables
dim(df1)# Dimensions of data sets: 3141 11
summary(df1)
head(df1)
Names of variables

Data types of variables and number of observations after removing NA values
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 3141 obs. of 11 variables:
$ Birth_Rate : num 11.9 10.9 10.7 12 11.5 12.2 11.7 11.4 10.8 8.4 ...
$ Death_Rate : num 9.3 10.1 11.7 9.7 12.4 11.3 13.1 12.6 13.6 13.8 ...
$ Net_Migration_Rate: num 1 22.5 -25 -3.1 6.4 -21 -5.2 -1.8 2.5 6.9 ...
$ Unemployment_Rate : num 3.9 4.1 5.8 4.4 4 4.9 5.5 5 4.1 4.1 ...
$ less_high_school : num 12.3 9.8 26.9 17.9 20.2 28.6 18.9 16.8 19.1 20.5 ...
$ high_school : num 33.6 27.8 35.5 43.9 32.3 36.6 40.4 32.2 38.4 38.2 ...
$ associate : num 29.1 31.7 25.5 25 34.4 21.4 24.5 33.1 29.1 28.9 ...
$ bachelor_or_higher: num 25 30.7 12 13.2 13.1 13.4 16.1 17.9 13.3 12.5 ...
$ Poverty_Percent : num 13.4 10.1 33.4 20.2 12.8 34.4 21.3 17.7 18.2 17.2 ...
$ Marriage_Rate : num 7 7 7 7 7 7 7 7 7 7 ...
$ Percent_Uninsured : num 16 16 16 16 16 16 16 16 16 16 ...
Descriptive statistics of variables
Birth_Rate Death_Rate Net_Migration_Rate Unemployment_Rate
Min. : 0.00 Min. : 1.20 Min. :-68.3000 Min. : 1.500
1st Qu.: 9.90 1st Qu.: 8.60 1st Qu.: -5.4000 1st Qu.: 3.500
Median :11.30 Median :10.40 Median : 0.5000 Median : 4.300
Mean :11.38 Mean :10.27 Mean : 0.9654 Mean : 4.598
3rd Qu.:12.60 3rd Qu.:12.10 3rd Qu.: 7.5000 3rd Qu.: 5.300
Max. :28.80 Max. :21.30 Max. :150.2000 Max. :19.600
less_high_school high_school associate bachelor_or_higher
Min. : 1.10 Min. : 7.30 Min. : 8.80 Min. : 4.70
1st Qu.: 9.00 1st Qu.:30.00 1st Qu.:27.00 1st Qu.:14.70
Median :12.40 Median :34.80 Median :30.60 Median :19.00
Mean :13.81 Mean :34.42 Mean :30.56 Mean :21.21
3rd Qu.:17.70 3rd Qu.:39.40 3rd Qu.:34.00 3rd Qu.:25.30
Max. :58.70 Max. :54.90 Max. :46.70 Max. :78.10
Poverty_Percent Marriage_Rate Percent_Uninsured
Min. : 3.00 Min. : 5.50 Min. : 3.00
1st Qu.:10.90 1st Qu.: 6.00 1st Qu.:11.00
Median :14.40 Median : 6.80 Median :15.00
Mean :15.38 Mean : 6.86 Mean :18.66
3rd Qu.:18.40 3rd Qu.: 7.10 3rd Qu.:23.00
Max. :56.70 Max. :28.60 Max. :48.00
Scatter pair plots of variables: Base mode
pairs(df1[,1:4], pch = 18, cex = 1, col=as.factor(1:3), lower.panel=NULL)
pairs(df1[,c(1,5:8)], pch = 18, cex = 1, col=as.factor(1:3), lower.panel=NULL)
pairs(df1[,c(1,9:11)], pch = 18, cex = 1, col=as.factor(1:2), lower.panel=NULL)
Plot 1: Scatter pair plots of variables: Base mode
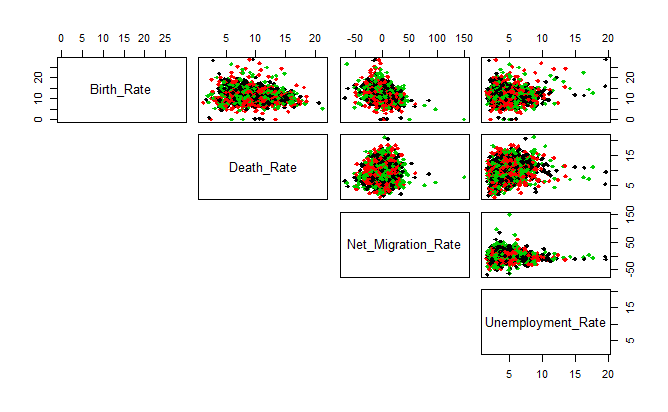
Plot 2: Scatter pair plots of variables: Base mode

Plot 3: Scatter pair plots of variables: Base mode
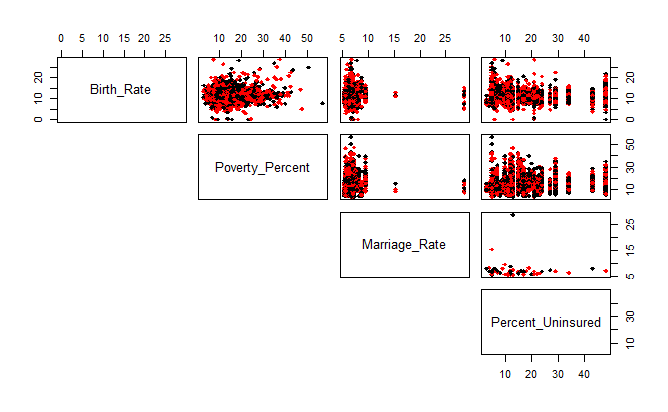
Scatter pair plots and correlation coefficients: Ggpairs mode
ggpairs(df1[,1:4])
ggpairs(df1[,c(1,5:8)])
ggpairs(df1[,c(1,9:11)])
Plot 1: Scatter pair plots and correlation coefficients: Ggpairs mode

Plot 2: Scatter pair plots and correlation coefficients: Ggpairs mode
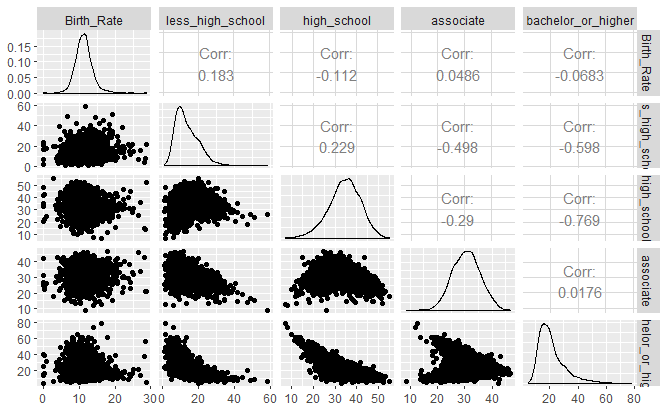
Plot 3: Scatter pair plots and correlation coefficients: Ggpairs mode

Splitting data set into training and test sets
Data set is splitted into training (70%) and test (30%) sets by simple random sampling (SRS) without replacement.
set.seed(1150)
n=NROW(df1)
SRS<-sample(sample(1:n, size = round(0.7*n), replace=FALSE))
training<-df1[SRS,]
test<-df1[-SRS, ]
Building Linear Model (LM) and Predicting
lm.fit <- glm(Birth_Rate~., data=training)
summary(lm.fit)
pr.lm <- predict(lm.fit,test)
Summary of LM
Call:
glm(formula = Birth_Rate ~ ., data = training)
Deviance Residuals:
Min 1Q Median 3Q Max
-12.6431 -1.2701 0.0494 1.2338 17.5226
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.210336 86.506626 -0.014 0.989
Death_Rate -0.196533 0.022653 -8.676 < 2e-16 ***
Net_Migration_Rate -0.040544 0.004030 -10.061 < 2e-16 ***
Unemployment_Rate -0.069103 0.036281 -1.905 0.057 .
less_high_school 0.238640 0.864714 0.276 0.783
high_school 0.090654 0.865317 0.105 0.917
associate 0.201731 0.865124 0.233 0.816
bachelor_or_higher 0.123188 0.865118 0.142 0.887
Poverty_Percent 0.019001 0.012121 1.568 0.117
Marriage_Rate -0.012984 0.031243 -0.416 0.678
Percent_Uninsured -0.022913 0.004762 -4.812 1.6e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for gaussian family taken to be 5.620194)
Null deviance: 14742 on 2198 degrees of freedom
Residual deviance: 12297 on 2188 degrees of freedom
AIC: 10050
Number of Fisher Scoring iterations: 2
Building Artificial Neural Network (ANN) Model
nn<- neuralnet(Birth_Rate ~ Death_Rate + Unemployment_Rate + Net_Migration_Rate+less_high_school+high_school+high_school+associate+bachelor_or_higher+Poverty_Percent+Marriage_Rate+Percent_Uninsured, training, hidden=c(3,2), linear.output=T, threshold=0.01)
summary(nn)
nn$result.matrix#Generating the error of the neural network model
plot(nn)#ANN Architecture
plotnet(nn, cex_val = 1, alpha_val = 1, prune_lty = "dashed")#NN Architecture
Summary of ANN
Length Class Mode
call 6 -none- call
response 2199 -none- numeric
covariate 21990 -none- numeric
model.list 2 -none- list
err.fct 1 -none- function
act.fct 1 -none- function
linear.output 1 -none- logical
data 11 data.frame list
exclude 0 -none- NULL
net.result 1 -none- list
weights 1 -none- list
generalized.weights 1 -none- list
startweights 1 -none- list
result.matrix 47 -none- numeric
Generating error of ANN model
error 7.190738e+03
reached.threshold 9.953213e-03
steps 5.492700e+04
Intercept.to.1layhid1 -1.420848e+00
Death_Rate.to.1layhid1 1.729804e+00
Unemployment_Rate.to.1layhid1 3.007492e-01
Net_Migration_Rate.to.1layhid1 -4.764154e-01
less_high_school.to.1layhid1 8.628385e-01
high_school.to.1layhid1 1.072833e+00
associate.to.1layhid1 1.401955e+00
bachelor_or_higher.to.1layhid1 -1.783482e-01
Poverty_Percent.to.1layhid1 -9.234006e-01
Marriage_Rate.to.1layhid1 -4.927336e-01
Percent_Uninsured.to.1layhid1 2.478482e+00
Intercept.to.1layhid2 2.723703e-01
Death_Rate.to.1layhid2 -1.700317e+00
Unemployment_Rate.to.1layhid2 5.703225e-01
Net_Migration_Rate.to.1layhid2 -2.078499e+00
less_high_school.to.1layhid2 -1.010006e+00
high_school.to.1layhid2 1.714122e+00
associate.to.1layhid2 4.837800e-01
bachelor_or_higher.to.1layhid2 1.039985e+00
Poverty_Percent.to.1layhid2 9.512370e-01
Marriage_Rate.to.1layhid2 -5.561333e-01
Percent_Uninsured.to.1layhid2 -3.077538e-01
Intercept.to.1layhid3 -1.322371e+00
Death_Rate.to.1layhid3 -7.556517e-01
Unemployment_Rate.to.1layhid3 4.942474e-01
Net_Migration_Rate.to.1layhid3 -3.532218e-01
less_high_school.to.1layhid3 1.597219e-01
high_school.to.1layhid3 5.478689e-01
associate.to.1layhid3 1.378378e+00
bachelor_or_higher.to.1layhid3 1.820102e-01
Poverty_Percent.to.1layhid3 1.701603e+00
Marriage_Rate.to.1layhid3 -5.974305e-02
Percent_Uninsured.to.1layhid3 8.631418e-01
Intercept.to.2layhid1 -5.147527e+00
1layhid1.to.2layhid1 -6.029849e+00
1layhid2.to.2layhid1 1.672761e+02
1layhid3.to.2layhid1 -5.579418e+00
Intercept.to.2layhid2 1.244695e+01
1layhid1.to.2layhid2 1.278534e+01
1layhid2.to.2layhid2 1.912635e+00
1layhid3.to.2layhid2 1.174542e+01
Intercept.to.Birth_Rate 4.943155e+00
2layhid1.to.Birth_Rate 3.305572e+00
2layhid2.to.Birth_Rate 3.178053e+00
ANN architecture with two hidden layers

Importance levels of variables in ANN model
In the ANN model, importance levels of variables are calculated using “olden” function because of multiple hidden layers (hidden=c(3,2)), and given below.
olden(nn)+ theme(axis.text.x = element_text(angle = 90, hjust = 1))#Variable importance in ANNs including multiple hidden layers
Importance levels of variables in ANN model
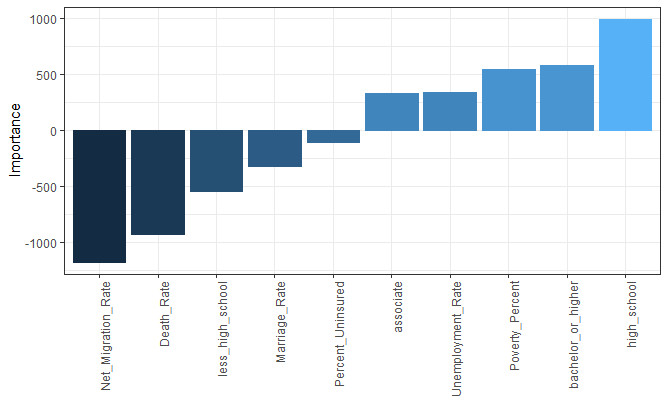
Predicting Birth Rate using ANN
predict_nn <- compute(nn,test[,2:11])
Building SVM (Support Vector Machine) model with Radial Basis parameter, and Prediction
model1 <- svm(Birth_Rate~ ., training, kernel="radial", cost=1, epsilon=0.1, gamma=0.1)
summary(model1)
pred1 <- predict(model1, test)
Summary of SVM with Radial Basis parameter
Call:
svm(formula = Birth_Rate ~ ., data = training, kernel = "radial",
cost = 1, epsilon = 0.1, gamma = 0.1)
Parameters:
SVM-Type: eps-regression
SVM-Kernel: radial
cost: 1
gamma: 0.1
epsilon: 0.1
Number of Support Vectors: 1902
Building SVM (Support Vector Machine) model with Linear parameter, and Prediction
model1 <- svm(Birth_Rate~ ., training, kernel="linear")
pred2 <- predict(model1, test)
summary(model1)
Summary of SVM with Linear parameter
Call:
svm(formula = Birth_Rate ~ ., data = training, kernel = "linear")
Parameters:
SVM-Type: eps-regression
SVM-Kernel: linear
cost: 1
gamma: 0.1
epsilon: 0.1
Number of Support Vectors: 1929
Validation Tests by Methods
1.Cross Validation for LM
r <- performanceEstimation(
PredTask(Birth_Rate ~ .,df1),
workflowVariants(learner = "lm",
learner.pars = list(se = c(0, 0.25, 0.5, 1, 2))),
EstimationTask(metrics = c("mse", "mae"),
method = CV(nReps = 3, nFolds = 10)))
rankWorkflows(r, top = 1)
getWorkflow("lm.v1", r)# AVG MSE: 5.61858 and AVG MAE:1.673429
plot(r)
Average MSE, and average MAE for LM model
$df1.Birth_Rate
$df1.Birth_Rate$mse
Workflow Estimate
1 lm.v1 5.613821
$df1.Birth_Rate$mae
Workflow Estimate
1 lm.v1 1.674253
Plotting MSE and MAE values for LM model
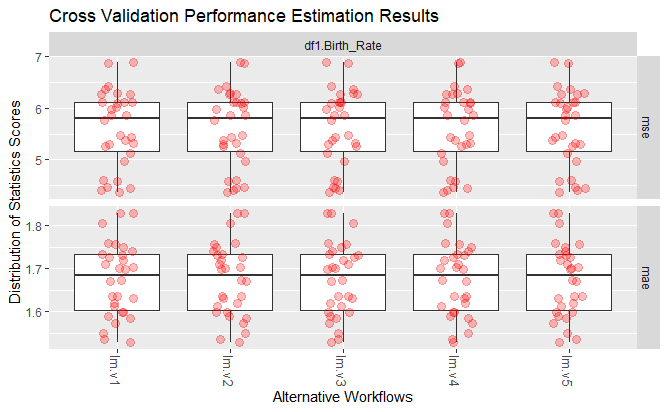
2. Cross Validation for ANN
#Repeated k-fold Cross Validation
train_control <- trainControl(method="repeatedcv", number=10, repeats=3)
# Train the model
model <- train(Birth_Rate~., data=df1, trControl=train_control, method="nnet")
print(model)
Average MAE for ANN model
It is used Repeated k-fold Cross Validation (NN) as validation test in package “caret” insead of “performanceEstimation” package.
initial value 403331.122522
final value 359465.140000
converged
Neural Network
3141 samples
10 predictor
No pre-processing
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 2827, 2827, 2826, 2827, 2828, 2827, ...
Resampling results across tuning parameters:
size decay RMSE Rsquared MAE
1 0e+00 10.69727 NaN 10.38151
1 1e-04 10.69727 0.002990157 10.38151
1 1e-01 10.69729 0.018808431 10.38152
3 0e+00 10.69727 NaN 10.38151
3 1e-04 10.69727 0.024056622 10.38151
3 1e-01 10.69728 0.017597580 10.38152
5 0e+00 10.69727 NaN 10.38151
5 1e-04 10.69727 0.011161407 10.38151
5 1e-01 10.69728 0.022457815 10.38151
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were size = 1 and decay = 0.
3. Cross Validation for SVM (Support Vector Machine) with Radial Basis parameter
pr1 <- performanceEstimation(
PredTask(Birth_Rate ~ .,df1),
workflowVariants(learner="svm",
learner.pars=list(kernel="radial",cost=1, epsilon=0.1, gamma=0.1)),
EstimationTask(metrics = c("mse", "mae"),
method = CV(nReps = 3, nFolds = 10)))
summary(pr1)# AVG MSE:5.0181919 and AVG MAE:1.52361665
rankWorkflows(pr1, top = 1)
getWorkflow("svm", pr1)
plot(pr1)
Average MSE, and average MAE for SVM (Support Vector Machine) with Radial Basis parameter
-> Task: df1.Birth_Rate
*Workflow: svm
mse mae
avg 5.0237890 1.52349784
std 0.7941622 0.08445783
med 4.8739686 1.51075518
iqr 0.9747409 0.10690584
min 3.5181964 1.37328251
max 6.4726952 1.71792661
invalid 0.0000000 0.00000000
$df1.Birth_Rate
$df1.Birth_Rate$mse
Workflow Estimate
1 svm 5.023789
$df1.Birth_Rate$mae
Workflow Estimate
1 svm 1.523498
Workflow Object:
Workflow ID :: svm
Workflow Function :: standardWF
Parameter values:
learner.pars -> kernel=radial cost=1 epsilon=0.1 gamma=0.1
learner -> svm
Plotting MSE and MAE values for SVM (Support Vector Machine) with Radial Basis parameter

4. Cross Validation for SVM (Support Vector Machine) with Linear parameter
pr1 <- performanceEstimation(
PredTask(Birth_Rate ~ .,df1),
workflowVariants(learner="svm",
learner.pars=list(kernel="linear")),
EstimationTask(metrics = c("mse", "mae"),
method = CV(nReps = 3, nFolds = 10)))
summary(pr1)# AVG MSE:5.671183 and AVE MAE:1.6563516
rankWorkflows(pr1, top = 1)
getWorkflow("svm", pr1)
plot(pr1)
Average MSE, and average MAE for SVM (Support Vector Machine) with Linear parameter
##### PERFORMANCE ESTIMATION USING CROSS VALIDATION #####
** PREDICTIVE TASK :: df1.Birth_Rate
++ MODEL/WORKFLOW :: svm
Task for estimating mse,mae using
3 x 10 - Fold Cross Validation
Run with seed = 1234
Iteration :******************************
== Summary of a Cross Validation Performance Estimation Experiment ==
Task for estimating mse,mae using
3 x 10 - Fold Cross Validation
Run with seed = 1234
* Predictive Tasks :: df1.Birth_Rate
* Workflows :: svm
-> Task: df1.Birth_Rate
*Workflow: svm
mse mae
avg 5.6742841 1.65745175
std 0.8087646 0.08828428
med 5.7814504 1.66599466
iqr 1.0277489 0.12239844
min 4.1506266 1.51514278
max 7.1174248 1.81856657
invalid 0.0000000 0.00000000
$df1.Birth_Rate
$df1.Birth_Rate$mse
Workflow Estimate
1 svm 5.674284
$df1.Birth_Rate$mae
Workflow Estimate
1 svm 1.657452
Workflow Object:
Workflow ID :: svm
Workflow Function :: standardWF
Parameter values:
learner.pars -> kernel=linear
learner -> svm
Plotting MSE and MAE values for SVM (Support Vector Machine) with Linear parameter
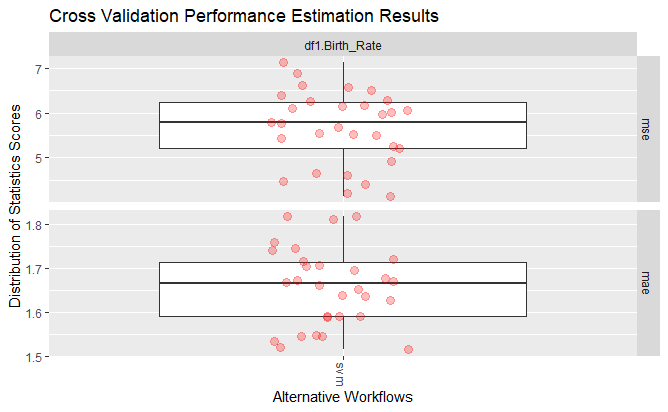
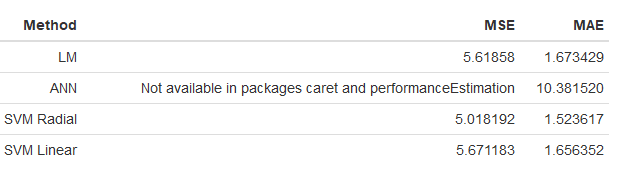
The models built were validated using “performanceEstimation” and “caret” packages. As validation test, Repetitive k-Fold cross validation test (nReps = 3) was used. The MAE and MSE results of the methods used are given in the table 1 below after being presented code block.
Method<-c("LM", "ANN", "SVM Radial", "SVM Linear")
MSE<-list(5.61858, "Not available in packages caret and performanceEstimation",5.0181919,5.671183)
MAE<-c(1.673429, 10.38152,1.52361665,1.6563516)
formattable(tibble(Method=Method, MSE=MSE, MAE=MAE))
Table 1: The MAE and MSE Results of the Methods by Validation Tests
Plotting the results of actual and predicted birth rates by methods
Visual comparison of performance of methods is conducted in terms of actual test values and predicted ones, and were shown below.
#ANN: Comparison of actual and predictive birth rates
results <- data.frame(actual = test$Birth_Rate, predictionNN = round(predict_nn$net.result,1))
#LM: Comparison of actual and predictive birth rates
results1 <- data.frame(actual = test$Birth_Rate, predictionLM = round(pr.lm,1))
#SVM with Radial Basis Parameter: Comparison of actual and predictive birth rates
results3 <- data.frame(actual = round(test$Birth_Rate,1), predictionSVMKernel = round(pred1,1))
#SVM with Linear Parameter: Comparison of actual and predictive birth rates
results4 <- data.frame(actual = round(test$Birth_Rate,1), predictionSVMLinear = round(pred2,1))
comp<-cbind(Birth_Rate=results[,1],NN=results[,2], LM=results1[, 2], SVMRadial=results3[, 2], SVMLinear=results4[, 2])
comparison<-formattable(as_tibble(comp))
plot(test$Birth_Rate,predict_nn$net.result,col='red',main='Real vs predicted NN',pch=18,cex=0.7, xlab="Birth Rate", ylab = "Prediction" )
points(test$Birth_Rate, pr.lm,col='blue',pch=18,cex=0.7)
points(test$Birth_Rate, comparison$SVMRadial,col='brown',pch=18,cex=0.7)
points(test$Birth_Rate, comparison$SVMLinear,col='green',pch=18,cex=0.7)
abline(0,1,lwd=2)
legend("topright",legend=c('NN','LM', 'SVMRadial','SVMLinear'),pch=18,col=c('red','blue', 'brown', 'green'))

Writing results containing actual and predicted birth rates by method into the file with “xlsx” extension
write.xlsx(comparison, file = "comparison_results.xlsx",
sheetName="results", append=TRUE)
The file called “comparison_results” actual and predicted birth rates by method can be downloaded from the link below.
Showing first ten findings containing actual and predicted values by method
After being presented code block, the first ten rows of actual and predicted birth rates by method used are given in Table 2.
formattable(head(comparison,10))
Table 2: The First Ten Findings Containing Actual and Predicted Birth Rates by Method

Conclusion
As can be seen from the validation test results in the Table 1 above, SVM including Radial Basis Parameter is the best method in terms of MAE and MSE values obtained. Therefore, it is recommended that SVM with Radial Basis Parameter can be used in prediction of birth rates.
Hope to be useful and raise awareness.
Note: It can not be cited or copied without referencing.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
References
- https://www.ers.usda.gov/data-products/county-level-data-sets/download-data/
- https://www.census.gov/data/tables/time-series/demo/popest/2010s-state-detail.html
- https://www.census.gov/data/tables/time-series/demo/health-insurance/acs-hi.2017.html
- https://www.r-project.org/
- https://datascienceplus.com/neuralnet-train-and-test-neural-networks-using-r/
- http://cs229.stanford.edu/notes/cs229-notes3.pdf
- http://www.cs.columbia.edu/~kathy/cs4701/documents/jason_svm_tutorial.pdf
- http://svms.org/tutorials/BurbidgeBuxton2001.pdf
- https://course.ccs.neu.edu/cs5100f11/resources/jakkula.pdf
- https://med.nyu.edu/chibi/sites/default/files/chibi/Final.pdf
- http://ijarcet.org/wp-content/uploads/IJARCET-VOL-1-ISSUE-10-185-189.pdf
- http://www.ijastnet.com/journals/Vol_7_No_2_June_2017/2.pdf
- https://www.demographic-research.org/volumes/vol20/25/20-25.pdf
- https://www.hindawi.com/journals/cmmm/2013/487179/
- http://www.cinc.org/Proceedings/2005/pdf/0247.pdf
- https://scialert.net/fulltext/?doi=jai.2016.33.38
- https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2894370
- https://www.ijeat.org/wp-content/uploads/papers/v9i1/A9386109119.pdf
- https://www.ijitee.org/wp-content/uploads/papers/v8i9S/I11460789S19.pdf
- https://biomedpharmajournal.org/vol11no3/emg-signal-analysis-for-diagnosis-of-muscular-dystrophy-using-wavelet-transform-svm-and-ann/
- https://canvas.harvard.edu/courses/12656/files/3151019/download?verifier=62k2w6mW3Glg0caFIRHfXACHlC0iS5JzwJTfTZZr&wrap=1
- https://scholar.harvard.edu/files/javierzazo/files/svms.pdf