Olasılık konusu öteden beri ilgimi çekmiş ve ara ara üzerine yoğunlaşma fırsatım olmuştur. Çoğu analiz yönteminin temelini oluşturan olasılık dağılımları da böyledir. İşin esasında olasılıkları dağılımları tam anlaşılmadan analiz yöntemleri ile istenilen sonuçların elde edilmesi tek başına bazıları için yeterli olsa da işin felsefesini anlamak açısından kesinlikle yetersizdir. Bu nedenle bu çalışmada öncelikle kesikli (disrete) ve sürekli (continous) dağılımlar başlıklar halinde verildikten sonra kesikli dağılım türlerinden biri olan Bernoulli dağılımı uygulama örnekleriyle ele alınarak somutlaştırılacaktır. Uygulama örnekleri R programlama dili kullanılarak adım adım yapılacaktır. Bazı yerlerde hem excel üzerinde de uygulama yapılarak R programlama dili bilmeyenler için de kolaylık sağlanacaktır.
Rastlantı ya da kesin olmayan olaylarla ilgilenen olasılık teorisi, rastlantı olaylarını belirli kurallara göre matematik disiplininde inceleyen bir bilim dalıdır. Burada, rastlantı olayından kasıt gerçekleşmesi şansa bağlı olan önceden bilinmeyen olaylardır.
İstatistikte ve makine öğrenmede, diğer bir deyişle veri biliminde sıklıkla kullanılan örneklem uzayına bağlı olarak olasılık fonksiyon türleri kesikli ve sürekli olmak üzere iki ana başlıkta ele alınmaktadır.
- Kesikli Olasılık Fonksiyonu: Olasılık fonksiyonlarından ilki olan kesikli olasılık fonksiyonu örneklem uzayından elde edilen sonlu veya sayılabilir sonsuz sayıda ayrık sonuçları içermektedir.
- Sürekli Olasılık Fonksiyonu: Olasılık fonksiyonlarından diğeri sürekli olasılık fonksiyonu ise örneklem uzayından elde edilen sayılamayacak sonsuz sayıda ve ayrık olmayan sonuçları içermektedir.
Kesikli olasılık fonksiyonu ile sürekli olasılık fonksiyonu arasındaki temel farkı şöyle ifade edilebilir: Kesikli olasılık fonksiyonunda kesikli örneklem uzayı noktaları baz alırken, sürekli olasılık fonksiyonunda sürekli örneklem uzayı aralıklarla ilgilenmektedir.
Bahsedilen kesikli ve sürekli olasılık fonksiyonlarına göre dağılımlar iki ana başlık altında verilmektedir.
A) Kesikli Dağılımlar (Discrete Distributions)
- Bernoulli Dağılımı
- Kesikli Uniform Dağılımı
- Binom Dağılımı
- Poisson Dağılımı
- Negatif Binom Dağılımı
- Geometrik Dağılım
- Hipergeometrik Dağılımı
B) Sürekli Dağılımlar (Continuous Distributions)
- Normal Dağılım
- Tekbiçimli Uniform Dağılım
- Cauchy Dağılımı
- t Dağılımı
- F Dağılımı
- Ki-kare Dağılımı
- Üstel Dağılım
- Weibull Dağılımı
- Lognormal Dağılımı
- Birnbaum-Saunders
- Gamma Dağılımı
- Çift Üstel Dağılımı
- Güç Normal Dağılımı
- Güç Lognormal Dağılımı
- Tukey-Lambda Dağılımı
- Uç Değer Tip I Dağılımı
- Beta Dağılımı
Bernoulli Dağılımı
Olasılık teorisinde adını İsviçreli matematikçi Jacob Bernoulli’den alan Bernoulli dağılımı, bir denemenin iki sonucu (başarılı- başarısız, evet-hayır) olması durumunda kullanılan kesikli bir olasılık dağılımıdır.
Bernoulli dağılımında deney bir kez yapılarak başarılı olma durumu ile ilgilenilir. Eğer deney birden fazla ve bağımsız olarak tekrarlanılıp ve başarılı olma durumu ile ilgilenilirse o zaman Bernoulli dağılımının özel bir durumu olan Binom dağılımının kullanılması gerekmektedir. Bernolli dağılımının hesaplanmasında kullanılan parametreler Tablo 1’de verilmiştir.
Tablo 1: Bernoulli Dağılımı Parametreleri

Bernoulli Olasılık Kitle Fonksiyonu (PMF)
Tablo 1’deki parametreler kullanılarak oluşturulan Bernoulli olasılık kitle fonksiyonu (pmf) aşağıdaki eşitlikte verilmiştir.
f(x) = px(1 − p)1−x
Örnek Uygulamalar
Örnek uygulamalara geçilmeden önce R’da yüklenmesi gereken kütüphaneleri aşağıda verelim. Daha önce aşağıdaki kütüphaneler kurulmamışsa lütfen kurunuz. R studio’yu sıklıkla kullandığım için gerek arayüzünün kullanım kolaylığı gerekse verimli olması açısından R konsol yerine R Studio arayüzünün kullanılması önerilmektedir. Eğer R yüklü değilse yapılan bu işlemleri bulutta yer alan R programlama yazılımını da kullanarak yapabilir ve R Studio arayüzünden bu platform üzerinden yararlanabilirsiniz. Sıklıkla bulut üzerindeki R Studio’yu da şahsen kullanmaktayım. Aşağıda linkten buluta giriş sağlayabilirsiniz. Sıklıkla
RStudio Cloud: https://login.rstudio.cloud/
gereklikütüphaneler<-sapply(c("dplyr","tibble","tidyr","ggplot2","formattable","ggthemes","readr","readxl","xlsx","ggpubr","formattable", "ggstance"), require, character.only = TRUE)
gereklikütüphaneler
Örnek 1: Ortalama, Varyans, Basıklık ve Çarpıklık Değerlerinin Hesaplanması
İlk olarak Bernoulli dağılımında başarı olasılığı verilen bir deneyin ortalama, varyans, basıklık ve çarpıklık değerlerine bakalım. Başarı olasılığımız (p) 0,4 olsun. Örnek uzayımız her koşulda iki çıktı olan {0,1}’dir. Aşağıda yazılan R kod bloğunda istenen parametre değerlerini hesaplayalım.
x<-0:1#örneklem uzayı
p<-0.4#başarı olasılığı
ortalama=p
varyans=p*(1-p)
carpiklik=(1-2*p)/sqrt(varyans)
basiklik= (1/varyans)-6
formattable(cbind(ortalama, varyans,carpiklik, basiklik) %>% as_tibble() %>% mutate_if(is.numeric, round,3))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra Bernoulli dağılımına ait elde edilen ortalama, varyans, çarpıklık ve basıklık değerleri aşağıdaki tabloda verilmiştir.

Örnek 2: Kitle Olasılık Fonksiyonu (PMF)’nun Hesaplanması
Türkiye haritasında tesaüfi çekilen bir ilin büyükşehir olup olmama durumu ile ilgileniliyor. Büyükşehir seçilmesi başarı olarak ifade edildiği durumdaki kitle olasılık fonksiyonunu oluşturarak, hem olasılığı hesaplayalım hem de grafik üzerinde gösterimini yapalım.
Bilinenler:
Örneklem uzayı (x) ={Büyükşehir gelmemesi (0), Büyükşehir gelmesi (1)}
İl sayısı = 81
Büyükşehir sayısı = 30
Büyükşehir seçilme olasılığı (p) = 30/81 = 0,370
Şimdi verilenleri aşağıda yazdığım R kod bloğunda yerine koyalım.
x<-0:1# Örneklem uzayı (x) ={Büyükşehir gelmemesi (0), Büyükşehir gelmesi (1)}
p<-30/81# büyükşehir gelme olasılığı
names(x)<-c("Büyükşehir Gelmemesi", "Büyükşehir Gelmesi")
okf <- p^x * (1-p)^(1-x) #oks: olasılık kitle fonksiyonu (pmf)
okf
#grafiğini çizmek için
barplot(okf, col="orange", ylim=c(0,max(okf)), main="Bernoulli Olasılık Kitle Fonksiyonu")
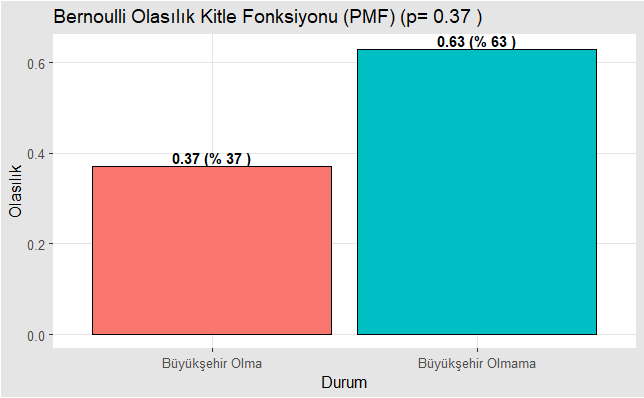
Yukarıdaki R kod bloğu çalıştırıldıktan sonra elde edilen olasılık değerleri Büyükşehir gelme ve gelmeme durumuna göre aşağıda verilmiştir. Elde edilen bulgular 81 il içerisinden Büyükşehir gelmesi durumunun olasılığının 0,37 (% 37) olduğunu göstermektedir.
Büyükşehir Gelmemesi Büyükşehir Gelmesi
0.6296296 0.3703704
Olasılık değerlerine elde ettikten sonra R kod bloğundaki ilgili kısmı çalıştırarak olasılık dağılımının grafiğini aşağıda verelim.

Bu sonuçların hepsini bir arada verecek aşağıda oluşturduğum fonksiyon ile de yapılması mümkündür. Oluşturduğum bu fonksiyonla ayrıca dağılımın varyansı, ortalaması, çarpıklık ve basıklık değerleri de elde edilebilmektedir.
# Olasılık kitle fonksiyonunu oluşturmak.
okff <- function(Vaka_Sayisi, Basarili_Vaka_Sayisi) {
p<-Basarili_Vaka_Sayisi/Vaka_Sayisi
sonuc <- tibble(Olasilik=matrix(round(p^c(0,1)* (1-p)^(1-c(0,1)),4), byrow=F, ncol=1)) %>% add_column(Durum=as.factor(c("Büyükşehir Olmama", "Büyükşehir Olma")), .before="Olasilik")
print(sonuc)
ortalama<-p
varyans<-p*(1-p)
carpiklik<-(1-2*p)/sqrt(varyans)
basiklik <-(1/varyans)-6
print(formattable(cbind(ortalama, varyans,carpiklik, basiklik) %>% as_tibble() %>% mutate_if(is.numeric, round,3)))
grafik<-sonuc %>% ggplot(aes(x=Durum, y=Olasilik, fill=Durum)) +
geom_bar(colour="black", stat="identity") +
guides(fill=FALSE) +
ggtitle(paste("Bernoulli Olasılık Kitle Fonksiyonu (PMF)","(p=",round(p,2),")")) +
ylab("Olasılık")+
theme_igray() +
geom_text(aes(label=paste(round(Olasilik,3),"(%",round(Olasilik*100,1),")")), position=position_dodge(width=0.9), vjust=-0.25, colour = "black", fontface = "bold")
print(grafik)
}
# Fonksiyonu çağırmak için: aşağıdaki alanı problem çözümünde kullanabilirsiniz.Sadece değerleri değiştirmeniz yeterli olacaktır.
okff(Vaka_Sayisi=81, Basarili_Vaka_Sayisi=30)
Yukarıdaki R kod bloğunda programlama mantığıyla geliştirdiğim fonksiyonun çalıştırılmasından sonra ilk olarak olasılıkları aşağıda verelim.

Olasılıkları verdikten sonra Bernoulli dağılımına ait tanımlayıcı istatistikleri verelim.

Şimdi de olasılıklara ilişkin grafiğimizi verelim.
Bernoulli Kümülatif Dağılım Fonksiyonu (CDF)
Bernoulli olasılık dağılımda kümülatif dağılım fonksiyonu aşağıdaki eşitlik yardımıyla hesaplanmaktadır.
FX(x;p)=(1−p)1−x
Örnek 3: Bernoulli Kümülatif Dağılım Fonksiyonunun Hesaplanması
Aşağıda yazılan R kod bloğunda ise yukarıdaki Büyükşehir örneğinden hareketle kümülatif dağılım fonksiyonu hesaplanmıştır.
x<-0:1
p<-30/81#Büyükşehir olma olasılığı
q<-1-p# (1-p)#Büyükşehir olmama olasılığı
(1-p)^(1-x)#Kümülatif dağılım fonksiyonu
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen toplam olasılık değeri ile Büyükşehir olmama olasılığı aşağıda verilmiştir. Büyükşehir olma olasılığı aşağıdaki toplam olasılık değeri ile Büyükşehir olmama olasılığı arasındaki farka eşittir.
[1] 0.6296296 1.0000000
Bernoulli Dağılımından Örneklem Seçimi
Bernoulli dağılımına uygun olarak yukarıdaki Büyükşehir örneğinden hareketle tekrarlı basit tesadüfi örneklem yöntemini kullanarak sonuçları Büyükşehir olma (1), Büyükşehir olmama durumu olan 1000 örneklemi olasılıkları dikkate alarak üretelim.
x<-c("Büyüksehir Olma", "Büyükşehir Olmama")
#x<-0:1
p<-30/81#Büyükşehir olma olasılığı
q<-1-p# (1-p)#Büyükşehir olmama olasılığı
n<-sample(x, size =1000, replace=T, prob=c(p, q))#tekrarli basit tesadüfi örnekleme yöntemi kullanılarak olasılık değerlerine göre 1000 örneklem üretilmiştir.
grafikorneklem<-as_tibble(n) %>% mutate_if(is.character, as.factor) %>% group_by(value)%>% summarise(n=n())%>% rename(Durum=value) %>% ggplot(aes(x=Durum, y=n, fill=Durum)) + geom_bar(stat="identity") + ggtitle(paste("Bernoulli Olasılık Dağılımı Örneklem","(p=0,37)")) + ylab("Sıklık")+ geom_text(aes(label=paste("n=",n)), position=position_dodge(width=0.9), vjust=-0.25, colour = "black",fontface = "bold")+ theme_cleveland()
grafikorneklem
Yukarıdaki R kod bloğunun çalıştırılmasından Bernoulli dağılımına uygun olarak üretilen örnekleme ilişkin grafik aşağıda verilmiştir.
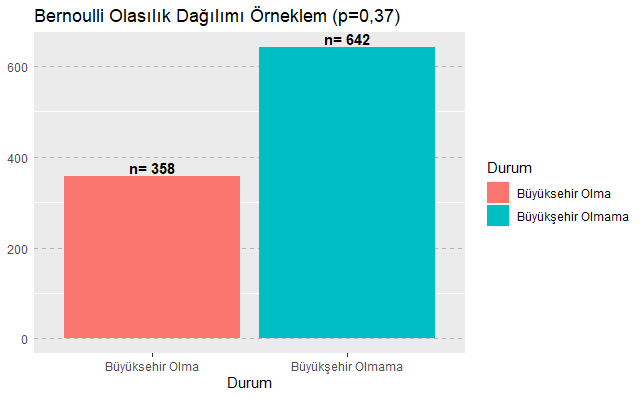
Yapılan bu çalışma ile özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına bir katkı sunulması amaçlanmıştır.
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
- http://people.stern.nyu.edu/adamodar/New_Home_Page/StatFile/statdistns.htm
- https://statisticsglobe.com/bernoulli-distribution-in-r-dbern-pbern-qbern-rbern
- https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Distributions.html
- https://my.ilstu.edu/~wjschne/442/SimulatingRandomData.html#bernoulli-distribution
- https://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm
- RStudio Cloud: https://login.rstudio.cloud/
- Matematiksel İstatistik, İsmail Erdem, Gözden Geçirilmiş ve Genişletilmiş 3. Baskı.
- The R Project for Statistical Computing. https://www.r-project.org/