Z Tablosuna Göre Güven Aralığının Hesaplanmasına Yönelik Bir Simülasyon Çalışması: A Simulation Study for Calculating Confidence Interval by Z Table

Güven aralıkları ingilizce ifadeyle confidence interval (CI) hem sahadan veri toplama yöntemleriyle elde edilen birincil verilerin hem de veri tabanlarından elde edilen işlenmiş ikincil verilerin analizinde çok yoğun bir şekilde kullanılmaktadır. Peki nedir bu güven aralığı? Güven aralığının hesaplanması için hangi parametrelere ihtiyaç vardır? Güven aralığı nasıl hesaplanır? Güven aralığını etkileyen faktörler nelerdir? Tanımlayıcı ve çıkarımsal istatistiklerin rolü nedir? Hipotez testlerinde yapılan hatalar nelerdir? Bu çalışmada bahsedilen bu sorulara cevaplar bulunacaktır. Bu amaçla olasılıklı örneklem yöntemlerinden biri olan ön yargısız (without bias) basit tesadüfi tekrarsız örneklem yöntemi kullanılmıştır. Basit tekrarlı örneklem yöntemi ile ise rastgele beden kitle endeksi verileri üretilmiştir. Üretilen bu sentetik veriler üzerinden deneysel güven aralığı çalışması hazırlanmıştır. Diğer programlama dilleri kullanılarak veya paket programlar üzerinde de bu çalışmanın yapılması her zaman mümkündür. Bunu da yapabilirdim ancak Microsoft Office Excel 2016 kullanılarak güven aralığı çalışması yapılmasının daha uygun olacağını düşündüm. Bunun nedeni excel üzerinde okuyucuya fonksiyon (formül) etkileşimleri gösterilerek konu hakkında daha fazla katkı sunulması amaçlanmasıdır. İki farklı güven aralığı çalışmasına yer verilmiştir. İlkinde güven aralığı çalışmasında elde edilen değerler sabitlenmiştir. İkincisi ise simülasyona izin verecek dinamik bir şekilde excel uzantılı dosya içerisinde sunulmuştur.Bunun nedeni seçilen örneklemlerdeki parametre ve güven aralıkları değişimlerinin karşılaştırmalı ve dinamik olarak sunulmak istenmesidir.

Tanımlayıcı istatistiklerin rolü nedir?

Adından da anlaşılacağı gibi, tanımlayıcı istatistikler (descriptive statistics) bir veri kümesini tanımlar. Burada, bir araştırmacının bir veri seti hakkında bilmek isteyebileceği üç şeyi nasıl belirleyeceğimizi tartışıyoruz:

1. Merkezi eğilim noktaları,
2. Değişkenlik miktarı (varyans derecesi)
3. İki veya daha fazla değişkenin birbiriyle ilişkilendirilme derecesi.

Merkezi Eğilim Ölçüleri

Merkezi bir eğilim noktası, verilerin etrafında döndüğü bir noktadır, belirli bir değişkenle ilgili verilerin etrafında dolaştığı bir orta sayıdır. İstatistik dilinde, böyle bir noktayı belirleme tekniklerine atıfta bulunmak için merkezi eğilim ölçüleri terimini kullanıyoruz. Merkezi eğilimin yaygın olarak kullanılan üç ölçüsü mod, medyan (ortanca) ve ortalamadır ve her biri kendi özelliklerine ve uygulamalarına sahiptir.

Mod, en sık meydana gelen tek sayı veya puandır. Ortanca, bir puan setinin sayısal merkezidir. Ortalama ise belirli bir değişken için puanların aritmetik ortalamasıdır. Hesaplamak için tüm puanların toplamını hesaplıyoruz (her gerçekleştiğinde her puanı ekliyoruz) ve ardından toplam puan sayısına bölüyoruz.

Ortalama ayrıca istatistiksel analizlerde ve araştırma raporlarında en yaygın olarak kullanılan merkezi eğilim ölçüsüdür. Bununla birlikte, yalnızca aralık veya oran verileri için uygundur, çünkü yalnızca sayılar belirli bir ölçek boyunca eşit aralıkları yansıttığında bir ortalamayı hesaplamak matematiksel olarak mantıklıdır.

Medyan, sıralı verilerde daha uygundur. Medyan, bir araştırmacı bir yönde veya diğerinde oldukça çarpık bir veri kümesiyle uğraşırken de sıklıkla kullanılır. Medyanlar genellikle aile geliri ve finansal varlıkların düzeylerinde merkezi eğilimi yansıtmak için kullanılır; çoğu aile geliri ve hane halkı varlıkları ölçeğin alt ucunda kümelenmiştir ve yalnızca çok azı bu aralıkta yayılmıştır. Buradan medyanın uç değerlerden etkilenmediği anlaşılmaktadır.

Her durumda, temel bir ilke geçerlidir: Verilerin konfigürasyonu, o özel durum için en uygun merkezi eğilim ölçüsünü belirler. Veriler normal dağılım gösteren bir eğriye yaklaşan bir dağılıma yakınsarsa, bir merkezi eğilim ölçüsü gerektirirler. Eğer bir ogive-eğri niteliğine sahiplerse (bir büyüme durumunun özelliği), başka bir ölçüt gerekir. Birden fazla zirveye sahip olan çok modlu bir dağılım, yine de üçüncü bir yaklaşımı gerektirebilir; örneğin, araştırmacı onu iki veya daha fazla mod açısından tanımlayabilir. Araştırmacı, ancak verilerin özelliklerinin dikkatli ve bilinçli bir şekilde değerlendirilmesinden sonra en uygun istatistiği seçebilir.

Bu nedenle, veri analizlerinde istatistik kullanan araştırmacılar için temel bir kuralı vurgulamalıyız: Verilerin doğası istatistiksel tekniği belirler, tersi bir durum geçerli değildir. Tıpkı doktorun belirli hastalıklar ve bozukluklar için hangi ilaçların mevcut olduğunu bilmesi gerektiği gibi, araştırmacının da belirli araştırma taleplerine hangi istatistiksel tekniklerin uygun olduğunu bilmesi gerekir. Tablo A, her bir ölçünün uygun olduğu çeşitli veri türleri ile birlikte merkezi eğilim ölçüleri ve kullanımlarının bir özetini sunmaktadır.

Tablo A: Farklı Veri Türleri İçin Merkezi Eğilim Ölçülerini Kullanma

Merkezi Eğilim Ölçüsü	Nasıl Belirlenir (N = puan sayısı)	Uygun Olduğu Veriler
Mod	En sık meydana gelen puan belirlenir.	● Nominal, sıra, aralık ve oran ölçek türündeki veriler ● Çok modlu dağılımlar (bir dağıtımın birden fazla zirvesi olduğunda iki veya daha fazla mod tanımlanabilir)
Medyan	Puanlar en küçükten en büyüğe sıralanır ve orta puan (N tek sayı olduğunda) veya iki orta puan arasındaki orta nokta (N çift sayı olduğunda) belirlenir.	● Sıra, aralık ve oran ölçekleriyle ilgili veriler ● Oldukça çarpık veriler
Aritmetik ortalama	Tüm puanlar toplanır ve toplamları toplam puan sayısına (N) bölünür.	● Aralık ve oran ölçekleriyle ilgili veriler ● Normal dağılım gösteren veriler
Geometrik Ortalama	Tüm puanlar birlikte çarpılır ve çarpımlarının N’inci kökü hesaplanır.	● Oran ölçekleriyle ilgili veriler ● Bir büyüme (ogive) eğrisine yakın olan veriler (Örneğin, büyüme verileri)

Kaynak: Leedy ve Ormrod (2021). Practical Research: Planning and Design

Değişkenlik Ölçüleri: Dağılım ve Sapma

Veri merkezi eğilim noktası etrafında ne kadar çok kümelenirse, belirli bir veri noktasının nerede olduğuna dair doğru bir tahminde bulunma olasılığı o kadar artar. Şekil A’da gösterildiği gibi, ortalamaya yakın kümelenirlerse veriler daha benzerdir. Onları dağıtın ve tekdüzeliklerinin bir kısmını kaybederler; daha çeşitli, daha heterojen hale gelirler. Belirli veri noktaları ortalamadan uzaklaştıkça, kendilerini “ortalama” yapan kaliteyi giderek daha fazla kaybederler.

Şekil A: Değişkenlikte Farklılaşan Dağılımlar

Kaynak: Leedy ve Ormrod (2021). Practical Research: Planning and Design

Değişkenliğin en basit, en açık göstergesi, verilerin en düşük değerden en yüksek değere yayılmasını gösteren aralıktır:

Aralık = En yüksek puan – En düşük puan.

Aralığın hesaplanması kolay olmasına rağmen, değişkenliğin bir ölçüsü olarak sınırlı kullanışlılığa sahiptir ve aşırı üst veya alt sınırlar serideki diğer değerlerden atipik ise yanıltıcı olabilir.

Diğer değişkenlik ölçüleri, başlangıç noktası olarak daha az uç değerler kullanır. Böyle bir ölçü, çeyrekler arası aralıktır. Dağılımı dört eşit parçaya bölersek, 1. çeyrek grup üyelerinin % 25’inin altında olduğu bir noktada yer alır. 2. Çeyrek, grubu iki eşit parçaya böler ve medyan ile aynıdır. 3. çeyrek, değerlerin % 75’inin altında olduğu bir noktada yer alır. Çeyrekler aralığı, Çeyrek 3 (75. yüzdelik nokta) eksi Çeyrek 1’e (25. yüzdelik nokta) eşittir:

Çeyrekler arası aralık = 3. Çeyrek – 1. Çeyrek

Böylece, çeyrekler arası aralık bize dağılımdaki vakaların % 50’si için aralığı verir. Çeyrekler medyan ile ilişkili olduğundan, merkezi eğilim ölçüsü olarak medyanı kullanan herhangi bir araştırmacı, çeyrek sapmayı da değişkenlik için olası bir istatistiksel ölçü olarak dikkate almalıdır. Sıralı verilerle veya çok çarpık verilerle çalışırken, bazı araştırmacılar, en düşük ve en yüksek sayıların yanı sıra Çeyrek 1, ortanca (aynı zamanda Çeyrek 2’dir) ve Çeyrek 3’ten oluşan beş göstergeyi raporlar.

Şimdi bunun yerine ortalamayı başlangıç noktası olarak kullanalım. Her bir puanın ortalamadan ne kadar uzakta olduğunu belirlediğimizi hayal edin. Yani, her puan ile ortalama arasındaki farkı hesaplıyoruz (bu farka sapma diyoruz). Tüm bu farkları toplarsak (artı ve eksi işaretlerini göz ardı ederek) ve ardından toplamı puan sayısına bölersek (bu, puan ortalaması farklılıklarının sayısını da yansıtır), herhangi bir puan ile ortalama arasındaki farkların ortalamasını alırız. Bu işlem bazen ortalama sapma (AD) olarak adlandırılır. Ortalama sapma eşitliği:

Burada | X – M |, artı ve eksi işaretleri dikkate alınmadan X-M anlamına gelir. Diğer bir deyişle, her bir puan ile ortalama arasındaki farkın mutlak değeridir.

Ortalama sapma kolayca anlaşılır ve bu nedenle bazı anlamlar içerir. Başka bir istatistiksel prosedür düşünülmediğinde kabul edilebilir. Birincil zayıflığı, mutlak değerleri kullanmasıdır. Bunun yerine, hesapladığımız puanda artı ve eksi işaretlerini tutarsak ne olacağını hayal edin. Ortalamanın solunda bulunan (ve dolayısıyla ortalamadan daha küçük bir değere sahip olan) herhangi bir sayı için, sayı ile ortalama (X-M) arasındaki fark negatif bir sayı olacaktır. Buna karşılık, ortalamanın sağında bulunan herhangi bir sayı, pozitif bir X-M değeri verir. Tüm olumlu ve olumsuz sapmaları bir araya getirdiğimizde, birbirlerini tamamen dengeleyecekler, esasen birbirlerini “iptal edecekler” ve genel bir sıfır toplamı vereceklerdi. Ortalama sapma, artıları ve eksileri göz ardı ederek bu sorunu ortadan kaldırır. Yine de bu oldukça şüpheli bir prosedürdür. Sevmediğimiz şeyleri görmezden gelmek ne sağlam matematik ne de sağlam araştırma uygulamasıdır.

Ortalama sapma formülünden farklı olarak, standart sapma formülü, mutlak değerle negatifleri pozitiflere dönüştürür. Daha spesifik olarak formül, puan-ortalama farklılıklarının her birinin karesinin alınmasını gerektirir. Örneğin, (X-M)².

Aritmetikte, negatif bir sayıyı kendisiyle çarptığımızda, sonuç pozitif bir sayıdır. Elbette aynı şey pozitif bir sayının karesini almak için de geçerlidir; dolayısıyla, pozitif farklılıkları dengelemek için negatif puan – ortalama farkı bu durumda yoktur.

Standart bir sapmayı hesaplamak için (sırasıyla bir popülasyon parametresi ve örneklem istatistiği için σ veya s olarak sembolize edilir), ortalama sapmanın hesaplanmasına benzer bir prosedür izliyoruz. Bununla birlikte, puanın mutlak değerlerini elde etmek yerine – ortalama farklar, bu farkların her birinin karesini alırız. Daha sonra tüm farkların toplamını (Σ) hesaplıyoruz, bu toplamı puan sayısına böleriz ve son olarak yeni elde edilen bölümün karekökünü buluruz. Bu nedenle, popülasyon standart sapmanın formülü aşağıdaki gibidir:

Standart sapma, istatistiksel prosedürlerde en yaygın olarak kullanılan değişkenliğin ölçüsüdür. Birçok istatistiksel prosedür, standart sapmaya ek olarak veya bunun yerine ikinci, ilgili bir değişkenlik ölçüsü kullanır. Bu istatistik, basitçe standart sapmanın karesi olan varyans olarak bilinir:

Normal ve normal olmayan dağılımların karakteristikleri nelerdir?

Genel olarak normal dağılım veya normal eğri olarak adlandırılan bu model için çan eğrisi terimini de görebilirsiniz. Normal dağılımın birkaç ayırt edici özelliğe sahiptir:

• Yatay olarak simetriktir. Bir taraf, diğer tarafın aynadaki yansımasıdır, yani eğri simetriktir.
• En yüksek noktası orta noktasıdır. Daha fazla insan (veya araştırmanın odağı olan diğer birimler), eğri boyunca başka herhangi bir noktada olduğundan daha tam ortada yer alır. İstatistiksel terimlerle, merkezi eğilimin yaygın olarak kullanılan üç ölçüsü, mod, medyan ve ortalama (tümü kısaca açıklanacak) bu noktada birbirine eşittir.
• Nüfusun tahmin edilebilir yüzdeleri, eğrinin her iki bölümünde bulunur. Eğriyi standart sapmasına göre bölersek (ayrıca kısaca açıklanacaktır), popülasyonun belirli yüzdelerinin her iki kısmında yer aldığını biliyoruz. Özellikle, popülasyonun yaklaşık % 34,1’i ortalama ile ortalamanın altındaki bir standart sapma arasındadır ve diğer % 34,1’i ortalama ile ortalamanın üzerindeki bir standart sapma arasındadır. Nüfusun yaklaşık % 13,6’sı ortalamanın altında bir ila iki standart sapma arasında yer alırken, diğer % 13,6’sı ortalamanın üzerinde bir ve iki standart sapma arasında yer alır. Kalan % 4,6, dağılımın her bir ucunda % 2,3 ile ortalamadan iki veya daha fazla standart sapma uzaktadır. Bu model Şekil B’de gösterilmektedir. Normal dağılımın herhangi belirli bir bölümünde yer alan nüfus oranları, çoğu giriş istatistik kitabında bulunabilir.

Şekil B: Normal Dağılımın İki Kısmındaki Yüzdeler

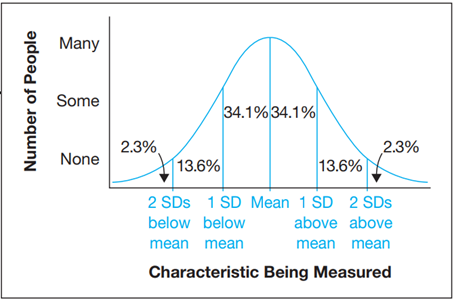
Kaynak: Leedy ve Ormrod (2021). Practical Research: Planning and Design

Ancak bazen veriler normal bir dağılımı yansıtmaz. Örneğin, dağılımları orantısız veya çarpık olabilir. “Çarpıklık”, dağılımın biraz daha bir tarafa uzanan kısmıdır. Tepe orta noktanın solunda yer alıyorsa, dağılım pozitif olarak çarpıktır; tepe orta noktanın sağında yer alıyorsa, dağılım negatif olarak çarpıktır. Ya da belki bir dağılım alışılmadık derecede sivri veya düzdür, öyle ki dağılımın her bir bölümündeki yüzdeler Şekil B’de gösterilenlerden önemli ölçüde farklıdır. Burada, bir leptokürtik dağılımı yansıtan alışılmadık şekilde sivri bir dağılımla ve alışılmadık derecede düzleşen platikürtik bir dağılım olan basıklıktan bahsediyoruz (Bkz. Şekil C).

Şekil C: Normal Dağılımdan Ayrılışlar

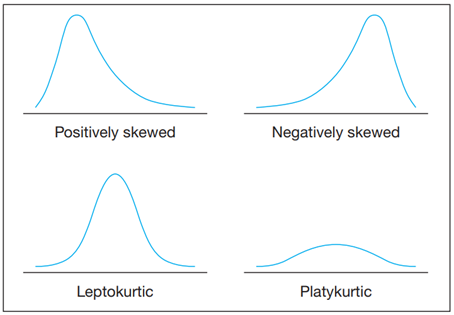
Kaynak: Leedy ve Ormrod (2021). Practical Research: Planning and Design

Parametrik ve parametrik olmayan istatistikler arasında neden seçim yaparız?

İstatistiksel prosedürler seçiminiz, bir dereceye kadar verilerinizin yapısına ve bunların normal dağılımı ne ölçüde yansıttığına bağlı olmalıdır. Parametrik istatistikler olarak bilinen bazı istatistikler, söz konusu popülasyonun doğası hakkında belirli varsayımlara dayanmaktadır. En yaygın varsayımlardan ikisi şunlardır:

• Veriler aralık veya oran ölçeğinde olmalıdır.
• Veriler normal bir dağılım göstermelidir (örneğin, dağılımın merkezi bir yüksek noktası vardır ve ciddi şekilde çarpık, leptokurtik veya platikurtik değildir).

Bu varsayımlardan herhangi biri ihlal edildiğinde, parametrik istatistiklerden elde edilen sonuçlar hatalı olabilir.

Buna karşılık, parametrik olmayan istatistikler bu tür varsayımlara dayalı değildir. Örneğin, bazı parametrik olmayan istatistikler, doğası gereği aralıktan ziyade sıralı olan veriler için uygundur. Diğerleri, bir popülasyon bir yönde veya diğerinde oldukça çarpık olduğunda yararlı olabilir.

“Veriler hakkında herhangi bir varsayımda bulunmaktan (ve muhtemelen ihlal etmekten) kaçınmak için neden her zaman parametrik olmayan istatistikleri kullanmıyorsunuz?” diye düşünüyor olabilirsiniz. Nedeni basit: En karmaşık ve güçlü çıkarımsal istatistiklerimiz parametrik istatistiklere dayanmaktadır. Parametrik olmayan istatistikler, genel olarak, yalnızca nispeten daha basit analizler için uygundur.

İyimser bir not olarak, bazı istatistiksel prosedürlerin belirli varsayımlar açısından sağlam (robust) olduğunu belirtmeliyiz. Yani, bir varsayım karşılanmadığında bile genellikle geçerli sonuçlar verirler. Örneğin, belirli bir prosedür normal dağılımda olduğu gibi leptokürtik veya platikürtik dağılım için de geçerli olabilir, yani aralık verilerinden ziyade sıralı verilerle bile geçerli olabilir.

Çıkarımsal istatistiklerin rolü nedir?

Çıkarımsal (inferential) istatistikler, nispeten küçük örneklemlerden büyük popülasyonlar hakkında çıkarımlar yapmamızı sağlar. Daha spesifik olarak, çıkarımsal istatistiklerin iki ana işlevi vardır:

1. Rastgele bir örneklemden bir popülasyon parametresini tahmin etmek,
2. İstatistiksel temelli hipotezleri test etmek

Özellikle nicel araştırma yaptığımızda çoğu kez, örneklemin alındığı daha büyük popülasyon hakkında bilgi edinmek için bir örneklem kullanıyoruz. Tipik olarak, çalıştığımız örneklem için çeşitli istatistikleri hesaplıyoruz. Çıkarımsal istatistikler bize bu örneklem istatistiklerin genel popülasyonun parametrelerine ne kadar yakın olduğunu söyleyebilir. Örneğin, genellikle merkezi eğilim (örneğin, ortalama veya μ), değişkenlik (örneğin, standart sapma veya σ) ve oran (P) ile ilgili popülasyon parametrelerini tahmin etmek isteriz. Popülasyondaki bu değerler, örneklemdeki M veya X, s ve p parametreleri ile karşılaştırılır.

Buradaki sorun, örneklem istatistikleri temelinde popülasyon yani evren parametrelerini belirlemektir. Popülasyon parametrelerinin istatistiksel tahminleri, örneklemin tesadüfi seçildiği (mutlaka olasılıklı örnekleme yöntemi olmalı) ve toplam popülasyonu temsil ettiği varsayımına dayanmaktadır. Yalnızca tesadüfi, temsili bir örneklem olduğunda, istatistiklerimizin popülasyon parametrelerini ne kadar yakından tahmin ettiğine dair makul tahminlerde bulunabiliriz. Bir örneklem rastgele olmadığı ve dolayısıyla temsili olmadığı ölçüde – seçimi bir şekilde önyargılı olduğu ölçüde – hesapladığımız istatistikler, örneklemin alındığı popülasyonu yansıtmaz.

Popülasyonlardan gelen tesadüfi örneklemler – lütfen burada tesadüfi kelimesine dikkat edin – seçildikleri popülasyonlarla kabaca aynı özellikleri gösterir. Bu nedenle, örneklemimizin ortalama yüksekliğinin, genel popülasyonun ortalamasıyla yaklaşık olarak aynı olmasını beklemeliyiz. Ancak tam olarak aynı olmayacaktır.

Farklı örneklemler – her biri aynı popülasyondan rastgele seçilse bile – neredeyse kesinlikle o popülasyon hakkında biraz farklı tahminler verecektir. Popülasyon ortalaması ile örneklem ortalaması arasındaki fark, tahminimizde bir hata oluşturur. Popülasyonun tam olarak ne anlama geldiğini bilmediğimiz için tahminimizde ne kadar hata olduğunu da bilmiyoruz. Ancak üç şey biliyoruz:

1. Sonsuz sayıda rastgele örneklemlerden elde edebileceğimiz ortalamalar normal bir dağılım oluşturur.
2. Örneklemlerin ortalamalarının ortalaması, örneklemlerin alındığı popülasyonun ortalamasına eşittir (μ). Başka bir deyişle, popülasyon ortalaması, tüm örneklem ortalamalarının ortalamasına eşittir.
3. Örneklem ortalamalarının dağılımının standart sapması, genel popülasyon için ölçülen değişkenin – tüm ortalamalarını hesapladığımız değişken – standart sapmasıyla doğrudan ilgilidir.

Nokta tahminleri mi yoksa aralık tahminleri mi?

Popülasyon parametrelerini tahmin etmek için örneklem istatistikleri kullanırken, iki tür tahmin yapabiliriz: nokta tahminleri ve aralık tahminleri.

Nokta tahmini, popülasyon parametresinin makul bir tahmini olarak kullanılan tek bir istatistiktir; örneğin, popülasyon ortalamasına yakın bir yaklaşım olarak örneklem ortalamasını kullanabiliriz. Nokta tahminlerinin kesin olma gibi görünen faydası olsa da, aslında bu kesinlik yanıltıcıdır. Bir nokta tahmini tipik olarak popülasyondaki eşdeğeriyle tam olarak uyuşmaz.

Daha doğru bir yaklaşım – yine de % 100 güvenilir olmasa da – parametrelerin aralık tahminlerini belirlemektir. Özellikle, bir popülasyon parametresinin muhtemelen içinde bulunduğu bir aralığı belirleriz ve gerçekte orada olma olasılığını belirtiriz. Bu tür bir aralığa genellikle güven aralığı denir, çünkü tahmine belirli bir olasılık seviyesi ekler. Yani, güven aralığı, tahmin edilen aralığın popülasyon parametresini içerdiğine dair belirli bir güven seviyesidir.

Hipotez testlerindeki hatalar nelerdir?

Elbette, belirli bir sonucun tek başına tesadüflerin sonucu olmadığına karar verdiğimizde hata yapmamız mümkündür. Aslında, herhangi bir sonuç muhtemelen tesadüflere bağlı olabilir; Örneğimiz, rastgele seçilmesine rağmen, sadece çekilişin şansı aracılığıyla atipik özellikleri gösteren bir şans olabilir. Aslında bir sonucun şans eseri olduğu halde bir sonucun şans eseri olmadığı sonucuna varırsak, yani eğer boş hipotezi yanlış bir şekilde reddedersek Tip I hatası yapıyoruz (alfa hatası da denir).

Başka bir durumda ise bir sonucun aslında tesadüflerden kaynaklandığı sonucuna varabiliriz. Böyle bir durum, aslında yanlış olan boş bir hipotezi reddetmeyi başaramadığımız durumdur. Bu durum, beta hatası olarak da bilinen Tip II hatasıdır. Örneğin, yeni bir ilacın, insanların kanındaki düşük yoğunluklu lipoprotein kolesterolü (“kötü” kolesterol türü) azaltmadaki etkilerine karşı plasebonun göreli etkilerini test ettiğimizi hayal edin. Belki de yeni ilacı alan kişilerin ortalama olarak, plasebo alanlara göre daha düşük bir kolesterol seviyesine sahip olduğunu görürüz, ancak fark küçüktür. Sadece şansa bağlı olarak 100 üzerinden 25 kez böyle bir farkın ortaya çıkabileceğini keşfederiz ve bu nedenle boş hipotezi muhafaza ederiz. Gerçekte, ilaç, kolesterolü bir plasebodan daha fazla düşürüyorsa, Tip II hatası yapmış oluruz.

İstatistiksel hipotez testi tamamen bir olasılık meselesidir ve her zaman Tip I veya Tip II hata yapma şansımız vardır. Önem düzeyimizi, örneğin 0,05’ten 0,01’e veya belki daha da düşük bir düzeye düşürerek Tip I hata yapma olasılığını azaltabiliriz. Bununla birlikte, bunu yapma sürecinde, Tip II hata yapma olasılığımızı artırıyoruz – aslında yanlış olan boş bir hipotezi reddetmekte başarısız olacağız. Tip II hata olasılığını azaltmak için, anlamlılık düzeyimizi (α) artırmamız gerekir; bu, sıfır hipotezini reddetme olasılığını artırdığı için, aynı zamanda Tip I hata olasılığını da artırır. Açıkçası, o zaman Tip I ve Tip II hataları arasında bir denge vardır: Birini yapma riskini her azalttığınızda, diğerini yapma riskini artırırsınız.

Yeni bir araştırmacı için önemsiz sonuçlar elde etmek son derece sinir bozucu olabilir – istatistiksel bir bakış açısıyla, sadece tesadüflere bağlı olanlar. Aşağıda, Tip II hata yapma olasılığını azaltmak ve böylece yanlış bir sıfır hipotezini doğru bir şekilde reddetme olasılığını artırmak için dört öneri bulunmaktadır. Başka bir deyişle, bunlar istatistiksel bir testin gücünü artırmak için önerilerdir:

• Mümkün olduğu kadar büyük bir örneklem kullanın. Örneklem ne kadar büyükse, hesapladığınız istatistikler gerçek popülasyon parametrelerinden o kadar az farklılık gösterir.
• Değerlendirme araçlarınızın geçerliliğini ve güvenilirliğini en üst düzeye çıkarın. Bir araştırma çalışmasındaki değerlendirme araçları nadiren mükemmel (% 100) geçerliliğe ve güvenilirliğe sahiptir, ancak bazı araçlar diğerlerinden daha geçerli ve güvenilirdir. Yüksek geçerlilik ve güvenilirliğe sahip araçları veya diğer değerlendirme stratejilerini kullanan araştırma projelerinin istatistiksel olarak anlamlı sonuçlar vermesi daha olasıdır.
• Mantıksal olarak savunulabilir ve lojistik olarak pratikse, bağımlı değişkeninizin tekrarlanan ölçümlerini elde edin. Diğer şeyler eşit ya da sabit olduğunda, her katılımcı için belirli bir davranış veya özelliğin tekrarlanan ölçümleri istatistiksel analizlerin gücünü artırır. Tekrarlanan ölçümler, (a) her bir katılımcı için genel değerlendirme puanlarının güvenilirliğini artırarak ve/veya (b) değerlendirme puanlarındaki olası değişkenlik kaynakları olarak konular arasındaki farklılıkları istatistiksel olarak kontrol ederek istatistiksel gücü artırır.
• Mümkün olduğunca parametrik olmayandan ziyade parametrik istatistikleri kullanın. Genel bir kural olarak, parametrik olmayan istatistiksel prosedürler parametrik tekniklerden daha az güçlüdür. “Daha az güçlü” ile parametrik olmayan istatistiklerin tipik olarak, araştırmacının boş bir hipotezi reddetmesini sağlayan sonuçlar elde etmek için daha büyük örnekler gerektirdiğini kastediyoruz. Verilerin özellikleri parametrik istatistik varsayımlarını karşıladığında bu istatistikleri kullanmanızı tavsiye ederiz.

Güven aralığı nedir?

Maliyetlerin yüksekliği, uzun zaman alması, güncel ve derinlemesine veri elde edilmesi gibi temel öncelikler esas alınarak sıklıkla kişiler ya da kurumlar popülasyonun tamamının yerine bu popülasyonu temsil eden örneklem üzerinde araştırma yapmayı tercih ederler. Ancak seçilen örneklemin popülasyonun tamamını temsil etmesi isteniyorsa yeterli örneklem büyüklüğü (n) belirlenerek mutlaka olasılıklı örneklem yöntemlerinden biri veya birkaçı birlikte kullanılmalıdır. Popülasyonun tamamı yerine bu popülasyondan seçilen örneklem söz konusu olunca örneklem popülasyonu ne kadar temsil ediyor sorusu ortaya çıkmaktadır. Güven aralığı ise aslında tam da bize bunu söylemektedir. Güven aralığı, popülasyon ortalamasının tahmincisi olup, bize örneklem ortalamalarının popülasyon ortalamasından ne kadarlık bir sapma olduğunu göstermektedir. Güven aralığının bir alt limit (lower bound)’i ve üst limit (upper bound)’i vardır. Bu alt ve üst limitlerin olması güven aralığına adını vermektedir. Yani örneklemden elde edilen güven aralıkları popülasyon ortalamasını mutlaka içerecektir. Burada güven aralığındaki alt ve üst limitin yorumlanması önem arz etmektedir. Alt ve üst limitler arasında fark ne kadar az ise, diğer bir deyişle güven aralığı genişliği (CI Width) ne kadar dar ise örneklem ortalaması popülasyon ortalamasına o kadar yakın ve popülasyon ortalamasını o kadar doğru tahmin ediyor demektir. Tersi bir durum, örneklem ortalamasının popülasyon ortalamasından uzaklaşması anlamı taşımaktadır ki, bu durum örneklemin popülasyonu kötü temsili anlamına gelmektedir.

Örneğin bir okulda 70 öğrenciden oluşan tesadüfi bir örneklem seçildi ve seçilen her öğrenciye bir matematik testi uygulandı. Matematik testi puanları için % 95 güven aralığı oluştururken alt limitimiz 56,302 puan, üst limitimiz 84,422 puan olsun. Yani 56,302<popülasyon ortalaması< 84,422 olsun. Bu durumda bizim güven aralığı yorumumuz şöyle olacaktır: Bu okuldaki tüm öğrencilerin popülasyonundaki ortalama matematik puanının 56,302 ile 84,422 arasında olduğuna % 95 eminiz demektir. Tersinden düşünürsek % 5 emin değiliz anlamı da çıkmaktadır. Bu % 5’lik hata, bizim Tip I (alfa hatası olarak da bilinir) hatamızı göstermektedir.

Güven aralığının hesaplanması için hangi parametrelere ihtiyaç vardır?

Genel olarak, güven aralığını hesaplamak için adım adım ele alınması gereken parametreler Şekil 1’de verilmiştir.

Şekil 1: Güven Aralığı Hesaplama Adımları

Şekil 1’de görüleceği üzere ilk olarak popülasyondan çekilen örneklemin ortalaması hesaplanır. Ortalama ise aşağıdaki eşitlik yardımıyla hesaplanmaktadır. Eşitlik örneklem ortalamasının hesaplanmasına yönelik olduğu için “X” parametresi kullanılmıştır. Örneklem ortalaması bütün gözlem değerlerinin toplamının toplam gözlem sayısına bölünmesi ile elde edilir. Eşitlikte küçük “n” örneklem büyüklüğünü ifade etmektedir.

Eğer popülasyon ortalamasını hesaplamış olsaydık eşitlikte n yerine büyük “N” e yer verecektik. Burada N popülasyondaki gözlem sayısını ifade etmektedir. Popülasyon ortalaması (μ) ise bütün gözlem değerlerinin toplamının toplam gözlem sayısı (N)’na bölünmesi ile elde edilmekte olup, aşağıdaki eşitlik yardımıyla hesaplanır.

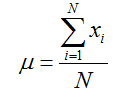
Örnekleme ait standart sapmanın hesaplanmasında ise aşağıdaki eşitlikten faydalanılır. Burada standart sapma ile aslında örneklem ortalamasından ne kadarlık bir sapma olduğunu gösteriyoruz. Adım adım örneklem standart sapması şöyle hesaplanır:

1. Örneklemdeki gözlem değerlerinin ortalaması hesaplanır.
2. Her bir gözlemin gözlem ortalamasından farkı alınır.
3. Her bir gözleme ait hesaplanan farkın karesi hesaplanır.
4. Her bir gözleme ait hesaplanan farkların karesi toplanır.
5. Elde edilen fark kareleri toplamı örneklemdeki gözlem sayısının bir eksiğine bölünür.
6. Elde edilen değerin karesi hesaplanır.

Popülasyon standart sapmasının hesaplanması ise örneklem standart sapmasına benzer olup tek fark karekök içindeki eşitliğin paydasında büyük “N” e, diğer bir deyişle popülasyondaki toplam gözlem sayısına yer verilmesidir. Yukarıda örneklem standart sapmasındaki işlemler popülasyon standart sapması için de yapılır.

Element varyansı ise örneklem standart sapmasının karesi olup, aşağıdaki eşitlik yardımıyla hesaplanmaktadır.

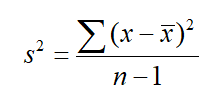
Eğer örneklemin popülasyon içinde yüzdesi (f=(n/N) x 100) %5’ten büyükse örneklem varyansının hesaplanması ve bunun üzerinden standart hata hesaplanması yoluna gidilmelidir. Örneklem varyansı ise aşağıdaki eşitlik yardımıyla hesaplanır.

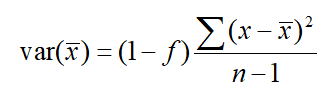
Popülasyon varyansı ise popülasyon standart sapmasının karesinin alınması ile hesaplanır. Aşağıdaki eşitlik yardımıyla popülasyon varyansı hesaplanır.

Standart hata (se), diğer bir ifade ile ortalamanın standart hatası aşağıdaki eşitlik yardımıyla hesaplanmaktadır. Örneklemin standart sapması (s)’nın karekök içerisindeki örneklem gözlem sayısı (n)’na bölünmesi bize ortalamanın standart hatası (standard error of the mean)’nı verir. Standart hatayı aynı zamanda örneklem varyansının karekökünü alarak da hesaplayabiliriz. Örneklem büyüklüğünün artırılması merkezi limit teoremi (central limit teorem)’ne dayalı olarak standart hatayı azaltır ve bu istenen bir durumdur. Böylece, örneklem dağılımı standart normal dağılıma (ortalaması 0, standart sapması 1) evrilir.

Güven aralığı nasıl hesaplanır?

Güven aralığının belirlenmesini sağlayan eşitliklere yer verildikten sonra sırasıyla şimdi çok yalın bir şekilde güven aralığı eşitliğini alt ve üst limitten başlayarak verelim. Bu çalışmada güven aralığı, ortalaması ve standart sapması bilinen bir popülasyon üzerinden hesaplanmıştır.

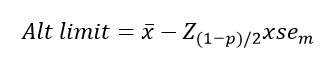
Güven aralığının alt ve üst limitini verdikten sonra bir bütün olarak güven aralığı (confidence interval) eşitliğini verelim. Eşitliğin ortasında yer verilen μ popülasyon ortalamasını göstermektedir. Daha önce de belirtildiği üzere güven aralıklarıyla aslında popülasyon ortalamasını tahmin ediyoruz.

Güven aralığının alt ve üst, diğer bir deyişle iki kuyruklu (two tailed) alfa katsayıları aşağıdaki şekil üzerinde verilmiştir. Z tablosu ortalaması 0, standart sapması 1 olan standart normal dağılımı kullanmaktadır. Standart normal dağılım eğrisi şeklinden dolayı can eğrisi (bell curve) olarak da adlandırılmaktadır. Eğrinin altında alanın toplamı 1’e eşittir. Burada belirlenen güven düzeyi % 95’tir. Bu güven düzeyi s

osyal bilimler dışında özellikle sağlık bilimlerinde % 95’in üzerine çıkabilmektedir daha kesin çıkarımlar (inferences) alınmak istendiğinden.

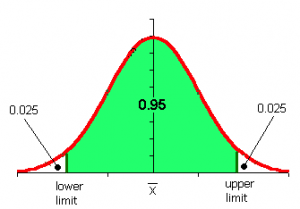
Güven aralığı eşitliğinde görüleceği üzere güven aralığının hesaplanması için gerekli parametreler örneklemin ortalaması, standart hatası (se) ve Z tablo değeridir. Burada Z tablo yerine pekala t tablo değeri de alınabilirdi. Ancak örneklem büyüklüğümüz bu çalışma kapsamında 30’un üzerinde (n>30) olduğu için Z tablosu kullanılmıştır. Ancak isteğe bağlı olarak çalışmada 30’un altında örneklem büyüklüğü (n) belirlenerek t tablo değeri hesaplanabilir. Diğer taraftan, genel olarak sosyal bilimlerdeki istatistiksel analiz ve araştırmalarda güven düzeyleri % 95 olarak alınmaktadır. Ancak bu çalışmada % 90 güven düzeyi benimsenmiştir. Güven düzeyinin % 90 olarak alınması % 10’luk hata payının (alfa hastasının ya da Tip I hatanın) önceden kabul edildiğini göstermektedir. Çalışmanın sonunda paylaştığım simülasyon çalışmasında % 95 üzeri ve altı güven düzeyleri için de güven aralıkları simüle edilebilmektedir.

Sırası gelmişken belirtmekte fayda olduğuna inanıyorum. Güven aralığının kamuoyunda ve literatürde sık sık yanlış yorumlandığı ve adlandırıldığı görülmektedir. Diğer bir deyişle, güven aralığı (confidence interval) ile güven düzeyi (confidence level) karıştırılmaktadır. Burada güven aralığı eğer yüzde olarak ifade edilmişse bu güven düzeyini, yüzde olarak ifade edilmemişse güven aralığını ifade etmektedir. % 95 güven düzeyine sahip olmak, sonuçlarınızın herkese anket yapmış gibi neredeyse aynı olduğundan emin olduğunuz anlamına gelir.

Güven aralığını etkileyen faktörler nelerdir?

Güven aralığını etkileyen faktörler şöyle sıralanabilir:

1. Örneklem büyüklüğü: örneklem büyüklüğü (n) artıkça elde edilen cevapların popülasyonu doğrulama olasılığı o kadar artar. Diğer bir deyişle, örneklem büyüklüğünün artması güven aralığını daraltır. Ancak bu artış lineer olmayabilir.
2. Örneklem seçiminde kullanılan yöntem: eğer örneklem olasıklı örneklem yöntemleri kullanılmadan ya da bu yöntemler kullanılsa bile hatalı örneklem seçimi yapılmışsa güven aralıklarını etkileyebilir. Dolayısıyla popülasyon parametresi olan ortalamalar doğru bir şekilde tahmin edilmemiş olur.
3. Örneklem büyüklüğü sabit tutulduğunda güven düzeyi (% 95’ten % 99’a yükselmesi) yükseldikçe güven aralığı genişler.
4. Örneklem ortalaması arttıkça güven aralığının genişliği aynı kalır. Dolayısıyla, örneklem ortalaması aralığın genişliğinde bir rol oynamaz.
5. Örneklem standart sapmasının azalması varyansın azalması anlamına geldiğinden hata oranı düşer. Bu durum güven aralığının daralmasına ve daha yüksek doğruluk (accuracy) ile popülasyon ortalamasının tahmini anlamına gelmektedir.

Güven aralığından yeterince bahsettikten sonra şimdi uygulama aşamasına geçebiliriz. Uygulamada kullanılan popülasyon veri seti beden kitle endeksi (BKİ) değerlerini içeren ve 1000 (N) gözlemden oluşan sentetik veri setidir. Olasılıklı örneklem yöntemlerinden basit tekrarlı tesadüfi örnekleme yöntemiyle 7 ve 50 aralığında BKİ değerleri üretilmiştir. BKİ değerleri üretilirken Sağlık Bakanlığı resmi web sitesindeki BKİ alt ve üst referans değerlerinden yararlanılmıştır. Burada belirlenen BKİ alt ve üst limitleri şöyledir:

Parametre Değeri	Kategori
18,5 kg/m2’nin altında ise	zayıf
18,5-24,9 kg/m2 arasında ise	normal kilolu
25-29,9 kg/m2 arasında ise	fazla kilolu
30-34,9 kg/m2 arasında ise	I.Derece obez
35-39,9 kg/m2 arasında ise	II.Derece obez
40 kg/m2 üzerinde ise	III.Derece morbid obez

İlk olarak popülasyondan tekrarsız basit tesadüfi örneklem yöntemi kullanarak her birinin örneklem büyüklüğü sırasıyla 456, 758 ve 434 olan 3 farklı örneklem çekilmiştir. Çekilen örneklemleri popülasyondaki ID koduyla birlikte excel (xlsx) formatında aşağıdaki linkten indirebilirsiniz.

Güven aralıklarını vermeden önce popülasyona ait temel parametrelerinin verilmesinin faydalı olduğu düşünülmektedir. Bu amaçla popülasyon parametre değerleri Tablo 1’te sunulmuştur.

Tablo 1: Popülasyon (N) Parametreleri

Popülasyon Parametreleri	Değer
Ortalama (µ)	28,5
Varyans	149,9
Standart Sapma	12,2
N	1000,0

Örneklem gruplarına ait üretilen güven aralıkları ise Tablo 2’de verilmiştir. Tablo 2’ye göre öne çıkan bulgular şöyledir:

• Ortalamasının 28,07 ortalamanın standart hatasının (se) 0,22 olduğu örneklem 2 grubu popülasyon ortalamasını en doğru tahmin eden örnek grubu olarak öne çıkmıştır. Bu grupta güven aralığı genişliği (0,85) diğer gruplara göre daha dar olup güven aralığı (CI) “27,71 ≤ µ ≤28,43” şeklindedir. Buradan örneklem beden kitle endeksi ortalamasının % 90 olasılıkla veya güven aralığında 27,71 ile 28,43 arasında olduğunu söyleyebiliriz. Örneklem 2 grubunu ise güven aralığı genişliği (CI width) 0,71 olan örneklem 2 grubu izlemiştir. Burada güven düzeyi sabit, ancak örneklem büyüklüğü değiştiğinde bu tür bir yargıya vardığımızı özellikle ifade etmek gerekir.

Tablo 2: Örneklem Grubuna Göre Güven Aralıkları

Örneklem Parametreleri	Örneklem 1	Örneklem 2	Örneklem 3
Ortalama (m)	28,61	28,07	28,60
Element Varyans (s^2)	151,16	147,84	150,99
Standart Sapma (s)	12,29	12,16	12,29
Örneklem büyüklüğünün popülasyon içindeki oranı (f)	0,46	0,76	0,43
Finite population correction(fpc) (1-f): Popülasyon düzeltmesi	0,54	0,24	0,57
Örneklem varyansı (var(x))	0,18	0,05	0,20
Standart Hata (se)	0,42	0,22	0,44
Nispi hata (Coefficient of Variation) (CV)	1,48	0,77	1,55
Alfa (a/2) değeri (güven aralığının olasılık değeri)	0,050	0,050	0,050
Z tablo değeri	1,64	1,64	1,64
Güven Aralığı Alt Limit (Lower boundary of CI)	27,91	27,71	27,87
Güven Aralığı Üst Limit (Upper boundary of CI)	29,30	28,43	29,33
Güven Aralığı Genişliği (CI Width)	1,40	0,71	1,46
Güven aralığı gösterimi (CI)	27,91 ≤ µ ≤29,3	27,71 ≤ µ ≤28,43	27,87 ≤ µ ≤29,33

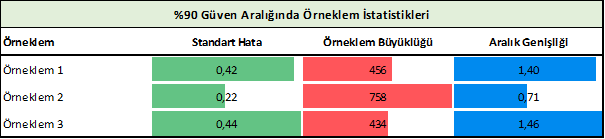
Tablo 2’deki güven aralıkları genişlikleri baz alınarak örneklem gruplarına göre güven aralıkları Tablo 3’te verilmiştir. Görüleceği üzere güven aralığı genişliği en dar olan örneklem grubu 0,71 ile örneklem 1 grubudur. Buradan şöyle bir yorum yapabiliriz: güven düzeyi sabit tutulduğunda örneklem büyüklüğü (n) artıkça standart hata (se) düşer, buna bağlı olarak güven aralığı (CI width) daralır. Eğer biz burada güven düzeyini % 90’dan % 95’e veya % 99’a çıkarmış olsaydık güven aralığı genişleyecekti. Çalışmanın sonunda paylaştığım simülasyonda bunların tamamını test edebilirsiniz.

Tablo 3: Örneklem Gruplarına Göre Güven Aralığı Genişlikleri

Özet Çıkarımlar

1. Güven düzeyi sabit tutulduğunda örneklem büyüklüğü (n) artıkça standart hata (se) azalmakta ve buna bağlı olarak güven aralığı (CI) daralmaktadır.

2. Örneklem büyüklüğü sabit tutulup güven düzeyi artırıldıkça ise güven aralığı genişlemektedir.

3. Örneklem büyüklüğü ve güven düzeyi yükseltildiğinde örneklem büyüklüğüne bağlı olarak güven aralığı daralmakta ve daha kesin sonuçlar alacağımızı göstermektedir. Tabi burada örneklem büyüklüğünün artması tip II hatayı yani beta hastasını azaltırken, diğer taraftan tip 1 hata olarak adlandırılan alfa hatası da azalmaktadır. Ancak genel olarak tip I hata ile tip II hata arasında ters orantı vardır. Yani birini azaltırken diğeri artış göstermektedir. Örneğimizde güven düzeyini 0,90’dan 0,99’a çıkarmamız tip I hatayı azaltmaktadır. Örneklem büyüklüğünü artırmamız ise aynı zamanda testin gücünü de gösteren beta hatasını azaltmaktadır. Ancak bu adımlardan birini artırırken diğeri sabit tutmak ister istemez hatalardan birini azaltırken diğerini de artırmaktadır. Burada önemli olan bir dengenin kurulmasıdır.

Burada Z tablosu üzerinden yapılan güven aralığı deneysel çalışmasının excel uzantılı dosyasını aşağıda linkten indirebilirsiniz.

Z tablosu üzerinden Güven aralığının hesaplanmasına yönelik olarak hazırladığım simülasyonu ise aşağıdaki linkten indirebilirsiniz. Simülasyon çalışmasında bazı sayfalardaki formüller şifre ile korunmuştur. Değişiklik yapılması istenmesi durumundan sayfa korumasının kaldırılması için şifre olarak “tevfik” girilmesi yeterlidir. Özellikle bu simülasyon çalışmasının sahada ve akademide faaliyet gösteren çalışanlara faydalı olacağı düşünülmektedir. Bu çalışmanın içerisinde olasılıklı örneklem seçiminden örneklem büyüklüğünün ve güven düzeylerinin belirlenmesi kadar pek çok konu mevcuttur. Bu simülasyonda örneklem büyüklüğünü sizin belirlemenize gerek bulunmamaktadır.

Faydalı olması ve farkındalık oluşturması dileğiyle.

Bilimle ve teknolojiyle kalınız.

Saygılarımla…

Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.

Note: It can not be cited or copied without referencing.

Yararlanılan Kaynaklar