Bir çok analiz yönteminin temelini olasılık dağılımları oluşturmaktadır. İşin esasında olasılık dağılımları tam anlaşılmadan analiz yöntemleri ile istenilen sonuçların elde edilmesi tek başına bazıları için yeterli olsa da işin felsefesini anlamak açısından kesinlikle yetersizdir. Bu nedenle bu çalışmada öncelikle kesikli (discrete) ve sürekli (continuous) dağılımlar başlıklar halinde verildikten sonra kesikli dağılım türlerinden biri olan Negatif binom dağılımı uygulama örnekleriyle ele alınarak somutlaştırılacaktır. Uygulama örnekleri ağırlıklı olarak R programlama dili kullanılarak adım adım yapılacaktır.
Rastlantı ya da kesin olmayan olaylarla ilgilenen olasılık teorisi, rastlantı olaylarını belirli kurallara göre matematik disiplininde inceleyen bir bilim dalıdır. Burada, rastlantı olayından kasıt gerçekleşmesi şansa bağlı olan önceden bilinmeyen olaylardır.
İstatistikte ve makine öğrenmede, diğer bir deyişle veri biliminde sıklıkla kullanılan örneklem uzayına bağlı olarak olasılık fonksiyon türleri kesikli ve sürekli olmak üzere iki ana başlıkta ele alınmaktadır.
- Kesikli Olasılık Fonksiyonu: Olasılık fonksiyonlarından ilki olan kesikli olasılık fonksiyonu örneklem uzayından elde edilen sonlu veya sayılabilir sonsuz sayıda ayrık sonuçları içermektedir.
- Sürekli Olasılık Fonksiyonu: Olasılık fonksiyonlarından diğeri sürekli olasılık fonksiyonu ise örneklem uzayından elde edilen sayılamayacak sonsuz sayıda ve ayrık olmayan sonuçları içermektedir.
Kesikli olasılık fonksiyonu ile sürekli olasılık fonksiyonu arasındaki temel fark şöyle ifade edilebilir: Kesikli olasılık fonksiyonunda kesikli örneklem uzayı noktaları, sürekli olasılık fonksiyonunda sürekli örneklem uzayı ise aralıkları baz almaktadır.
Bahsedilen kesikli ve sürekli olasılık fonksiyonlarına göre dağılımlar iki ana başlık altında verilmektedir.
A) Kesikli Dağılımlar (Discrete Distributions)
- Bernoulli Dağılımı
- Kesikli Uniform Dağılımı
- Binom Dağılımı
- Poisson Dağılımı
- Negatif Binom Dağılımı
- Geometrik Dağılım
- Hipergeometrik Dağılımı
B) Sürekli Dağılımlar (Continuous Distributions)
- Normal Dağılım
- Tekbiçimli Uniform Dağılım
- Cauchy Dağılımı
- t Dağılımı
- F Dağılımı
- Ki-kare Dağılımı
- Üstel Dağılım
- Weibull Dağılımı
- Lognormal Dağılımı
- Birnbaum-Saunders Dağılımı
- Gamma Dağılımı
- Çift Üstel Dağılımı
- Güç Normal Dağılımı
- Güç Lognormal Dağılımı
- Tukey-Lambda Dağılımı
- Uç Değer Tip I Dağılımı
- Beta Dağılımı
Negatif Binom Dağılımı
Negatif binom dağılımı, bir olayda r’inci başarının x denemede gerçekleşme olasılığını hesaplamada kullanılan kesikli olasılık dağılımlarından biridir. Örneğin, hilesiz bir zarın 7 kez atılması durumunda 6. atışında 4. kez 5 gelme olasılığı bu olasılık dağılımına örnek verilebilir. Bernoulli dağılımı için gerekli varsayımlar bu dağılım için de geçerlidir. Bu dağılım Negative binom regresyon analizinin temelini oluşturmakta olup, bağımlı değişkenin Negatif binom dağılım gösterdiği durumlarda kullanılmaktadır. Negatif binom regresyon analizinde bağımlı değişkenin veri tipi nicel pozitif ve aynı zamanda kesiklidir. Yapılan Covid-19 testlerinin sayısı, doğum sayısı, araba sayısı, vaka sayısı, ölüm sayısı gibi veri tipi nicel ve kesikli olan değişkenler kurulacak Negatif Binom regresyon modellerinde bağımlı değişkene örnek verilebilir.
Negatif Binom dağılımında kullanılan merkezi dağılım ve yayılım ölçüleri aşağıda verilmiştir. Ayrıca örneklem uzayı doğal sayılar kümesi (N)’nden oluşmaktadır. Eşitliklerde bir deneyde istenen sonucun ortaya çıkma olasılığı, diğer bir ifadeyle başarı olasılığı p, istenen sonucun ortaya çıkmama olasılığı ise q=1-p‘dir.
Negatif Binom olasılık dağılımında ortalama;

Negatif Binom olasılık dağılımında varyans;

Teorik olarak Poisson regresyon dağılımında varyansın ve ortalamanın birbirine eşit veya yakın olması istense de uygulamada bu durum pek mümkün olmamaktadır. Genelde pratikte karşılaşılan sorunların başında varyansın ortalamanın üstünde olmasıdır. Bu durum veri setindeki ilgili değişken setindeki gözlemlerin aşırı yayılım (overdispersion) gösterdiği anlamına gelmektedir. Uygulamada az da olsa karşılaşılan diğer durumda ilgili değişken setinin eksik yayılım (underdispersion) göstermesidir. Bu durumda ise varyans ortalamanın çok altındadır. Veri setindeki aşırı ve eksik yayılım durumlarını ortaya koymak için uyum iyiliği testleri (goodness of fit) yaparız. Bu testler analize en uygun yöntemin belirlenmesi için yapılmaktadır. Eğer uyum iyiliği testleri veri setinde aşırı yayılımı gösteriyorsa Poisson regresyon yönteminden vazgeçerek Negatif Binom regresyonu seçeriz. Çünkü Poisson regresyon, diğer bir ifadeyle Poisson dağılım varsayımını ihlal etmişizdir. Benzer şekilde Negatif Binom olasılık dağılımı için de uyum iyiliği testi yaparak dağılımın Negatif Binom dağılımı gösterip göstermediğini test edebiliriz.
Negatif Binom Olasılık Kütle Fonksiyonu (PMF)
Tablo 1’deki parametreler kullanılarak oluşturulan Negatif Binom olasılık kitle fonksiyonu (PMF) aşağıdaki eşitlikte verilmiştir.

x = 0, 1, 2, …, n > 0 ve 0 < p ≤ 1.
Örnek Uygulamalar
Örnek uygulamalara geçilmeden önce R’da yüklenmesi gereken kütüphaneleri aşağıda verelim. Daha önce aşağıdaki kütüphaneler kurulmamışsa lütfen kurunuz. R studio’yu sıklıkla kullandığım için gerek arayüzünün kullanım kolaylığı gerekse verimli olması açısından R konsol yerine R Studio arayüzünün kullanılması önerilmektedir. Eğer R yüklü değilse yapılan bu işlemleri bulutta yer alan R programlama yazılımını da kullanarak yapabilir ve R Studio arayüzünden bu platform üzerinden yararlanabilirsiniz. Sıklıkla bulut üzerindeki R Studio’yu da şahsen kullanmaktayım. Aşağıda linkten buluta giriş sağlayabilirsiniz. Sıklıkla
RStudio Cloud: https://login.rstudio.cloud/
gereklikütüphaneler<-sapply(c("dplyr","tibble","tidyr","ggplot2","formattable","ggthemes","readr","readxl","xlsx","ggpubr","formattable", "ggstance","vcd"), require, character.only = TRUE)
gereklikütüphaneler
Örnek 1: Negatif Binom Dağılımının Test Edimesi
İlk olarak Poisson dağılımında ortalama, varyans, basıklık ve çarpıklık değerlerine bakalım. Aşağıda yazılan R kod bloğunda rnbinom(n, size, prob, mu) fonksiyonu kullanılarak Negatif binom dağılımına uygun popülasyon büyüklüğü (n) 1000 ve ortalama (mu) değeri 5 ve başarılı denemelerin sayısı (size) 20 olan sentetik gözlem değerleri üretelim. Ardından gerçekten 1000 gözlemden oluşan veri setinin Negatif Binom dağılımına uyup uymadığını uyum iyiliği testi ile test edelim. Bu durumda hipotez testlerimiz;
- H0, yani yokluk hipotezimiz veri setinin Negatif Binom dağılımı gösterdiği
- H1, yani alternatif hipotezimiz ise veri setinin Negatif Binom dağılımı göstermediği
şeklinde olacaktır.
#Poisson dağılımına uygun popülasyon büyüklüğü 1000 ve Lambda değeri 1 olan örneklem üretme
set.seed(61)#örneklem uzayının elemanlarını sabitlemek için
nbdorneklem<-rnbinom(n=1000, mu = 5, size = 20)#örneklem uzayı
#Veri setinin histogramı
ggplot(as_tibble(nbdorneklem), aes(x=value))+geom_bar(bins=100,binwidth=.5, fill="red")+
xlab("Örneklem Uzayı")+
ylab("Frekans")+
ggtitle("Veri Setinin Histogramı")+
theme_replace()
#Negatif Binom dağılımı uyum iyiliği testi (goodness of fit)
library(vcd)
veri<-table(nbdorneklem)#sıklıklarını almak için
uyum <- goodfit(veri, type = "nbinomial", method = "MinChisq")
summary(uyum)
plot(uyum, xlab="Örneklem Uzayı", ylab="Frekans", main="Negatif Binom Dağılım Uyum İyiliği Testi Grafiği")
Yukarıdaki R kod bloğunda ilgili alan çalıştırıldığında elde edilen veri setine ait histogram aşağıda verilmiştir. Aşağıdaki histogramda da görüleceği üzere veri seti Negatif Binom dağılımına uygun bir görünüm ortaya koymaktadır.

Yukarıdaki R kod bloğunda ilgili alan çalıştırıldığında elde edilen uyum iyiliği testi (goodness of fit) sonuçları ise aşağıda verilmiştir. Elde edilen sonuçlar istatistiksel olarak anlamlı olmadığı için veri setimiz Negatif Binom dağılımına uygundur (p>0.05). Bu durumda yukarıda belirttiğimiz H0 hipotezimi kabul ediyoruz.
Goodness-of-fit test for nbinomial distribution
X^2 df P(> X^2)
Pearson 0.1449423 1 0.7034163
Şimdi de Negatif Binom dağılımına uygun olarak aynı popülasyon büyüklüğü (N) sahip ancak farklı size (başarılı denemelerin sayısı) ve ortalama (mu) değerleriyle karşılaştırmalı olarak negatif binom dağılıma grafik üzerinde bakalım. Aşağıda yazılan R kod bloğu ile popülasyon büyüklüğü (N) 1000 olan
- mu = 4, size = 10
- mu = 8, size = 20
- mu = 12, size = 30
- mu = 16, size = 40
- mu = 20, size = 50
- mu = 24, size = 60
değerlerine sahip Negatif Binom olasılık dağılım eğrileri çizilmiştir.
set.seed(61)
orneklem<-1000
nby1<-ggdensity(rnbinom(orneklem, mu = 4, size = 10),main="m = 4, s = 10", col="orange", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby2<-ggdensity(rnbinom(orneklem, mu = 8, size = 20),main="m = 8, s = 20",col="orange", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby3<-ggdensity(rnbinom(orneklem, mu = 12, size = 30),main="m = 12, s = 30", col="grey", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby4<-ggdensity(rnbinom(orneklem, mu = 16, size = 40),main="m = 16, s = 40", col="brown", xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby5<-ggdensity(rnbinom(orneklem, mu = 20, size = 50),main="m = 20, s = 50",col="green", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby6<-ggdensity(rnbinom(orneklem, mu = 24, size = 60),main="m = 24, s = 60", col="red", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
ggarrange(nby1,nby2,nby3,nby4,nby5,nby6)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen Negatif Binom dağılım eğrilerine ilişkin grafikler ayrı ayrı aşağıda verilmiştir.
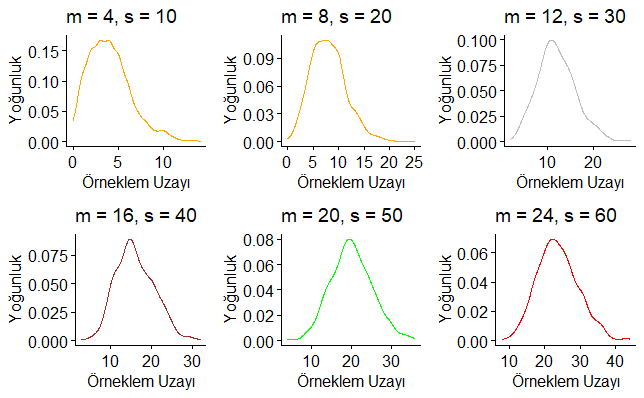
Şimdi de Negatif Binom dağılımına uygun olarak farklı popülasyon büyüklüğüne sahip ancak farklı size ve ortalama (mu) değerleriyle karşılaştırmalı olarak Negatif Binom dağılımlarına grafik üzerinde bakalım. Aşağıda yazılan R kod bloğunda rnbinom(n, size, mu) fonksiyonu ile;
- n=100, mu = 4, size = 10
- n=300, mu = 8, size = 20
- n=500, mu = 12, size = 30
- n=700, mu = 16, size = 40
- n=900, mu = 20, size = 50
- n=1100, mu = 24, size = 60
değerlerine sahip Negatif Binom olasılık dağılım eğrileri çizilmiştir.
set.seed(61)
nby1<-ggdensity(rnbinom(n=100, mu = 4, size = 10),main="N,m,s = 100,4,10", col="orange", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby2<-ggdensity(rnbinom(n=300, mu = 8, size = 20),main="N,m,s = 300,8,20",col="orange", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby3<-ggdensity(rnbinom(n=500, mu = 12, size = 30),main="N,m,s = 500,12,30", col="grey", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby4<-ggdensity(rnbinom(n=700, mu = 16, size = 40),main="N,m,s = 700,16,40", col="brown", xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby5<-ggdensity(rnbinom(n=900, mu = 20, size = 50),main="N,m,s = 900,20,50",col="green", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
nby6<-ggdensity(rnbinom(n=1100, mu = 24, size = 60),main="N,m,s = 1100,24,60", col="red", ,xlab="Örneklem Uzayı",ylab= "Yoğunluk")
ggarrange(nby1,nby2,nby3,nby4,nby5,nby6)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen grafikler aşağıda verilmiştir. Grafik başlıklarında kısaca belirtilen N, popülasyon büyüklüğünü, m ortalama (mu)’yı ve s başarı denemelerin sayısı (size)’nı göstermektedir. Elde edilen bulgular, popülasyon büyüklüğü, ortalama ve başarı denemelerin sayısı (size) artıkça Negatif Binom dağılımının normal dağılıma evrildiğini göstermektedir.

Örnek 2: Kütle Olasılık Fonksiyonu (PMF)’nun Hesaplanması
Negatif Binom kütle olasılık fonksiyon değerlerinin hesaplanmasında daha önce bahsedildiği gibi aşağıdaki eşitlikten faydalanılmıştır.

x = 0, 1, 2, …, n > 0 ve 0 < p ≤ 1. Eşitlikte p başarı olasılığını göstermektedir. Varsayımsal bir örnek vererek konuyu biraz somutlaştıralım.
Covid-19 hastalığına maruz kalan sigara kullanan 65 yaşındaki bireyin bu hastalığa yakalanma olasılığı 0,70 ise bu hastalığa maruz kalan aynı yaşta 20. bireyin bu hastalığa yakalanan 8. birey olma olasılığı nedir?
Burada,
- p=0,70 (hastalığa maruz kalma olasılığı)
- x=20 (hastalığa maruz kalan 20. birey)
- k=8 (hastalığa yakalanan 8. birey)
Yukarıda belirtilen Negatif Binom dağılım eşitliğinde verilenleri aşağıdaki eşitlikte yerine koyarsak,

Yapılan işlemi aşağıdaki R kod bloğunda da verelim kullanılan fonksiyonun görülebilmesi açısından. Aşağıdaki ve yukarıdaki sonuçtan görüleceği üzere aynı yaşta 20. bireyin bu hastalığa yakalanan 8. birey olma olasılığı yaklaşık 0.00154’tür.
options(scipen = 999)#bilimsel notasyondan sayıları kurtarmak için
round(choose(19,7)*(1-0.7)^(20-8)*(0.7)^8,5)#burada choose () fonksiyonu kombinasyon hesaplamasında kullanılmıştır.
#Sonuç:0.00154
Örnek 3: Kütle Olasılık Fonksiyonu (PMF)’nun Hesaplanması
Bu kısımda bir diğer varsayımsal örnekle Negatif Binom dağılımının kütle olasılık fonksiyonunu hesaplayalım.
Bir genel seçimde bir siyasi partinin kazanma olasılığı 0,28’dir. Bu seçimlerden rastgele 8 tanesi alınıp inceleniyor. İncelenen 8. seçimin 6. seçim olma olasılığı nedir?
Bilinenler:
- p=0,28 (seçim kazanma olasılığı)
- x=8 (incelenen 8. seçim)
- k=6 (kazanılan 6. seçim)
Yapılan işlemi aşağıdaki R kod bloğunda da verelim adım adım hesaplama adımlarını görebilmek açısından. Elde edilen sonuca göre incelenen 8. seçimin 6. seçim olma olasılığı yaklaşık 0.00175’tir.
options(scipen = 999)#bilimsel notasyondan sayıları kurtarmak için
round(choose(7,6)*(1-0.28)^(8-6)*(0.28)^6,5)#burada choose () fonksiyonu kombinasyon hesaplamasında kullanılmıştır.
#Sonuç:0.00175
Negatif Binom Kümülatif Dağılım Fonksiyonu (CDF)
Poisson olasılık dağılımda kümülatif dağılım fonksiyonu aşağıdaki eşitlik yardımıyla hesaplanmaktadır. Eşitlikte lp düzeltilmiş beta fonksiyonunu göstermektedir.
Örnek 3: Kümülatif Dağılım Fonksiyonu (CDF)’nunun Hesaplanması
Aşağıda yazılan R kod bloğunda ise varsayımsal olarak kümülatif dağılım fonksiyonu hesaplanmıştır.
options(scipen = 999)
#COVID-19 Ölüm Vakaları
options(scipen = 999)
x<-seq(2, 1000, by = 2)
kdff<-pnbinom(x,size=80, prob=0.6)
kdff#CDF değerleri
sonuc<-kdff %>% as_tibble() %>% mutate_if(is.numeric, round,8) %>% mutate(Orneklem_Uzayı= 1:NROW(kdff), Olasilik=as.numeric(value))
grafik<-sonuc[,-1] %>% ggplot(aes(x=Orneklem_Uzayı,y=Olasilik)) + geom_line(color="red", size=1.5) +
guides(fill=FALSE) +
ggtitle(paste("Negatif Binom Kümülatif DF (CDF)","(","N, p, s=500,0.6, 80", ")")) +
ylab("Olasılık")+
xlab("Örneklem Uzayı")+
theme_igray()+
theme(plot.title = element_text(hjust = 0.5))
grafik
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen kümülatif olasılık (CDF) değerleri aşağıda verilmiştir. Kümülatif olasılık değerlerini hesapladığımız için aşağıda da görüleceği üzere her halükarda son olasılık değeri 1’e eşittir ve böyle olduğu da aşağıda görülmektedir.
[1] 0.0000000000000009852962 0.0000000000000951743775
[3] 0.0000000000038611171739 0.0000000000880213308040
[5] 0.0000000013084356675510 0.0000000138851265693966
[7] 0.0000001118045395017161 0.0000007136876309617969
[9] 0.0000037326667789238904 0.0000164118779021221761
[11] 0.0000619257479359231302 0.0002039325742484081414
[13] 0.0005944565738528822477 0.0015522358262161693818
[15] 0.0036682484040896070829 0.0079160212340880133780
[17] 0.0157226087532808984915 0.0289441668014192715619
[19] 0.0497007147720145148195 0.0800624532242474873378
[21] 0.1216349398293410793981 0.1751403300190932654790
[23] 0.2401127869639744505381 0.3148051925874442713571
[25] 0.3963470874398397625349 0.4811219541307547031828
[27] 0.5652725086793937148144 0.6452155355006015113872
[29] 0.7180583658766382937344 0.7818482658269249041538
[31] 0.8356364747857912833595 0.8793831364239894643475
[33] 0.9137567509547558364247 0.9398891869929757447721
[35] 0.9591386024593491210766 0.9728950784546261942864
[37] 0.9824446049762557420237 0.9888913651254437331417
[39] 0.9931283414023758249201 0.9958420765602931101768
[41] 0.9975375551752201364053 0.9985718004790884450017
[43] 0.9991882994848760857209 0.9995476926711720500052
[45] 0.9997527467041465998321 0.9998673356845434456730
[47] 0.9999300970499609420017 0.9999638103148409395970
[49] 0.9999815823865207953247 0.9999907818172626416953
[51] 0.9999954603979571698957 0.9999977994007636095120
[53] 0.9999989494945618062616 0.9999995059547135412004
[55] 0.9999997710097774383797 0.9999998953562353465330
[57] 0.9999999528355646427613 0.9999999790263622845288
[59] 0.9999999907946935939762 0.9999999960111253249906
[61] 0.9999999982929450581537 0.9999999992782911961697
[63] 0.9999999996984760830543 0.9999999998754768304465
[65] 0.9999999999491528956952 0.9999999999794654259588
[67] 0.9999999999917961179818 0.9999999999967568165005
[69] 0.9999999999987310150829 0.9999999999995085042670
[71] 0.9999999999998114841304 0.9999999999999283906149
[73] 0.9999999999999730215805 0.9999999999999898969705
[75] 0.9999999999999963362640 0.9999999999999986677324
[77] 0.9999999999999995559108 0.9999999999999997779554
[79] 0.9999999999999998889777 1.0000000000000000000000
[81] 1.0000000000000000000000 1.0000000000000000000000
[83] 1.0000000000000000000000 1.0000000000000000000000
[85] 1.0000000000000000000000 1.0000000000000000000000
[87] 1.0000000000000000000000 1.0000000000000000000000
[89] 1.0000000000000000000000 1.0000000000000000000000
[91] 1.0000000000000000000000 1.0000000000000000000000
[93] 1.0000000000000000000000 1.0000000000000000000000
[95] 1.0000000000000000000000 1.0000000000000000000000
[97] 1.0000000000000000000000 1.0000000000000000000000
[99] 1.0000000000000000000000 1.0000000000000000000000
[101] 1.0000000000000000000000 1.0000000000000000000000
[103] 1.0000000000000000000000 1.0000000000000000000000
[105] 1.0000000000000000000000 1.0000000000000000000000
[107] 1.0000000000000000000000 1.0000000000000000000000
[109] 1.0000000000000000000000 1.0000000000000000000000
[111] 1.0000000000000000000000 1.0000000000000000000000
[113] 1.0000000000000000000000 1.0000000000000000000000
[115] 1.0000000000000000000000 1.0000000000000000000000
[117] 1.0000000000000000000000 1.0000000000000000000000
[119] 1.0000000000000000000000 1.0000000000000000000000
[121] 1.0000000000000000000000 1.0000000000000000000000
[123] 1.0000000000000000000000 1.0000000000000000000000
[125] 1.0000000000000000000000 1.0000000000000000000000
[127] 1.0000000000000000000000 1.0000000000000000000000
[129] 1.0000000000000000000000 1.0000000000000000000000
[131] 1.0000000000000000000000 1.0000000000000000000000
[133] 1.0000000000000000000000 1.0000000000000000000000
[135] 1.0000000000000000000000 1.0000000000000000000000
[137] 1.0000000000000000000000 1.0000000000000000000000
[139] 1.0000000000000000000000 1.0000000000000000000000
[141] 1.0000000000000000000000 1.0000000000000000000000
[143] 1.0000000000000000000000 1.0000000000000000000000
[145] 1.0000000000000000000000 1.0000000000000000000000
[147] 1.0000000000000000000000 1.0000000000000000000000
[149] 1.0000000000000000000000 1.0000000000000000000000
[151] 1.0000000000000000000000 1.0000000000000000000000
[153] 1.0000000000000000000000 1.0000000000000000000000
[155] 1.0000000000000000000000 1.0000000000000000000000
[157] 1.0000000000000000000000 1.0000000000000000000000
[159] 1.0000000000000000000000 1.0000000000000000000000
[161] 1.0000000000000000000000 1.0000000000000000000000
[163] 1.0000000000000000000000 1.0000000000000000000000
[165] 1.0000000000000000000000 1.0000000000000000000000
[167] 1.0000000000000000000000 1.0000000000000000000000
[169] 1.0000000000000000000000 1.0000000000000000000000
[171] 1.0000000000000000000000 1.0000000000000000000000
[173] 1.0000000000000000000000 1.0000000000000000000000
[175] 1.0000000000000000000000 1.0000000000000000000000
[177] 1.0000000000000000000000 1.0000000000000000000000
[179] 1.0000000000000000000000 1.0000000000000000000000
[181] 1.0000000000000000000000 1.0000000000000000000000
[183] 1.0000000000000000000000 1.0000000000000000000000
[185] 1.0000000000000000000000 1.0000000000000000000000
[187] 1.0000000000000000000000 1.0000000000000000000000
[189] 1.0000000000000000000000 1.0000000000000000000000
[191] 1.0000000000000000000000 1.0000000000000000000000
[193] 1.0000000000000000000000 1.0000000000000000000000
[195] 1.0000000000000000000000 1.0000000000000000000000
[197] 1.0000000000000000000000 1.0000000000000000000000
[199] 1.0000000000000000000000 1.0000000000000000000000
[201] 1.0000000000000000000000 1.0000000000000000000000
[203] 1.0000000000000000000000 1.0000000000000000000000
[205] 1.0000000000000000000000 1.0000000000000000000000
[207] 1.0000000000000000000000 1.0000000000000000000000
[209] 1.0000000000000000000000 1.0000000000000000000000
[211] 1.0000000000000000000000 1.0000000000000000000000
[213] 1.0000000000000000000000 1.0000000000000000000000
[215] 1.0000000000000000000000 1.0000000000000000000000
[217] 1.0000000000000000000000 1.0000000000000000000000
[219] 1.0000000000000000000000 1.0000000000000000000000
[221] 1.0000000000000000000000 1.0000000000000000000000
[223] 1.0000000000000000000000 1.0000000000000000000000
[225] 1.0000000000000000000000 1.0000000000000000000000
[227] 1.0000000000000000000000 1.0000000000000000000000
[229] 1.0000000000000000000000 1.0000000000000000000000
[231] 1.0000000000000000000000 1.0000000000000000000000
[233] 1.0000000000000000000000 1.0000000000000000000000
[235] 1.0000000000000000000000 1.0000000000000000000000
[237] 1.0000000000000000000000 1.0000000000000000000000
[239] 1.0000000000000000000000 1.0000000000000000000000
[241] 1.0000000000000000000000 1.0000000000000000000000
[243] 1.0000000000000000000000 1.0000000000000000000000
[245] 1.0000000000000000000000 1.0000000000000000000000
[247] 1.0000000000000000000000 1.0000000000000000000000
[249] 1.0000000000000000000000 1.0000000000000000000000
[251] 1.0000000000000000000000 1.0000000000000000000000
[253] 1.0000000000000000000000 1.0000000000000000000000
[255] 1.0000000000000000000000 1.0000000000000000000000
[257] 1.0000000000000000000000 1.0000000000000000000000
[259] 1.0000000000000000000000 1.0000000000000000000000
[261] 1.0000000000000000000000 1.0000000000000000000000
[263] 1.0000000000000000000000 1.0000000000000000000000
[265] 1.0000000000000000000000 1.0000000000000000000000
[267] 1.0000000000000000000000 1.0000000000000000000000
[269] 1.0000000000000000000000 1.0000000000000000000000
[271] 1.0000000000000000000000 1.0000000000000000000000
[273] 1.0000000000000000000000 1.0000000000000000000000
[275] 1.0000000000000000000000 1.0000000000000000000000
[277] 1.0000000000000000000000 1.0000000000000000000000
[279] 1.0000000000000000000000 1.0000000000000000000000
[281] 1.0000000000000000000000 1.0000000000000000000000
[283] 1.0000000000000000000000 1.0000000000000000000000
[285] 1.0000000000000000000000 1.0000000000000000000000
[287] 1.0000000000000000000000 1.0000000000000000000000
[289] 1.0000000000000000000000 1.0000000000000000000000
[291] 1.0000000000000000000000 1.0000000000000000000000
[293] 1.0000000000000000000000 1.0000000000000000000000
[295] 1.0000000000000000000000 1.0000000000000000000000
[297] 1.0000000000000000000000 1.0000000000000000000000
[299] 1.0000000000000000000000 1.0000000000000000000000
[301] 1.0000000000000000000000 1.0000000000000000000000
[303] 1.0000000000000000000000 1.0000000000000000000000
[305] 1.0000000000000000000000 1.0000000000000000000000
[307] 1.0000000000000000000000 1.0000000000000000000000
[309] 1.0000000000000000000000 1.0000000000000000000000
[311] 1.0000000000000000000000 1.0000000000000000000000
[313] 1.0000000000000000000000 1.0000000000000000000000
[315] 1.0000000000000000000000 1.0000000000000000000000
[317] 1.0000000000000000000000 1.0000000000000000000000
[319] 1.0000000000000000000000 1.0000000000000000000000
[321] 1.0000000000000000000000 1.0000000000000000000000
[323] 1.0000000000000000000000 1.0000000000000000000000
[325] 1.0000000000000000000000 1.0000000000000000000000
[327] 1.0000000000000000000000 1.0000000000000000000000
[329] 1.0000000000000000000000 1.0000000000000000000000
[331] 1.0000000000000000000000 1.0000000000000000000000
[333] 1.0000000000000000000000 1.0000000000000000000000
[335] 1.0000000000000000000000 1.0000000000000000000000
[337] 1.0000000000000000000000 1.0000000000000000000000
[339] 1.0000000000000000000000 1.0000000000000000000000
[341] 1.0000000000000000000000 1.0000000000000000000000
[343] 1.0000000000000000000000 1.0000000000000000000000
[345] 1.0000000000000000000000 1.0000000000000000000000
[347] 1.0000000000000000000000 1.0000000000000000000000
[349] 1.0000000000000000000000 1.0000000000000000000000
[351] 1.0000000000000000000000 1.0000000000000000000000
[353] 1.0000000000000000000000 1.0000000000000000000000
[355] 1.0000000000000000000000 1.0000000000000000000000
[357] 1.0000000000000000000000 1.0000000000000000000000
[359] 1.0000000000000000000000 1.0000000000000000000000
[361] 1.0000000000000000000000 1.0000000000000000000000
[363] 1.0000000000000000000000 1.0000000000000000000000
[365] 1.0000000000000000000000 1.0000000000000000000000
[367] 1.0000000000000000000000 1.0000000000000000000000
[369] 1.0000000000000000000000 1.0000000000000000000000
[371] 1.0000000000000000000000 1.0000000000000000000000
[373] 1.0000000000000000000000 1.0000000000000000000000
[375] 1.0000000000000000000000 1.0000000000000000000000
[377] 1.0000000000000000000000 1.0000000000000000000000
[379] 1.0000000000000000000000 1.0000000000000000000000
[381] 1.0000000000000000000000 1.0000000000000000000000
[383] 1.0000000000000000000000 1.0000000000000000000000
[385] 1.0000000000000000000000 1.0000000000000000000000
[387] 1.0000000000000000000000 1.0000000000000000000000
[389] 1.0000000000000000000000 1.0000000000000000000000
[391] 1.0000000000000000000000 1.0000000000000000000000
[393] 1.0000000000000000000000 1.0000000000000000000000
[395] 1.0000000000000000000000 1.0000000000000000000000
[397] 1.0000000000000000000000 1.0000000000000000000000
[399] 1.0000000000000000000000 1.0000000000000000000000
[401] 1.0000000000000000000000 1.0000000000000000000000
[403] 1.0000000000000000000000 1.0000000000000000000000
[405] 1.0000000000000000000000 1.0000000000000000000000
[407] 1.0000000000000000000000 1.0000000000000000000000
[409] 1.0000000000000000000000 1.0000000000000000000000
[411] 1.0000000000000000000000 1.0000000000000000000000
[413] 1.0000000000000000000000 1.0000000000000000000000
[415] 1.0000000000000000000000 1.0000000000000000000000
[417] 1.0000000000000000000000 1.0000000000000000000000
[419] 1.0000000000000000000000 1.0000000000000000000000
[421] 1.0000000000000000000000 1.0000000000000000000000
[423] 1.0000000000000000000000 1.0000000000000000000000
[425] 1.0000000000000000000000 1.0000000000000000000000
[427] 1.0000000000000000000000 1.0000000000000000000000
[429] 1.0000000000000000000000 1.0000000000000000000000
[431] 1.0000000000000000000000 1.0000000000000000000000
[433] 1.0000000000000000000000 1.0000000000000000000000
[435] 1.0000000000000000000000 1.0000000000000000000000
[437] 1.0000000000000000000000 1.0000000000000000000000
[439] 1.0000000000000000000000 1.0000000000000000000000
[441] 1.0000000000000000000000 1.0000000000000000000000
[443] 1.0000000000000000000000 1.0000000000000000000000
[445] 1.0000000000000000000000 1.0000000000000000000000
[447] 1.0000000000000000000000 1.0000000000000000000000
[449] 1.0000000000000000000000 1.0000000000000000000000
[451] 1.0000000000000000000000 1.0000000000000000000000
[453] 1.0000000000000000000000 1.0000000000000000000000
[455] 1.0000000000000000000000 1.0000000000000000000000
[457] 1.0000000000000000000000 1.0000000000000000000000
[459] 1.0000000000000000000000 1.0000000000000000000000
[461] 1.0000000000000000000000 1.0000000000000000000000
[463] 1.0000000000000000000000 1.0000000000000000000000
[465] 1.0000000000000000000000 1.0000000000000000000000
[467] 1.0000000000000000000000 1.0000000000000000000000
[469] 1.0000000000000000000000 1.0000000000000000000000
[471] 1.0000000000000000000000 1.0000000000000000000000
[473] 1.0000000000000000000000 1.0000000000000000000000
[475] 1.0000000000000000000000 1.0000000000000000000000
[477] 1.0000000000000000000000 1.0000000000000000000000
[479] 1.0000000000000000000000 1.0000000000000000000000
[481] 1.0000000000000000000000 1.0000000000000000000000
[483] 1.0000000000000000000000 1.0000000000000000000000
[485] 1.0000000000000000000000 1.0000000000000000000000
[487] 1.0000000000000000000000 1.0000000000000000000000
[489] 1.0000000000000000000000 1.0000000000000000000000
[491] 1.0000000000000000000000 1.0000000000000000000000
[493] 1.0000000000000000000000 1.0000000000000000000000
[495] 1.0000000000000000000000 1.0000000000000000000000
[497] 1.0000000000000000000000 1.0000000000000000000000
[499] 1.0000000000000000000000 1.0000000000000000000000
Şimdi de hesaplanan bu kümülatif olasılık değerlerine göre kümülatif olasılık fonksiyonu (CDF:Cumulative Distribution Function)’nun grafiğini çizelim.Grafik başlığında belirtilen N, popülasyon büyüklüğünü, p her bir denemedeki başarı olasılığını ve s başarı denemelerin sayısı (size)’nı göstermektedir.

Yapılan bu çalışma ile özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına bir katkı sunulması amaçlanmıştır.
Daha önce kesikli olasılıklı dağılım türleri üzerine örnek uygulama yaptığım çalışmaların linklerini de aşağıda paylaşıyorum ilgilenenler için.
Bernoulli Olasılık Dağılımı Üzerine Bir Vaka Çalışması
Binom Olasılık Dağılımı Üzerine Bir Vaka Çalışması
Kesikli Uniform Olasılık Dağılımı Üzerine Bir Vaka Çalışması
Poisson Olasılık Dağılımı Üzerine Bir Vaka Çalışması
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
- https://pj.freefaculty.org/guides/stat/Distributions/DistributionWriteups/NegativeBinomial/NegativeBinomial.pdf
- https://planetcalc.com/7696/
- https://www.educator.com/media/qn-dl/probability-murray/Prob-14.pdf
- https://www.rdocumentation.org/packages/vcd/versions/1.4-7/topics/goodfit
- https://web.stanford.edu/class/bios221/labs/simulation/Lab_3_simulation.html
- http://kisi.deu.edu.tr/kemal.sehirli/%C4%B0STAT%C4%B0ST%C4%B0K%20I-VI.pdf
- https://en.wikipedia.org/wiki/Ladislaus_Bortkiewicz
- https://onlinelibrary.wiley.com/doi/abs/10.1111/insr.12083
- https://online.stat.psu.edu/stat504/node/169/
- https://cran.r-project.org/web/packages/ggpubr/ggpubr.pdf
- http://www.mas.ncl.ac.uk/~nag48/teaching/MAS1403/notes4.pdf
- https://tevfikbulut.com/2020/07/23/rda-poisson-ve-negatif-binom-regresyon-yontemleri-uzerine-bir-vaka-calismasi-a-case-study-on-poisson-and-negative-binomial-regression-methods-in-r/
- https://my.ilstu.edu/~wjschne/442/SimulatingRandomData.html#discrete-uniform-distribution
- https://en.wikipedia.org/wiki/Discrete_uniform_distribution
- http://www.hcs.harvard.edu/cs50-probability/binomial.php
- http://people.stern.nyu.edu/adamodar/New_Home_Page/StatFile/statdistns.htm
- https://statisticsglobe.com/bernoulli-distribution-in-r-dbern-pbern-qbern-rbern
- https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Distributions.html
- https://my.ilstu.edu/~wjschne/442/SimulatingRandomData.html#bernoulli-distribution
- https://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm
- RStudio Cloud: https://login.rstudio.cloud/
- Matematiksel İstatistik, İsmail Erdem, Gözden Geçirilmiş ve Genişletilmiş 3. Baskı.
- The R Project for Statistical Computing. https://www.r-project.org/
- Microsoft Office Excel 2010 Version, Microsoft Corporation. Technology company. Redmond, Washington, United States
- https://online.stat.psu.edu/stat504/node/57/#:~:text=The%20Poisson%20Model%20(distribution)%20Assumptions,the%20same%20for%20all%20teams.