Verinin Standartlaştırılması Üzerine Vaka Çalışmaları: Case Studies on Standardization of Data

Aralık 7 2020

Intro

The main focus of this study is the practical handling of some standardization methods that have found application in the literature.The standardization methods commonly used in the literature are as follows:

  1. Z-Score Standardization
  2. Standardization with a Distribution Range of 1
  3. Standardization with a Distribution Range (-1;+1)
  4. Standardization with a Distribution Range (0;+1)
  5. Standardization with Maximum Value of 1
  6. Standardization to Arithmetic Mean 1
  7. Standardization with a Standard Deviation of 1

Giriş

Veri bilimciler ve veri mühendisleri çok değişkenli istatistiksel analizler üzerinde yoğun bir şekilde çalışmaktadır. Ancak bazı durumlarda seçilen analiz yönteminin ilk varsayımlarının yerine getirilmesi gerekmektedir. Bu varsayımlardan ve gerekliliklerden biri de veri setinin standartlaştırılmasıdır. Örnek vermek gerekirse küme analizleri başta olmak üzere yapay sinir ağları alanlarında da standartlaştırmanın kendine uygulama alanı bulduğu görülmektedir. Peki standartlaştırma neden gereklidir? Verinin standardize edilmek istenmesinin temel sebebi verinin aynı ölçü birimine indirgenmesidir. Ancak bu indirgeme işlemi verinin dönüştürülmesi veya dönüşümü ile özellikle karıştırılmaması gerekir. Veri standardize edildiğinde yani aynı ölçü birimine indirgendiğinde dağılım şekli değişmemektedir. Değişen tek şey burada ölçü birimidir. Verinin dönüştürülmesi işleminde ise istatistiksel dağılımın şekli de değişir. Bu işlem ise genelde verinin dağılım şeklini analizi yapılacak yöntemin benimsediği dağılım şekline dönüştürmek için yapılır. Verinin dağılım şekline göre farklı dönüşüm metotları uygulanabilmektedir. Örneğin analize geçmeden önce veri aşırı pozitif çarpıksa log dönüşümünün yaygın kullanıldığı görülmektedir . Bu çalışma kapsamında verinin dönüşümü ele alınmayacaktır. Dolayısıyla verinin dönüşümü konusuna ayrıntılı bir giriş yapılmamıştır. Bu çalışmanın ana odağı, literatürde kendine uygulama alanı bulan bazı standartlaştırma yöntemlerini uygulamalı örnekler üzerinden adım adım irdelemektir. Literatürde ağırlıklı olarak kullanılan standartlaştırma yöntemleri şöyledir:

  1. Z Skor Standartlaştırma
  2. Dağılım Aralığı 1 Olacak şekilde Standartlaştırma
  3. Dağılım Aralığı (-1;+1) Olacak şekilde Standartlaştırma
  4. Dağılım Aralığı (0;+1) Olacak şekilde Standartlaştırma
  5. En Büyük Değer 1 Olacak şekilde Standartlaştırma
  6. Aritmetik Ortalama 1 Olacak Şekilde Standartlaştırma
  7. Standart Sapma 1 Olacak Şekilde Standartlaştırma

Yüklenen Kütüphaneler

library<-c("dplyr","tibble","tidyr","ggplot2","formattable","readr","readxl","ggpubr","formattable", "ggstance","scales", "rmarkdown", "knitr","writexl", "kableExtra")
loading<-sapply(library, require, character.only = TRUE)
loading

Tesadüfi sentetik (hipotetik) veri üretme

Bu kısımda tek değişkenli ve 1000 (N) gözlemden oluşan bir veri seti, basit tekrarlı örneklem yöntemi kullanılarak üretilecektir. Üretilen veri setinde beden kitle endeksi (BKİ) alt ve üst sınır değerleri (alt sınır=18,5, üst sınır=40) modellenmiştir.

set.seed(61)#aynı sonuçları almak için
bki=seq(18.499, 40.001, 0.001)
N=sample(bki, 1000, replace=TRUE)
veri=tibble(x=N)
veri %>% head(10) %>% formattable() #ilk 10 gözlem

Tanımlayıcı istatistikler

summary(veri)

       x        
 Min.   :18.51  
 1st Qu.:23.71  
 Median :28.98  
 Mean   :29.13  
 3rd Qu.:34.30  
 Max.   :39.98

Z Skor Standartlaştırma

Z skor standartlaştırma, veri setindeki gözlem değerlerinin ortalaması 0, standart sapması 1 olan yeni veri setine dönüştürülmesidir. Z skoru= (x-xort)/sd. Bu işlem Microsoft Excel’de =STANDARTLAŞTIRMA (x, ortalama, standart_sapma) fonksiyonu ile de yapılmaktadır. Bu ve buna benzer fonksiyonlar bilinmese de diğer yöntemler gibi formülleri kolayca Excel ortamında uygulanabilir. Diğer bir ifadeyle, bahsedilecek diğer standartlaştırma yöntemlerinin de Microsoft Excel ortamında yapılması gayet kolay ve mümkündür. Bunu R programlama dili bilmeyenler için özellikle ifade etmek gerekir. Burada R programlama dilinin bu konu alanında Microsoft Excel’e göre üstün yanı yüksek gözlem sayısına sahip veri setlerinde ortaya çıkmaktadır. R ve diğer açık kaynak programlama dilleri büyük veri setleri üzerinde çalışılması açısından Microsoft Excel gibi paket programlara göre daha esnek, daha hızlı ve gelişmiştir.

tibble(bki=veri$x, bki_zskor=scale(veri$x)) %>% head(10) %>% formattable() #ilk 10 gözlem

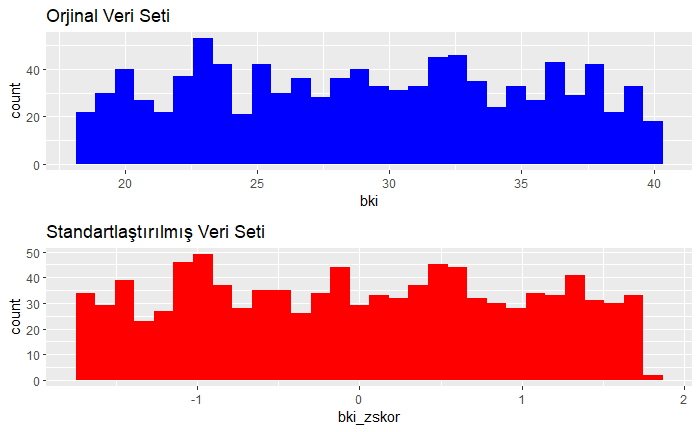
Z Skor Standartlaştırma: Histogramların Karşılaştırılması

Burada standartize edilen veri seti ile standartize edilmemiş veri setinin dağılımı histogramla karşılaştırılmıştır. Görüleceği üzere dağılımın şekli değişmemiştir.

df=tibble(bki=veri$x, bki_zskor=scale(veri$x))
v1<-ggplot(df, aes(x=bki)) +
  geom_histogram(fill="blue")+
  ggtitle("Orjinal Veri Seti")
v2<-ggplot(df, aes(x=bki_zskor)) +
  geom_histogram(fill="red")+
  ggtitle("Standartlaştırılmış Veri Seti")
ggarrange(v1,v2, ncol = 1)

Dağılım Aralığı 1 Olacak şekilde Standartlaştırma

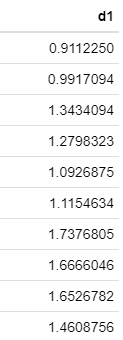
Her bir değer dağılım aralığına bölünerek hesaplanır. Dağılım aralığı= Mak-Min.

tibble(d1=veri$x/(max(veri$x)-min(veri$x))) %>% head(10) %>% formattable() #ilk 10 gözlem

Dağılım Aralığı (-1;+1) Olacak şekilde Standartlaştırma

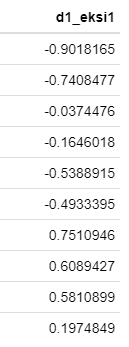
(x-(xmak+xmin)/2)/(xmak-xmin)/2 eşitliği ile hesaplanır.

m=veri$x-(max(veri$x)+min(veri$x))/2 # eşitliğin payı
x=(max(veri$x)-min(veri$x))/2 # eşitliğin paydası

tibble(d1=m/x) %>% head(10) %>% formattable() #ilk 10 gözlem

En Büyük Değer 1 Olacak şekilde Standartlaştırma

x/xmax eşitliği ile hesaplanır.

tibble(mak1=veri$x/max(veri$x)) %>% head(10) %>% formattable() #ilk 10 gözlem

Aritmetik Ortalama 1 Olacak şekilde Standartlaştırma

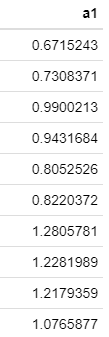
x/xort eşitliği ile hesaplanır.

tibble(a1=veri$x/mean(veri$x)) %>% head(10) %>% formattable() #ilk 10 gözlem

Dağılım Aralığı (0;+1) Olacak şekilde Standartlaştırma

(x-xmin)/ (xmak-xmin) eşitliği ile hesaplanır. Dağılım aralığı= Mak-Min.

tibble(dsifir_bir=(veri$x-min(veri$x))/(max(veri$x)-min(veri$x))) %>% head(10) %>% formattable() #ilk 10 gözlem

Standart Sapması 1 Olacak şekilde Standartlaştırma

x/xsd eşitliği ile hesaplanır.

tibble(sd_1=veri$x/sd(veri$x)) %>% head(10) %>% formattable() #ilk 10 gözlem

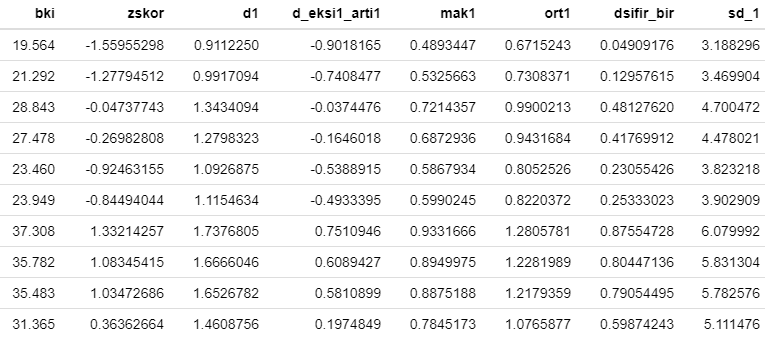
Özet: Yönteme Göre Standartlaştırılmış Değerler ve Orjinal Veri Seti

tum=tibble(bki=N) %>% mutate(zskor=scale(veri$x),d1=veri$x/(max(veri$x)-min(veri$x)),d_eksi1_arti1=m/x,mak1=veri$x/max(veri$x), ort1=veri$x/mean(veri$x),dsifir_bir=(veri$x-min(veri$x))/(max(veri$x)-min(veri$x)),sd_1=veri$x/sd(veri$x)) 

#ilk 10 gözlem

tum %>% head(10) %>% formattable()

Sonuçların Microsoft Excel Kitabına Yazdırılması

write_xlsx(tum, "tum_sonuclar.xlsx")

Yukarıdaki kod bloğunun çalıştırılmasından sonra sonuçlar Microsoft Excel uzantılı (xlsx) çalışma kitabına yazdırılmış olup, aşağıdaki linkten sonuçları indirebilirsiniz.

Yönteme Göre Tüm Sonuçlarİndir

Sonuç

Yapılan uygulamalı çalışmayla verinin standartlaştırılması konusu özelinde farkındalık oluşturulması amaçlanmıştır.

Faydalı olması dileğiyle.

Yararlanılan Kaynaklar

  • Beden Kitle Endeksi Referans Değerleri. https://www.acibadem.com.tr/ilgi-alani/vucut-kitle-indeksi-hesaplama/#genel-tanitim
  • RStudio Cloud: https://login.rstudio.cloud/
  • The R Project for Statistical Computing. https://www.r-project.org/
  • Alpar, R. (2017). Uygulamalı Çok Değişkenli İstatistiksel Yöntemler. 5. Baskı. Detay Yayıncılık.
  • https://support.microsoft.com/tr-tr/office/standartla%C5%9Ftirma-i%C5%9Flevi-81d66554-2d54-40ec-ba83-6437108ee775
  • Verinin Standartlaştırılması Üzerine Vaka Çalışmaları. https://rpubs.com/tevfik1461/vs3
Önceki yazı Sonraki Yazı

Yorum Yaz