Giriş
Topluluk (ensemble) öğrenme algoritmaları tahmine dayalı analitik çalışmalarda en başarılı yaklaşımlardan biridir. Bu algoritmalar somut bir problemi çözmek için bir araya gelen modeller setinden oluşmaktadır. Amaç modeller setinin ürettiği tahminleri birleştirerek doğruluğu (accuracy) artırmaktır. Topluluk algoritmaları kendi içerisinde üç grupta ele alınır.
- Torbalama (Bagging: Bootsrap Aggregating)
- Artırma (Boosting)
- İstif (Stacking)
Topluluk (ensemble) öğrenme algoritmalarından biri olan torpalama, ingilizce ifadeyle Bagging, Breiman tarafından 1994 yılında geliştirilen hem sınıflandırma hem de regresyon problemlerinin çözümünde kullanılan makine öğrenmesine dayanan topluluk algoritmasıdır. Torbalama algoritmasının işleyiş süreci Şekil 1’de verilmiştir.
Şekil 1: Torbalama (Bagging) Algoritmasının İşleyiş Süreci

Şekil 1’de belirtilen torbalama algoritmasının işleyiç sürecini adım adım şöyle özetleyebiliriz.
- Popülasyon (N) birimlerini eğitilecek (training) veri setine ve test edilecek (testing) veri setine basit tekrarsız tesadüfi örnekleme (simple random sampling without replacement) yöntemiyle ayrılır. Burada literatürde genellikle eğitilecek veri seti seti için popülasyonun % 70’i alınsa da bu oran veri setinin ya da popülasyonun büyüklüğüne göre değişkenlik gösterebilmektedir. Bu oran 70:30 olabileceği gibi, 60:40 veya 80:20 oranı şeklinde de olabilir.
- Eğitilecek veri setini belirledikten sonra basit tekrarlı tesadüfi örnekleme yoluyla torbalara (1’den n’e kadar) örneklem birimleri (sample units) atanır.
- Örneklem birimleri kurulan modellerde eğitilir.
- Regresyon problemini çözüyorsak kurulan modellerden elde edilen sonuçların ortalaması alınarak bağımlı değişken (y) belirlenir. Sınıflandırma problemi çözüyorsak kurulan modellerden elde edilen çoğunluk oylama sonuçlarına göre karar verip y’yi, diğer bir ifadeyle bağımlı değişkeni (dependent variable) tahmin etmiş oluruz.
Modeller oluşturulurken temel amaç, bias ve varyans dengesinin kurulmasıdır. Bu uyumu sağlarsak iyi model uyumu (good-fit) elde etmiş oluruz. Makine öğrenme ve derin öğrenme problemlerinin çözümünde modelleme hatalarına bağlı olarak varyans ve bias değişiklik göstermektedir. Bu iki durum şöyle ele alınabilir:
- Eksik model uyumu (under-fitting): Kurulan modelde elde edilen tahmin değerleri gözlem verisine yeterince uyum göstermediğinde ortaya çıkar. Bu durumda varyans düşükken bias yüksektir. Buradan şunu anlamak gerekir: gözlem verisi ile tahmin edilen veri arasındaki fark büyükse, diğer bir deyişle kurulan modelle bağımlı değişken iyi tahmin edilemiyorsa bu durumda under-fitting oluşur. Under-fitting sonraki kısımlarında anlatılan sınıflandırma ve regresyon hata metrikleri ile kolaylıkla ortaya konulabilir.
- Aşrı model uyumu (over-fitting): Kurulan modelde eğitilen veri seti (training data set)’yle gözlem verisine aşırı uyum gösterdiğinde ortaya çıkar. Bu durumda varyans yüksekken bias düşüktür.
Bahsedilen bu iki durumu kafamızda daha da canlı tutmak için bias ve varyans ilişkisi Şekil 2’de verilmiştir. Şekil’de biz modeli kurgularken olması gereken durumu gösteren Düşük Varyans-Düşük Bias uyumunu hedefliyoruz. Diğer bir ifadeyle, kurguladığımız model (Şekil 2 1 nolu model) ile gözlem değerlerini olabildiğince en yüksek doğruluk oranı ile tahmin ederken aynı zamanda varyansı düşük tutmayı hedefliyoruz. Buna başardığımızda aslında iyi model uyumunu (good-fit) sağlamış ve iyi bir model kurmuş oluyoruz. Eksik model uyumu (under-fitting)’nda ise Şekil 2’de 3 nolu modelde görüleceği üzere elde edilen tahmin değerleri gözlem değerleri (kırmızı alan)’nden uzaklaşmakla birlikte hala tahmin değerleri ile gözlem değerleri arasında farklar, diğer bir deyişle varyans düşüktür. Aşırı model uyumu (over-fitting)’da ise Şekil 2’de 2 nolu modelde görüleceği üzere varyan yüksek iken bias düşüktür. 2 nolu modelde doğru değerler (gözlem değerleri)’i kurulan modelde yüksek doğrulukla (düşük bias) tahmin edilse de gözlem değerleri ile tahmin değerleri arasındaki varyans yüksektir.
Şekil 2: Bias-Varyans İlişkisi

Veri Tipleri
Torbalama yöntemi ile sınıflandırma problemi çözüyorsak bağımlı değişkenin ya da cevap değişkeninin veri tipi nitel ve kategoriktir. Ancak, bu yöntem ile regresyon problemini çözüyorsak bağımlı değişkenin ya da cevap değişkeninin veri tipi niceldir. Veri tipleri kendi içerisinde 4 farklı alt sınıfta ele alınabilir. Bu veri tipleri alt sınıflarıyla birlikte Şekil 3’te verilmiştir.
Şekil 3: Veri Tipleri
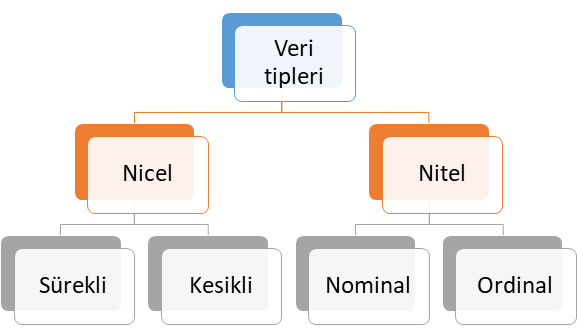
Nicel Veri (Quantitative Data)
Şekil 3’te sunulan nicel veri tipi ölçülebilen veri tipi olup, kendi içerisinde temel olarak ikiye ayrılmaktadır. Bu veri tipine alt sınıflandırmalar dikkate alınarak sırasıyla örnek verelim.
- Sürekli veri (Continous data): Tam sayı ile ifade edilmeyen veri tipi olup, zaman, sıcaklık, beden kitle endeksi, boy ve ağırlık ölçümleri bu veri tipine örnek verilebilir.
- Kesikli veri (Discrete Data): Tam sayı ile ifade edilebilen veri tipi olup, bu veri tipine proje sayısı, popülasyon sayısı, öğrenci sayısı örnek verilebilir.
Nitel Veri (Qualitative Data)
Şekil 3’te verilen nitel veri tipi ölçülemeyen ve kategori belirten veri tipi olup, kendi içerisinde temel olarak ikiye ayrılmaktadır. Bu veri tipine alt sınıflandırmalar şöyledir:
- Nominal veri: İki veya daha fazla cevap kategorisi olan ve sıra düzen içermeyen veri tipi olup, bu veri tipine medeni durum (evli, bekar) ve sosyal güvenlik türü (Bağkur, SSK, Yeşil Kart, Özel Sigorta) örnek gösterilebilir.
- Ordinal veri: İki veya daha fazla kategorisi olan ancak sıra düzen belirten veri türüdür. Bu veri tipine örnek olarak eğitim düzeyleri (İlkokul, ortaokul, lise, üniversite ve yüksek lisans), yarışma dereceleri (1. , 2. ve 3.) ve illerin gelişmişlik düzeyleri (1. Bölge, 2. Bölge, 3. Bölge, 4. Bölge, 5. Bölge ve 6. Bölge) verilebilir.
Veri tiplerinden bahsedildikten sonra bu veri tiplerinin cevap değişkeni (bağımlı değişken) olduğu durumlarda seçilecek analiz yöntemini ele alalım. Temel olarak cevap değişkeni ölçülebilir numerik değişken ise regresyon, değilse sınıflandırma analizi yapıyoruz. Cevap değişkeni, diğer bir deyişle bağımlı değişken numerik ise bağımsız değişken veya değişkenlerin çıktı (output) / bağımlı değişken (dependent variable) / hedef değişken (target variable) veya değişkenlerin üzerindeki etkisini tahmin etmeye çalışıyoruz. Buradaki temel felsefeyi anlamak son derece önemlidir. Çünkü bu durum sizin belirleyeceğiniz analiz yöntemini de değiştirecektir.
Kullanılan analiz yöntemi ile kurulan modelde ya sınıflandırma problemini ya da regresyon problemini çözdüğümüzü ifade etmiştik. Ancak kurulan modellerde çözülen problemin sınıflandırma ya da regresyon oluşuna göre performans değerlendirmesi farklılaşmaktadır. Sınıflandırma problemlerinde kullanılan hata metrikleri ile regresyon hata metrikleri aynı değildir. Bu bağlamda ilk olarak sınıflandırma problemlerinin çözümünde kullanılan hata metriklerini ele alalım.
Sınıflandırma Problemlerinde Hata Metrikleri
Karışıklık matrisi (confusion matrix) olarak olarak adlandırılan bu matris sınıflandırma problemlerinin çözümünde hata metriklerini ortaya koyarak kurulan modelin veya modellerin hata oranını değerlendirmektedir. Hata matrisinin makine ve derin öğrenme metotlarının değerlendirilmesinde sıklıkla kullanıldığı görülmektedir. Tablo 1’de hata metriklerinin hesaplanmasına esas teşkil eden karışıklık matrisi (confisioun matrix) verilmiştir. Bu tabloyla sınıflandırma hataları hesaplanabilmektedir. Tabloda yer verilen Tip 1 hata (Type 1 error) istatistikte alfa hatasını göstermektedir. Tip 1 hata H0 hipotezi (null hpypothesis) doğru olduğu halde reddedilmesidir. Tabloda Tip 2 hata (Type II error) olarak adlandırılan hata ise istatistikte Beta hatası olarak da bilinmektedir. Tip 2 hata ise H0 hipotezi (null hpypothesis) yanlış olduğu halde kabul edilmesidir.
Tablo 1: Karışıklık Matrisi (Confusion Matrix)

Tablo 1’de TP: Doğru Pozitifleri, FN: Yanlış Negatifleri, FP: Yanlış Pozitifleri ve TN: Doğru Negatifleri göstermektedir.
Şekil 3’te de yer verildiği üzere literatürde sınıflandırma modellerinin performansını değerlendirmede aşağıdaki hata metriklerinden yaygın bir şekilde yararlanıldığı görülmektedir. Sınıflandırma problemlerinin çözümüne yönelik Rastgele Orman Algoritması (RF) kullanarak R’da yapmış olduğum çalışmanın linkini ilgilenenler için aşağıda veriyorum.
- Doğruluk (Accuracy): TP+TN / TP+TN+FP+FN eşitliği ile hesaplanır. Modelin genel performansını ortaya koyar. Bu sınıflandırma metriği ile aslında biz informal bir şekilde dile getirirsek doğru tahminlerin toplam tahminler içindeki oranını hesaplamış oluyoruz.
- Kesinlik (Precision): TP / TP+FP eşitliği ile hesaplanır. Doğru tahminlerin ne kadar kesin olduğunu gösterir.
- Geri çağırma (Recall): TP / TP+FN eşitliği ile hesaplanır. Gerçek pozitif örneklerin oranını verir.
- Özgünlük (Specificity): TN / TN+FP eşitliği ile hesaplanır. Gerçek negatif örneklerin oranını gösterir.
- F1 skoru : 2TP / 2TP+FP+FN eşitliği ile hesaplanır. Dengesiz sınıflar için yararlı hibrit bir metrik olup, kesinlik (precision) ve geri çağırma (recall) skorlarının ağırlıklı ortalamasını ifade etmektedir.
- ROC (Receiver operating characteristic): Yukarıda karışıklık matrisinde belirtilen parametrelerden yararlanılarak hesaplanır. ROC eğrisi olarak da adlandırılmaktadır. ROC eğrileri, herhangi bir tahmin modelinin doğru pozitifler (TP) ve negatifler (TN) arasında nasıl ayrım yapabileceğini görmenin güzel bir yoludur. Sınıflandırma modellerin perfomansını eşik değerler üzerinden hesaplar. ROC iki parametre üzerinden hesaplanır. Doğru Pozitiflerin Oranı (TPR) ve Yanlış Pozitiflerin Oranı (FPR) bu iki parametreyi ifade eder. Burada aslında biz TPR ile Geri Çağırma (Recall), FPR ile ise 1-Özgünlük (Specificity)‘ü belirtiyoruz.
- Cohen Kappa: Kategorik cevap seçenekleri arasındaki tutarlılığı ve uyumu gösterir. Cohen, Kappa sonucunun şu şekilde yorumlanmasını önermiştir: ≤ 0 değeri uyumun olmadığını, 0,01–0,20 çok az uyumu, 0,21-0,40 az uyumu, 0,41-0,60 orta, 0,61-0,80 iyi uyumu ve 0,81–1,00 çok iyi uyumu göstermektedir. 1 değeri ise mükemmel uyum anlamına gelmektedir.
Regresyon Problemlerinde Hata Metrikleri
Regresyon modellerinin performansını değerlendirmede literatürde aşağıdaki hata metriklerinden yaygın bir şekilde yararlanılmaktadır. Regresyon metrikleri eştiliklerinin verilmesi yerine sade bir anlatımla neyi ifade ettiği anlatılacaktır. Böylece formüllere boğulmamış olacaksınız.
- SSE (Sum of Square Error): Tahmin edilen değerler ile gözlem değerleri arasındaki farkların kareleri toplamını ifade eder.
- MSE (Mean Square Error): Ortalama kare hatası olarak adlandırılan bu hata tahmin edilen değerler ile gözlem değerleri arasındaki farkların karelerinin ortalamasını ifade eder.
- RMSE (Root Mean Square Error): Kök ortalama kare hatası olarak adlandırılan bu hata ortalama kare hatasının karekökünü ifade etmektedir.
- MAE (Mean Absolute Error): Ortalama mutlak hata olarak adlandırılan bu hata türü ise tahmin edilen değerler ile gözlem değerleri arasındaki farkların mutlak değerlerinin ortalamasını ifade etmektedir.
- MAPE (Mean Absolute Percentage Error): Ortalama mutlak yüzdesel hata olarak adlandırılan bu hata türünde ilk olarak tahmin edilen değerler ile gözlem değerleri arasındaki farkların mutlak değerleri hesaplanır. Daha sonra hesaplanan farkları mutlak değerleri mutlak değerleri alınan gözlem değerlerine bölünür. En son durumda ise elde edilen bu değerlerin ortalaması alınır.
- Bias: Tahmin edilen değerler ile gözlem değerleri arasındaki farkların ortalamasıdır. Bu yönüyle ortalama mutlak hata (MAE)’ya benzemektedir.
Regresyon hata metriklerini anlattıktan sonra daha kalıcı olması ve öğrenilmesi adına hazırladığım excel üzerinde bahsedilen bu metriklerin nasıl hesaplandığı gösterilmiştir. Excel dosyasını aşağıdaki linkten indirebilirsiniz.
Çalışma kapsamında torbalama algoritmasıyla regresyon problemi çözülecektir. Bu amaçla ABD’nin Boston bölgesi konut fiyatları veri seti kullanılarak bağımlı değişken olan konutların medyan fiyatları tahmin edilecektir.
Metodoloji ve Uygulama Sonuçları
Bu bölümde torbalama algoritması kullanılarak ABD’nin Boston bölgesinde konutların medyan fiyatları (hedef değişken) tahmin edilmiştir. Diğer bir ifadeyle, bu çalışmada regresyon problemi çözmüş olacağız. Analizde kullanılan veri seti ABD Nüfus Bürosu tarafından Boston bölgesindeki konutlarla ilgili olarak toplanan verilerden oluşmaktadır. Veri setindeki toplam gözlem sayısı 506, değişken sayısı ise 14’tür. Bu veri setine R programlama yazılımında “mlbench” paketi içerisinde “BostonHousing” olarak yer verilmiştir. R programlama dili kullanılarak torbalama (bagging) algoritmasıyla analiz edilmiştir. Veri setinde yer alan değişkenler ve değişkenlerin veri tipleri şöyledir:
- crim: per capita crime rate by town. Veri tipi nicel ve süreklidir.
- zn: proportion of residential land zoned for lots over 25,000 sq.ft. Veri tipi nicel ve kesiklidir.
- indus: proportion of non-retail business acres per town. Veri tipi nicel ve süreklidir.
- chas: Charles River dummy variable (1 if tract bounds river; 0 otherwise). Veri tipi nitel ve nominal kategoriktir.
- nox: nitric oxides concentration (parts per 10 million): Veri tipi nicel ve süreklidir.
- rm: average number of rooms per dwelling. Veri tipi nicel ve süreklidir.
- age: proportion of owner-occupied units built prior to 1940. Veri tipi nicel ve süreklidir.
- dis: weighted distances to five Boston employment centres. Veri tipi nicel ve kesiklidir.
- rad: index of accessibility to radial highways. Veri tipi nicel ve süreklidir.
- tax: full-value property-tax rate per $10,000. Veri tipi nicel ve kesiklidir.
- ptratio: pupil-teacher ratio by town. Veri tipi nicel ve süreklidir.
- b: 1000(Bk – 0.63)^2 where Bk is the proportion of blacks by town. Veri tipi nicel ve süreklidir.
- lstat: % lower status of the population. Veri tipi nicel ve süreklidir.
- medv: Median value of owner-occupied homes in $1000’s. Veri tipi nicel ve süreklidir.
Bu kapsamda cevap değişkeni (bağımlı değişken) olan “medv” yani konut fiyatlarının medyan değeri geri kalan 13 bağımsız değişken kullanılarak torbalama algoritmasıyla tahmin edilecektir. Analizde kullanılan veri setini aşağıdaki linkten indirebilirsiniz.
Şimdi veri setini tanıdıktan sonra adım adım (step by step) analize başlayabiliriz. Analizde R programlama dili kullanarak analiz adımları R kod bloklarında verilmiştir.
Yüklenecek R kütüphaneleri
rm(list=ls())
kütüphaneler = c("dplyr","tibble","tidyr","ggplot2","formattable","readr","readxl","xlsx", "pastecs","fpc", "DescTools","e1071", "DMwR", "metrics","caret", "mlbench", "viridis","GGally","ggpurr","psych","writexl","ggfortify","explore", "rattle","yardstick","MASS", "ipred", "performanceEstimation")
sapply(kütüphaneler, require, character.only = TRUE)
Ver setinin okunması
data(BostonHousing)
veri<-BostonHousing
Ver setinin xlsx dosyasına yazdırılması
write_xlsx(veri, "Bostonkonutfiyatları.xlsx")#xlsx dosyası için
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri seti xlsx uzantılı dosyaya yazdırılmıştır. Elde edilen veri seti dosyası xlsx uzantılı olarak aşağıdan indirilebilir.
Veri setinin görselleştirilmesi ve tanımlayıcı istatistikler
#veri setindeki ilk 3 değişkenin görselleştirilmesi
veri[,1:3] %>% explore_all()
#veri setindeki 4,5,6 ve 7. değişkenlerin görselleştirilmesi
veri[,4:7] %>% explore_all()
#veri setindeki 8,9 ve 10. değişkenlerin görselleştirilmesi
veri[,8:10] %>% explore_all()
#veri setindeki 11,12,13 ve 14. değişkenlerin görselleştirilmesi
veri[,11:14] %>% explore_all()
#veri setindeki ilk 10 gözlem
formattable(head(veri,10))
#Pearson korelasyon matrisi
cor.plot(veri[,-4], main="Korelasyon Matrisi")
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki ilk 3 değişkenin grafiği aşağıda verilmiştir. Grafikte görüleceği üzere eksik gözlem (missing data: NA) bulunmamaktadır.

Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki 4,5,6 ve 7. değişkenlerin grafiği aşağıda verilmiştir. Grafikte görüleceği üzere eksik gözlem (missing data: NA) bulunmamaktadır.

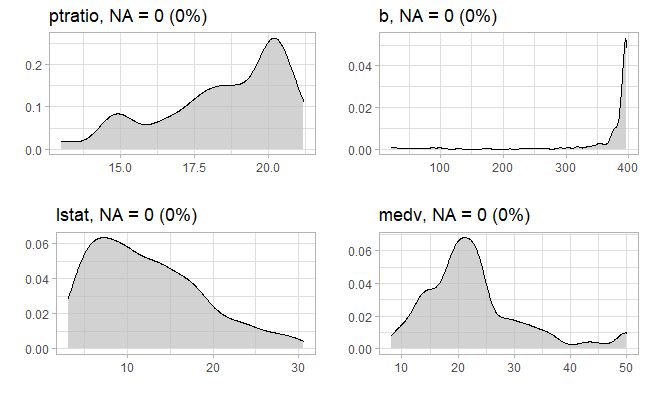
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki 8,9 ve 10. değişkenlerin grafiği aşağıda verilmiştir. Grafikte görüleceği üzere eksik gözlem (missing data: NA) bulunmamaktadır.
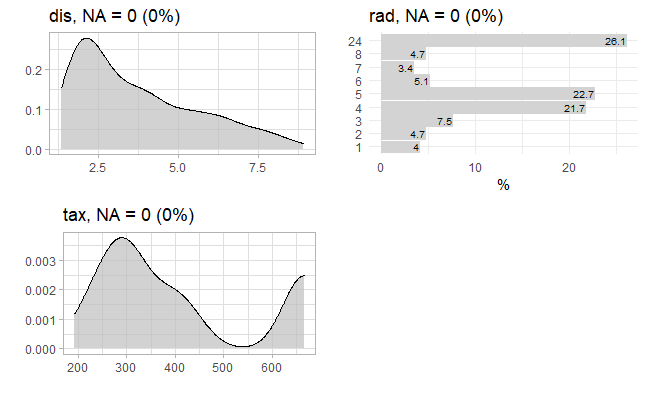
Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki 11, 12, 13 ve 14. değişkenlerin grafiği aşağıda verilmiştir. Grafikte görüleceği üzere eksik gözlem (missing data: NA) bulunmamaktadır.
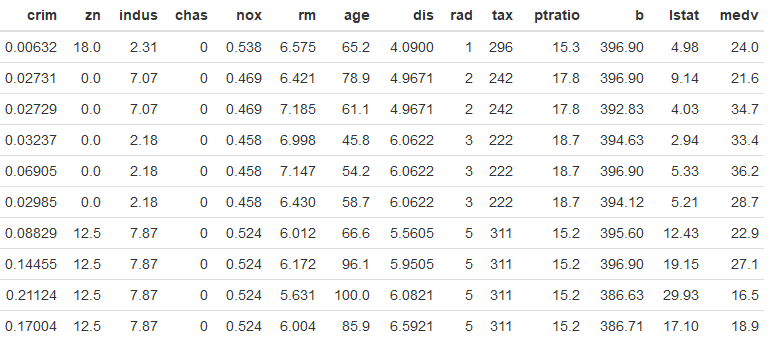
Yukarıdaki R kod bloğunun çalıştırılmasından sonra Boston Konut Fiyatları veri setindeki ilk 10 gözlem aşağıdaki tabloda verilmiştir.
Yukarıdaki R kod bloğunun çalıştırılmasından sonra nicel ve kesikli değişkenlere ait Pearson korelasyon matrisi aşağıdaki şekilde verilmiştir. Değişken çiftleri nicel (sürekli ve kesikli) olduğu için Pearson korelasyon katsayılarını hesapladık.

Veri setinin eğitilecek veri setine ve test veri setine ayrılması
Bu kısımda aşağıdaki R kod bloğunda basit tekrarsız tesadüfi örnekleme (SRS without replacement) yöntemi kullanılarak veri setindeki gözlemlerin % 70’i eğitilecek veri setine, % 30 ise test edilecek veri setine atanmıştır. Veri setinin eğitilecek veri seti ve test veri setine ayrılmasında genel olarak 70:30 kuralı uygulansa da bu kuralın mutlak olmadığı unutulmamalıdır. Veri setindeki gözlem sayısına göre 70:30 kuralı değişiklik gösterebilmektedir. Veri setindeki gözlem sayısı çok azsa 60:40, veri setindeki gözlem sayısı çok fazla ise 80:20 ve hatta 90:10 olabilmektedir. Şimdi soru burada şu olabilir; neden biz 80:20 veya 90:10 olarak belirliyoruz? Genel olarak buna verilebileceğim cevap şu: Eğer çok yüksek gözlem sayıları ile çalışıyorsanız bilgisayar işlemcisine bağlı olarak bu işlemin çok uzun sürmesi kuvvetle muhtemeldir ki bu durumda test veri setinin oranını düşürmek analizinizi hızlandırır ve daha çabuk sonuç alırsınız.
set.seed(1461)
orneklem<- sample(1:NROW(veri), NROW(veri)*0.7)
train <- veri[orneklem, ]
test <- veri[-orneklem, ]
Torpalama (Bagging) modelinin kurulması
model<-bagging(medv ~ ., data=train, coob=TRUE, nbagg=500)
print(model)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde kurulan modele ait özet çıktı aşağıda verilmiştir.
Bagging regression trees with 500 bootstrap replications
Call: bagging.data.frame(formula = medv ~ ., data = train, coob = TRUE,
nbagg = 500)
Out-of-bag estimate of root mean squared error: 4.3542
Tahmin edilen değerler ile test veri setindeki gözlem değerlerinin karşılaştırılması
model <- bagging(medv ~ ., data=train, coob=TRUE, nbagg=500)
tahmin<-predict(model, test)
karsilastirma<-tibble(Gozlem=test$medv, Tahmin=round(tahmin,1))
#ilk ve son 10 tahmin değerini gözlem değerleriyle karşılaştırma
ilk10<-head(karsilastirma, 10) %>% rename(Gozlemİlk_10=Gozlem, Tahminİlk_10=Tahmin)
son10<-tail(karsilastirma, 10) %>% rename(GozlemSon_10=Gozlem, TahminSon_10=Tahmin)
formattable(cbind("Sıra"=seq(1,10),ilk10, son10))
#karşılaştırmalı sonuçların xlsx dosyasına yazdırılması
write_xlsx(karsilastirma, "karsılastirma_sonuçları.xlsx")
Yukarıdaki R kod bloğunun çalıştırılmasından sonra torbalama (bagging) modelinden elde edilen ilk ve son 10 tahmin değerleri gözlem değerleri ile birlikte aşağıdaki tabloda karşılaştırmalı olarak verilmiştir.
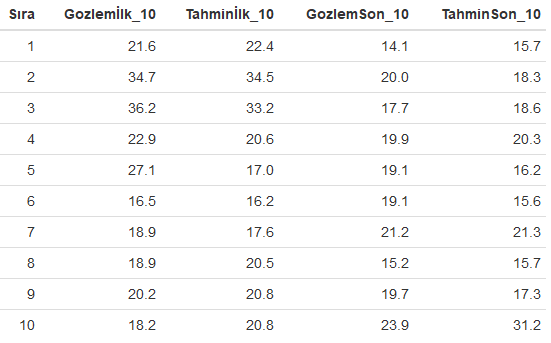
Yukarıdaki R kod bloğunun çalıştırılmasından sonra torbalama (bagging) modelinden elde edilen konut fiyatları tahmin değerleri ile test veri setindeki gözlem değerleri aşağıda xlsx dosyasına yazdırılmıştır. Buradan dosyayı indirerek sonuçları karşılaştırmalı olarak görebilirsiniz.
Tahmin edilen değerler ile test veri setindeki gözlem değerlerinin grafik üzerinde karşılaştırılması
ggplot(karsilastirma, aes(Gozlem, Tahmin)) +
geom_point() +
geom_abline(intercept = 0, slope = 1, size=1.5, color="red")+
ggtitle("Gözlem Değerleri ve Tahmin Edilen Bagging Regresyon Değerleri")+
theme_minimal()
#alternatif grafik
ggplot(karsilastirma, aes(Gozlem, Tahmin)) +
geom_point() +
geom_abline(intercept = 0, slope = 1, color="red", size=1.5)+
ggtitle("Gözlem Değerleri ve Tahmin Edilen Bagging Regresyon Değerleri")+
theme_gray()
Yukarıdaki R kod bloğunun çalıştırılmasından sonra torbalama (bagging) modelinden elde edilen konut fiyatları tahmin değerleri ile test veri setindeki gözlem değerleri aşağıda şekil üzerinde verilmiştir.

Yukarıdaki R kod bloğunun çalıştırılmasından sonra torbalama (bagging) modelinden elde edilen konut fiyatları tahmin değerleri ile test veri setindeki gözlem değerleri aşağıda alternatif olarak şekil üzerinde verilmiştir.

Tahmin edilen değerler ile test veri setindeki gözlem değerlerinin regresyon hata metrikleri açısından değerlendirilmesi
Kurulan modele ait regresyon hata metriklerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.
mse<-MSE(karsilastirma$Gozlem, karsilastirma$Tahmin)
mape<-MAPE(karsilastirma$Gozlem, karsilastirma$Tahmin)
rmse<-RMSE(karsilastirma$Gozlem, karsilastirma$Tahmin)
sse<-sse(karsilastirma$Gozlem, karsilastirma$Tahmin)
mae<-mae(karsilastirma$Gozlem, karsilastirma$Tahmin)
formattable(round(tibble(SSE=sse, MSE=mse, RMSE=rmse, MAE=mae, MAPE=mape),2))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen regresyon hata metrikleri bir bütün olarak aşağıda verilmiştir. Torbalama (bagging) algoritmasıyla kurulan model test veri seti ile karşılaştırıldığında konut fiyatlarını yaklaşık % 2,7 ortalama mutlak hata (MAE) ve yaklaşık % 3,5 kök ortalama kare hatası (RMSE) ile tahmin ettiği görülmektedir.

Performans Testleri
Bu bölümde kurulan model iki yöntemle tüm veri seti üzerinde test edilmiştir. Kullanılan performans test yöntemleri sırasıyla şöyledir:
- Çapraz performans testi (Cross validation test)
- Hold out yöntemi
Çapraz performans testi (Cross validation test)
Burada modelin performansı çapraz performans testi yapılarak tüm veri seti üzerinde test edilir ve hata oranı verilir. Bu işleme ilişkin yazılan R kod bloğu aşağıda verilmiştir.
errorest(medv ~ ., data=veri, model=lm, est.para=control.errorest(random=FALSE))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra model tüm veri seti üzerinde test edilmiş ve performans metriği aşağıda verilmiştir.Torbalama (bagging) algoritmasıyla kurulan model tüm veri seti ile karşılaştırıldığında konut fiyatlarını yaklaşık % 5,88 kök ortalama kare hatası (RMSE) ile tahmin ettiği görülmektedir.
Call:
errorest.data.frame(formula = medv ~ ., data = veri, model = lm,
est.para = control.errorest(random = FALSE))
10-fold cross-validation estimator of root mean squared error
Root mean squared error: 5.877
Hold out yöntemi
Burada modelin performansı Holdout yöntemi ile testi yapılarak tüm veri seti üzerinde test edilir ve hata oranları verilir. Bu işleme ilişkin yazılan R kod bloğu aşağıda verilmiştir.
set.seed(61)
bs<- performanceEstimation(
PredTask(medv ~ ., veri),
workflowVariants(learner="bagging", learner.pars=list(coob=TRUE, nbagg=500)),
EstimationTask(metrics = c("mse","rmse", "mae"),
method = Holdout(nReps=3,hldSz=0.3)))
summary(bs)
plot(bs)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra model tüm veri seti üzerinde test edilmiş ve performans hata metrikleri aşağıda verilmiştir. Bulgular, torbalama algoritmasının tüm veri seti üzerinde test edildiğinde konut fiyatlarını yaklaşık % 2,7 ortalama mutlak hata (MAE) ve yaklaşık % 4,1 kök ortalama kare hatası (RMSE) ile tahmin ettiğini göstermektedir.
##### PERFORMANCE ESTIMATION USING HOLD OUT #####
** PREDICTIVE TASK :: veri.medv
++ MODEL/WORKFLOW :: bagging
Task for estimating mse,rmse,mae using
3 x 70 % / 30 % Holdout
Run with seed = 1234
Iteration : 1 2 3
== Summary of a Hold Out Performance Estimation Experiment ==
Task for estimating mse,rmse,mae using
3 x 70 % / 30 % Holdout
Run with seed = 1234
* Predictive Tasks :: veri.medv
* Workflows :: bagging
-> Task: veri.medv
*Workflow: bagging
mse rmse mae
avg 16.855399 4.0947040 2.6861979
std 3.011187 0.3649621 0.2642337
med 16.443337 4.0550385 2.5892506
iqr 2.989967 0.3633419 0.2505401
min 14.071462 3.7511948 2.4841314
max 20.051396 4.4778786 2.9852116
invalid 0.000000 0.0000000 0.0000000
Yukarıdaki R kod bloğunun çalıştırılmasından sonra model tüm veri seti üzerinde test edilmiş ve performans hata metrikleri aşağıda şekil üzerinde gösterilmiştir.

Sonuç
Bu çalışmada regresyon (regression) probleminin çözümüne yönelik topluluk öğrenme algoritmalarından biri olan torbalama (bagging) algoritması kullanılarak ayrıntılı deneysel bir çalışma yapılmıştır. Ortaya konulan bulgular, regresyon probleminin torbalama (bagging) algoritması ile çok başarılı bir şekilde, diğer bir ifadeyle düşük hata oranlarıyla çözüme kavuşturulduğunu göstermektedir.
Torbalama algoritması test verisi üzerinde test edildiğinde konut fiyatlarını yaklaşık % 2,7 ortalama mutlak hata (MAE) ve yaklaşık % 3,5 kök ortalama kare hatası (RMSE) ile tahmin ettiği görülmektedir. Diğer taraftan kurulan model tüm veri seti üzerinde çapraz performans testi ile test edildiğinde ise konut fiyatlarını yaklaşık % 5,88 kök ortalama kare hatası (RMSE) ile tahmin ediyor iken, kurulan model tüm veri seti üzerinde Hold out yöntemi ile test edildiğinde ise konut fiyatlarını yaklaşık yaklaşık % 2,7 ortalama mutlak hata (MAE) ve yaklaşık % 4,1 kök ortalama kare hatası (RMSE) ile tahmin ettiği görülmektedir.
Yapılan bu çalışmanın özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına önemli bir katkı sunacağı düşünülmektedir.
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
- https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
- http://lib.stat.cmu.edu/datasets/boston
- https://tevfikbulut.com/2020/05/21/r-programlama-diliyle-regresyon-problemlerinin-cozumunde-rastgele-orman-algoritmasi-uzerine-bir-vaka-calismasi-a-case-study-on-random-forest-rf-algorithm-in-solving-regression-problems-with-r-progr/
- https://www.stat.berkeley.edu/~breiman/Using_random_forests_V3.1.pdf
- https://www.stat.berkeley.edu/~breiman/RandomForests/
- https://stats.idre.ucla.edu/r/library/r-library-introduction-to-bootstrapping/
- https://stanford.edu/~shervine/l/tr/teaching/cs-229/cheatsheet-machine-learning-tips-and-tricks
- http://uzalcbs.org/wp-content/uploads/2016/11/2012_082.pdf
- http://www.ub.edu/stat/docencia/EADB/bagging.html
- https://people.cs.pitt.edu/~milos/courses/cs2750-Spring04/lectures/class23.pdf
- https://www.google.com/search?q=underfitting+and+overfitting&source=lnms&tbm=isch&sa=X&ved=2ahUKEwiI1onvyNvpAhVSQMAKHfYyC28Q_AUoAXoECBAQAw&biw=1366&bih=604#imgrc=m5WcPcAqdpCwEM
- Webb G.I. (2011) Overfitting. In: Sammut C., Webb G.I. (eds) Encyclopedia of Machine Learning. Springer, Boston, MA
- https://www.memorial.com.tr/saglik-rehberleri/biyopsi-nedir-ve-nasil-yapilir/
- https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)
- Andriyas, S. and McKee, M. (2013). Recursive partitioning techniques for modeling irrigation behavior. Environmental Modelling & Software, 47, 207–217.
- Chan, J. C. W. and Paelinckx, D. (2008). Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sensing of Environment, 112(6), 2999–3011.
- Chrzanowska, M., Alfaro, E., and Witkowska, D. (2009). The individual borrowers recognition:Single and ensemble trees. Expert Systems with Applications, 36(2), 6409–6414.
- De Bock, K. W., Coussement, K., and Van den Poel, D. (2010). Ensemble classification based on generalized additive models. Computational Statistics & Data Analysis, 54(6), 1535–1546.
- De Bock, K. W. and Van den Poel, D. (2011). An empirical evaluation of rotation-based ensemble classifiers for customer churn prediction. Expert Systems with Applications, 38(10), 12293–12301.
- Fan, Y., Murphy, T.B., William, R. and Watson G. (2009). digeR: GUI tool for analyzing 2D DIGE data. R package version 1.2.
- Garcia-Perez-de-Lema, D., Alfaro-Cortes, E., Manzaneque-Lizano, M. and Banegas-Ochovo, R. (2012). Strategy, competitive factors and performance in small and medium enterprise (SMEs).
- African Journal of Business Management, 6(26), 7714–7726.
- Gonzalez-Rufino, E., Carrion, P., Cernadas, E., Fernandez-Delgado, M. and Dominguez-Petit, R.(2013). Exhaustive comparison of colour texture features and classification methods to discriminate cells categories in histological images of fish ovary. Pattern Recognition, 46, 2391–2407.
- Krempl, G. and Hofer, V. (2008). Partitioner trees: combining boosting and arbitrating. In: Okun, O., Valentini, G. (eds.) Proc. 2nd Workshop Supervised and Unsupervised Ensemble Methods and Their Applications, Patras, Greece, 61–66.
- Torgo, Luis, Data Mining With R. Second Edition.