Rastlantı ya da kesin olmayan olaylarla ilgilenen olasılık teorisi, rastlantı olaylarını belirli kurallara göre matematik disiplininde inceleyen bir bilim dalıdır. Rastlantı olayından kasıt gerçekleşmesi şansa bağlı olan önceden kesin olarak bilinmeyen olaylardır. Burada olabildiğince yalın bir şekilde uygulamalı örneklerin şans oyunları üzerinden verilmesinin nedeni olasılık konusuna dikkat çekmek ve konunun öğrenilmesine katkıda bulunmaktır, yoksa amaç bu oyunları oynamaya özendirmek veya teşvik emek değildir. Bunu burada özellikle ifade etmek gerekir.
Sayısal loto gibi diğer şans oyunları da bir olasılık temeline dayandığı için önceden kesin olarak bilinmeyen olaylardır. Bu yüzden olasılıktan bahsederiz. Oynanan kupon veya kolon sayısı artıkça şansınız, diğer bir ifadeyle kazanma olasılığınız artmaktadır. Örneklem uzayının 49 olduğu sayısal lotodan örnek vermek gerekirse 6’lı kombinasyonu yakalama olasılığınız yaklaşık 14 milyon (13.983.816)’da 1’dir. Diyelim ki 1 milyon kolon sayısal loto oynadınız. Bu durumda sizin kazanma olasılığınız kalan olasılığı dikkate alarak söyler isek 13.983.816-1000000=12983816’da 1’dir. Bu olasılıkları tekrarsız kombinasyonla hesaplamaktayız ( c(49 6)=13.983.816). Temelde sayısal loto kürede yer alan 49 toptan seçilen 6 topun geri koyulmamak şartıyla kalanlar arasında seçilmesi esasına dayanır ki buna biz örneklem biliminde tekrarsız basit tesadüfi örnekleme (simple random sampling without replacement) deriz. Yani 49 toptan her birine eşit seçilme şansı veririz.
Bahsettiğimiz üzere tekrarsız basit tesadüfi örneklemede çekilmiş bir sayı sonraki tüm çekimlerde popülasyondan çıkarıldığından popülasyonda her bir sayı eşit seçilme şansına sahip olur. Bu bağlamda tekrarsız basit tesadüfi örnekleme notasyonunu aşağıdaki gibi yazabiliriz.

Çalışma kapsamında R programlama dili ve bu programlama dilini bilmeyenlerin olabileceği dikkate alınarak Microsoft Office Excel kullanılarak Sayısal Loto ve 01.08.2020 tarihinde yürürlüğe giren Çılgın Sayısal Loto kombinasyonları hesaplanarak kazanma olasılıkları karşılaştırmalı olarak verilmiştir. Çılgın Sayısal Loto’nun gelmesiyle Sayısal Loto’nun uygulamadan kalkmasına rağmen burada ikramiye kazanma olasılıklarının verilmesinin nedeni her iki şans oyunu arasında kazanma olasılıkları açısından karşılaştırma sağlayabilmektir.
Sayısal Loto ve Çılgın Sayısal Loto Eşitliği
Hem Sayısal Loto hem de Çılgın Sayısal Loto’da kazanma olasılıklarının hesaplanmasında aşağıdaki eşitlik kullanılmıştır. Eşitlik aynı zamanda kesikli olasılık dağılımlarından Hipergeometrik Dağılım (Hypergeometric Distribution) olarak adlandırılmaktadır.
- Eşitlikte yer alan x örneklem uzayını göstermektedir. Sayısal Loto’da örneklem uzayı 1’den 49’da kadar (bu sayı dahil) sayılardan oluşmakta iken Çılgın Sayısal Loto’da ise örneklem uzayı 1’den 90’a kadar (bu sayı dahil) sayılardan oluşmaktadır. Sayısal loto örneklem uzayı x ∈ {1,2,3,4,5,…………….,49} iken Çılgın Sayısal Loto’da ise x ∈ {1,2,3,4,5,…………….,90}’dır.
- Eşitlikte yer alan k, 90 veya 49 sayı içerisinden çekilecek top sayısını göstermektedir. k yapılan hesaplamalarda 6 olarak alınmıştır. Bunun nedeni her iki örneklem uzayından da 6 top çekilmiş olmasıdır.
- Eşitlikte yer alan b, eşleşen top sayısını göstermektedir. Kombinasyonda hangi kazanma olasılıklarını hesaplayacaksanız b yerine onu yazmalısınız.

İlk olarak yüklenecek birkaç R kütüphanesini aşağıda verelim.
kütüphaneler = c("dplyr","tibble","tidyr","formattable")
sapply(kütüphaneler, require, character.only = TRUE)
Sayısal Loto ikramiye kazanma olasılıkları
Burada esasında olasılık teorisindeki kombinasyon formülünü kullanarak 49 sayı içerisinden 6, 5, 4 ve 3 çıkma olasılıklarını hesaplayacağız. Bu amaçla yazılan R kod bloğuna aşağıda yer verilmiştir. R’da choose () fonksiyonu kombinasyon hesaplamalarında kullanılmaktadır.
formattable(tibble("Altılı"= choose(49, 6)/(choose(6, 6)*choose(43, 0)), "Beşli"= choose(49, 6)/(choose(6, 5)*choose(43, 1)), "Dörtlü"= choose(49, 6)/(choose(6, 4)*choose(43, 2)), "Üçlü"= choose(49, 6)/(choose(6, 3)*choose(43, 3))))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen sayısal loto ikramiye olasılıkları kombinasyonlara göre aşağıdaki tabloda verilmiştir. Ortaya konulan bulgulara göre 49 sayı içerisinde;
- 6 bilme şansınız 13.983.816’da 1’dir.
- 5 bilme şansınız 54.200,8’de 1’dir.
- 4 bilme şansınız 1.032,4’te 1’dir.
- 3 bilme şansınız 56,6’da 1’dir.

Çılgın Sayısal Loto ikramiye kazanma olasılıkları
Burada ise sayısal lotoda olduğu gibi olasılık teorisindeki kombinasyon formülünü kullanarak 90 sayı içerisinden 6, 5, 4, 3 ve 2 kazanma olasılıklarını hesaplayacağız. Bu amaçla yazılan R kod bloğuna aşağıda yer verilmiştir.
formattable(tibble("Altılı"= choose(90, 6)/(choose(6, 6)*choose(84, 0)), "Beşli"= choose(90, 6)/(choose(6, 5)*choose(84, 1)), "Dörtlü"= choose(90, 6)/(choose(6, 4)*choose(84, 2)), "Üçlü"= choose(90, 6)/(choose(6, 3)*choose(84, 3)), "İkili"= choose(90, 6)/(choose(6, 2)*choose(84, 4))))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen sayısal loto ikramiye olasılıkları kombinasyonlara göre aşağıdaki tabloda verilmiştir. Ortaya konulan bulgulara göre 90 sayı içerisinde;
- 6 bilme şansınız 622.614.630’da 1’dir.
- 5 bilme şansınız 1.235.346’da 1’dir.
- 4 bilme şansınız 11.906,95’te 1’dir.
- 3 bilme şansınız 326,72’de 1’dir.
- 2 bilme şansınız 21,51’te 1’dir.

Sayısal Loto ve Çılgın Sayısal Loto Kazanma Olasılıklarını Karşılaştırma
- İlk olarak 6’lı kombinasyonu tutturma olasılıklarını ele alacak olursak Çılgın Sayısal Loto’da 6 bilme şansınız Sayısal Loto’ya göre 44,52 kat daha düşüktür (622.614.630 / 13.983.816 = 44,52).
- 5’li kombinasyonu tutturma olasılıklarını ele alacak olursak Çılgın Sayısal Loto’da 5 bilme şansınız Sayısal Loto’ya göre yaklaşık 22. 8 kat daha düşüktür (1.235.346 / 54.200,8 = 22,79).
- 3’lü kombinasyonu tutturma olasılıklarını ele alacak olursak Çılgın Sayısal Loto’da 4 bilme şansınız Sayısal Loto’ya göre yaklaşık 11,5 kat daha düşüktür (11.906,95 / 1.032,4 = 11,53).
- 3’lü kombinasyonu tutturma olasılıklarını ele alacak olursak Çılgın Sayısal Loto’da 3 bilme şansınız Sayısal Loto’ya göre yaklaşık 5,77 kat daha düşüktür (326,72 / 56,6 = 5,77).
R programlama bilmeyenlerin için de aynı uygulamalar Microsoft Office Excel ortamında yapılarak daha kalıcı olması amaçlanmıştır. Excel’de kombinasyon hesaplamaları =KOMBİNASYON() fonksiyonu ile yapılmıştır. Sayısal Loto örneği üzerinden gidilerek 6’lı kombinasyonu tutturma olasılığı excelde aşağıda formül kombinasyonları ile hesaplanmıştır. Diğer olasılıklar da aynı formül kombinasyonları ile Çılgın Sayısal Loto için de hesaplanmıştır. Burada yapılan tek şey yukarıda verilen eşitliğin excele taşınmasıdır.
=KOMBİNASYON(49;6)/(KOMBİNASYON(6;6)*KOMBİNASYON(49-6;6-6))
Excel üzerinde yapılan uygulamaları sırasıyla tablolar halinde verelim.

Şimdi de Çılgın Sayısal Loto kazanma şanslarının Sayısal Loto’ya göre ne kadar olduğunu aşağıdaki tabloda karşılaştırmalı olarak ortaya koyalım.

Excel üzerinde yaptığım bu uygulamaları kullanılan fonksiyonları da görebilmeniz adına aşağıda xlsx uzantılı olarak paylaşıyorum.
Ayrıca R’da Çılgın Sayısal Loto ve Sayısal Loto olasılıklarını birlikte görebilmeniz adına aşağıda yazdığım kod bloğunda hesaplanmıştır.
options(scipen=999)#bilimsel notasyondan sonuçları kurtarmak için
N=90#Anakütledeki eleman sayısı (N) 90'dir.
n=6#Örneklem hacmi (n) 6'dır.
m=6#Popülasyondaki başarı sayısı (m) 6'dır.
x=2:6#Örneklemdeki başarı sayısı (x) 2'den 6'ya kadar (dahil)
N1=49#Anakütledeki eleman sayısı (N) 49'dur: sayısal loto için
x1=3:6#Örneklemdeki başarı sayısı (x) 3'den 6'ya kadar (dahil):sayısal loto için
#çılgın sayısal loto tablosu
olasilik<-choose(m,x)*choose(N-m,n-x)/choose(N,n)
olasilik<-olasilik %>% as_tibble() %>% rename(Cilgin_Olasilik=value) %>% mutate_if(is.numeric, round,10) %>% add_column("Kategori"=x, .before="Cilgin_Olasilik") %>% mutate(CilginCT=round(1/olasilik,2)) %>% arrange((Cilgin_Olasilik))
#sayısal loto tablosu
olasilik1<-choose(m,x1)*choose(N1-m,n-x1)/choose(N1,n)
olasilik1<-olasilik1 %>% as_tibble() %>% rename(Sayisal_Olasilik=value) %>% mutate_if(is.numeric, round,10) %>% mutate(SayısalCT=round(1/olasilik1,2)) %>% arrange((Sayisal_Olasilik)) %>% add_row(tibble(Sayisal_Olasilik = 0, "SayısalCT" = 0))
#tabloların birleştirilmesi
cbind(olasilik, olasilik1)%>% as_tibble() %>% mutate(Sayisal_Olasilik = replace(Sayisal_Olasilik, Sayisal_Olasilik == 0, "")) %>% mutate(SayısalCT = replace(SayısalCT, SayısalCT == 0, "")) %>% formattable()
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen olasılık değerleri, daha kolay anlaşılması adına çarpmaya göre tersi (Tabloda CT olarak kısaltılmıştır.) de alınarak aşağıdaki tabloda verilmiştir.
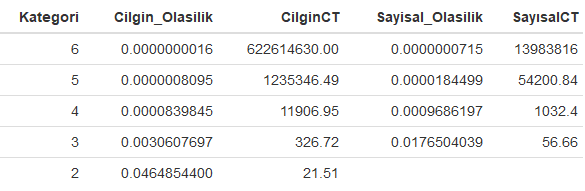
Ortaya konulan araştırma bulguları Çılgın Sayısal Loto kazanma olasılıklarının Sayısal Loto kazanma olasılıklarından çok daha düşük olduğunu göstermektedir.
Özetle R’da ve Microsoft Excel’de yapılan bu özgün çalışmayla olasılık teorisinde yer alan kombinasyon fonksiyonları kullanılarak şans oyunları özelinde olasılık teorisine dikkat çekilmeye çalışılmıştır.
Şans oyunlarındaki olasılık hesaplarının temelini oluşturan Hipergeometrik olasılık dağılımı ile ilgili olarak daha detaylı bilgi almak için aşağıdaki linkte yer alan çalışmamdan yararlanabilirsiniz.
Hipergeometrik Olasılık Dağılımı Üzerine Bir Vaka Çalışması
Yukarıda yapılan işlemler R programlama dili kullanarak geliştirdiğim shiny web uygulaması üzerinde de hesaplanabilir. Linkleri aşağıda paylaşıyorum.
Hipergeometrik Olasılık Hesaplayıcı. 01.09.2020. https://buluttevfik.shinyapps.io/HypergeometricProbabilityCalculator/
Hipergeometrik Olasılık Hesaplayıcı. Versiyon 1. 15.09.2020. Uygulamanın linki: https://buluttevfik.shinyapps.io/Hipergeometrikolasilikhesaplayiciv1/
Ayrıca yukarıda örnek uygulaması yapılan vaka çalışması Pyhon programlama dili bilenler için Python üzerinde de tarafımdan uygulamalı olarak gösterilmiştir. Bu çalışmada farklı olarak Çılgın Sayısal Loto’da 5+1 kazanma olasılığı da hesaplanmıştır. Çalışmanın linki aşağıdadır.
Python’da Şans Oyunları Perspektifinden Olasılık
Olasılık perspektifinden diğer şans oyunlarının da uygulamalı olarak değenlendirildiği çalışmaların linkleri de ilgilenenler için aşağıda verilmiştir.
Şans Oyunları Perspektifinden Olasılık II: Probability from Perspective of the Chance Games II
Şans Oyunları Perspektifinden Olasılık III: Probability from Perspective of the Chance Games III
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla.
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
- https://tevfikbulut.com/2020/08/30/hipergeometrik-olasilik-dagilimi-uzerine-bir-vaka-calismasi-a-case-study-on-hypergeometric-probability-distribution/
- https://tevfikbulut.com/2020/07/26/bernoulli-dagilimi-uzerine-bir-vaka-calismasi-a-case-study-on-the-bernoulli-distribution/
- The R Project for Statistical Computing. https://www.r-project.org/
- https://en.wikipedia.org/wiki/Lottery_mathematics#Choosing_6_from_49
- Microsoft Office Excel 2016 Versiyonu, Microsoft Corporation.
- Hipergeometrik Olasılık Hesaplayıcı. 01.09.2020. https://buluttevfik.shinyapps.io/HypergeometricProbabilityCalculator/
- Hipergeometrik Olasılık Hesaplayıcı. Versiyon 1. 15.09.2020. Uygulamanın linki: https://buluttevfik.shinyapps.io/Hipergeometrikolasilikhesaplayiciv1/