R Programlama Diliyle Sınıflandırma Problemlerinin Çözümünde Rastgele Orman Algoritması Üzerine Bir Vaka Çalışması: A Case Study on Random Forest (RF) Algorithm in Solving Classification Problems with R Programming Language

Giriş

Rastgele Orman (RF) algoritması , 2001 yılında Breiman tarafından karar ağaçlarının bir kombinasyonu olarak önerilmiştir. RF en iyi “her ağaç, bağımsız olarak örneklenen ve ormandaki tüm ağaçlar için aynı dağılıma sahip rastgele bir vektörün değerlerine bağlı olacak şekilde ağaç belirleyicilerinin kombinasyonu” olarak tanımlanan bir topluluk makine öğrenme algoritmasıdır. Topluluk algoritması gerek regresyon gerekse sınılandırma problemlerinde varyansı ve hatayı azaltarak daha iyi hedef değişken veya bağımlı değişkeni tahmin etmemize olanak tanır. Bunu da yeniden örnekleme yöntemi (bootstrap aggregation or bagging)’yle yapar. Bu yöntemde sırasıyla tesadüfi tekrarlı örneklem yöntemi (simple random sampling with replacement) kullanılarak veri seti alt örneklem kümelerine, diğer bir ifade ile alt örneklem ağaç kümelerine ayrılır. Bunların tamamı kurulan modelde hatayı azaltmaya yöneliktir. Anlatılanı Şekil 1 üzerinde gösterelim. Şekilde modellerin paralel düzende inşa edildiğine dikkat etmek gerekir. Modellerin oluşturulmasında çaprazlama bulunmamaktadır.

Şekil 1: Rastgele Orman Algoritmasında Yeniden Örnekleme (Bootstrapping)

RF, karar ağaçlarına dayanır. Makine öğreniminde karar ağaçları, tahmin modelleri oluşturan denetimli öğrenme tekniğidir. Bunlara karar ağaçları (decision trees) adı verilmektedir. Bu yöntemin özellikle mühendislik bilimlerinde başta sağlık sektörü olmak üzere pek çok sektörde yaygın bir şekilde kullanıldığı görülmektedir.

Rastgele orman algoritmaları hem sınıflandırma (classification) hem de regresyon (regression) problemlerinin çözümünde kullanılan makine öğrenmenin denetimli öğrenme (supervised) kısmında yer alan tahmin oranı yüksek algoritmalardır. Burada aslında sınıflandırma ve regresyondan kasıt tahmin edilecek bağımlı veya hedef değişkenin veri tipi ifade edilmektedir. Sınıflandırma ve regresyon için kullanılan veri tipleri Şekil 2’de sunulmuştur. Cevap değişkeni ya da bağımlı değişken kategorik ise rastgele orman algoritmasında sınıflandırma, bağımlı değişken nicel ise rastgele orman algoritmasında regresyon problemini çözmüş oluyoruz. RF analizlerde uç değerler (outliers)’e duyarlı değildir.

Şekil 2: Rastgele Orman (RF) Algoritmasında Proplem Sınıfına Göre Veri Tüleri

RF’te kurulan modelin veya modellerin performansını değerlendirmede kullanılan hata metrikleri ise genel itibariyle Şekil 3’te verilmiştir. Şekil 3’te yer verilen hata metrikleri gerek makine öğrenme gerekse derin öğrenme modellerinin performansının testinde sıklıkla kullanılmaktadır.

Şekil 3: Rastgele Orman Algoritması Hata Metrikleri

Şekil 3’te sınıflandırma problemlerinin çözümünde kullanılan hata metriklerini şimdi de ele alalım. Karışıklık matrisi (confusion matrix) olarak olarak adlandırılan bu matris sınıflandırma problemlerinin çözümünde hata metriklerini ortaya koyarak kurulan modelin veya modellerin hata oranını değerlendirmektedir. Hata matrisinin makine ve derin öğrenme metotlarının değerlendirilmesinde sıklıkla kullanıldığı görülmektedir. Aşağıda yer alan tabloda hata metriklerinin hesaplanmasına esas teşkil eden tablo verilmiştir. Bu tabloyla sınıflandırma hataları hesaplanabilmektedir. Tabloda yer verilen Tip 1 hata (Type 1 error) istatistikte alfa hatasını göstermektedir. Tip 1 hata H0 hipotezi (null hpypothesis) doğru olduğu halde reddedilmesidir. Tabloda Tip 2 hata (Type II error) olarak adlandırılan hata ise istatistikte Beta hatası olarak da bilinmektedir. Tip 2 hata ise H0 hipotezi (null hpypothesis) yanlış olduğu halde kabul edilmesidir.

Şekil 3’te de yer verildiği üzere literatürde sınıflandırma modellerinin performansını değerlendirmede aşağıdaki metriklerden yaygın bir şekilde yararlanıldığı görülmektedir.

• Doğruluk (Accuracy): TP+TN / TP+TN+FP+FN eşitliği ile hesaplanır. Modelin genel performansını ortaya koyar. Bu sınıflandırma metriği ile aslında biz informal bir şekilde dile getirirsek doğru tahminlerin toplam tahminler içindeki oranını hesaplamış oluyoruz.
• Kesinlik (Precision): TP / TP+FP eşitliği ile hesaplanır. Doğru tahminlerin ne kadar kesin olduğunu gösterir.
• Geri çağırma (Recall): TP / TP+FN eşitliği ile hesaplanır. Gerçek pozitif örneklerin oranını verir.
• Özgünlük (Specificity): TN / TN+FP eşitliği ile hesaplanır. Gerçek negatif örneklerin oranını gösterir.
• F1 skoru : 2TP / 2TP+FP+FN eşitliği ile hesaplanır. Dengesiz sınıflar için yararlı hibrit bir metrik olup, kesinlik (precision) ve geri çağırma (recall) skorlarının ağırlıklı ortalamasını ifade etmektedir.
• ROC (Receiver operating characteristic): Yukarıda karışıklık matrisinde belirtilen parametrelerden yararlanılarak hesaplanır. ROC eğrisi olarak da adlandırılmaktadır. ROC eğrileri, herhangi bir tahmin modelinin doğru pozitifler (TP) ve negatifler (TN) arasında nasıl ayrım yapabileceğini görmenin güzel bir yoludur. Sınıflandırma modellerin perfomansını eşik değerler üzerinden hesaplar. ROC iki parametre üzerinden hesaplanır. Doğru Pozitiflerin Oranı (TPR) ve Yanlış Pozitiflerin Oranı (FPR) bu iki parametreyi ifade eder. Burada aslında biz TPR ile Geri Çağırma (Recall), FPR ile ise 1-Özgünlük (Specificity)‘ü belirtiyoruz.
• Cohen Kappa: Kategorik cevap seçenekleri arasındaki tutarlılığı ve uyumu gösterir. Cohen, Kappa sonucunun şu şekilde yorumlanmasını önermiştir: ≤ 0 değeri uyumun olmadığını, 0,01–0,20 çok az uyumu, 0,21-0,40 az uyumu, 0,41-0,60 orta, 0,61-0,80 iyi uyumu ve 0,81–1,00 çok iyi uyumu göstermektedir. 1 değeri ise mükemmel uyum anlamına gelmektedir.

Metodoloji ve Uygulama Sonuçları

Bu kısımda kullanılan veri setine ve adım adım Rastgele Orman algoritması uygulamasına yer verilmiştir. Analizde R programlama dili kullanılmıştır. Uygulamaya esas veri seti “https://archive.ics.uci.edu/ml/machine-learning-databases/car/” veri tabanından alınmıştır. Veri seti araba seçimi yapan bireylerin cevaplarından oluşmaktadır. Orjinal (ingilizce) veri setini aşağıdaki linkten indirebilirsiniz.

R’da analize uygun hale getirdiğim aynı veri setinin Türkçe versiyonunu ise aşağıdaki linkten indirebilirsiniz. Veri setinin Türkçeye çevrilmesinin nedeni anlaşılırlığın artırılmak istenmesidir.

Veri seti ID (Sıra) hariç 7 değişkenden oluşmakta olup, anlaşılırlığı artırmak adına Türkçeye çevrilerek yeniden kodlanmıştır. Değişkenlerin tamamının veri türü kategorik olup değişkenler sırasıyla şöyledir:

1. Fiyat: Araba fiyatlarını belirtmekte olup , “Düşük”, “Orta”, “Yüksek” ve “Çok Yüksek” cevap seviyelerinden oluşmaktadır.
2. Bakım: Araba bakımını belirtmekte olup , “Düşük”, “Orta”, “Yüksek” ve “Çok Yüksek” cevap seviyelerinden oluşmaktadır.
3. Kapı: Arabadaki kapı sayısını belirtmekte olup “5 ve Yukarı”, “2”, “3” ve “4” cevap seviyelerinden oluşmaktadır.
4. Kişi: Arabanın kaç kişilik olduğunu göstermekte olup “5 ve Yukarı”, “2” ve “4” cevap seviyelerinden oluşmaktadır.
5. Bagaj: Arabadaki bagaj hacmini değerlendirmeye yönelik “Büyük”, “Orta” ve “Küçük” cevap seviyelerinden oluşmaktadır.
6. Güvenlik: Arabanın oluşturduğu güvenlik algısını değerlendirmeye yönelik “Yüksek”, “Orta” ve “Düşük” cevap seviyelerinden oluşmaktadır.
7. Karar: Araba satın alma durumunu değerlendirmeye yönelik “Kabul”, “İyi”, “Red” ve “Çok İyi” cevap seviyelerinden oluşmaktadır.

Metodoloji ve uygulama sonuçları başlığı altında Rastgele Orman algoritmasına üzerine kurulan iki model olabilecek en yalın şekilde ele alınmaya çalışılmıştır. Daha sonra kurulan bu iki model hata metrikleri açısından performansları karşılaştırılmıştır. Analize başlamadan önce analiz için yüklenecek R kütüphaneleri verelim. Ardından keşifsel veri analizi (EDA) ile veri setini tanıyalım.

Yüklenecek kütüphaneler

kütüphaneler = c("dplyr","tibble","tidyr","ggplot2","formattable","readr","readxl","xlsx", "pastecs","randomForest", "aod", "DescTools", "readstata13","viridis","ggpurr","writexl","ggfortify", "caret", "yardstick","MASS")
sapply(kütüphaneler, require, character.only = TRUE)

Veri setinin okunması ve değişken kategorilerinin yeniden kodlanması

df <- read.csv("car.data", header=FALSE) %>% as_tibble()
df <- df %>% rename(Fiyat=V1, Bakim=V2, Kapi=V3, Kisi=V4, Bagaj=V5, Guvenlik=V6, Karar=V7) %>% rowid_to_column() %>% rename(ID=rowid)
df
df1<-df %>% mutate(Fiyat=recode_factor(Fiyat, "low"="Düşük", "med"="Orta", "high"="Yüksek", "vhigh"="Çok Yüksek"))%>% mutate(Bakim=recode_factor(Bakim, "low"="Düşük", "med"="Orta", "high"="Yüksek", "vhigh"="Çok Yüksek")) %>% mutate (Kapi= recode_factor(Kapi, "5more" = "5 ve Yukarı")) %>% mutate (Kisi= recode_factor(Kisi, "more" = "5 ve Yukarı")) %>% mutate (Bagaj= recode_factor(Bagaj, "big" = "Büyük", "med" = "Orta", "small" = "Küçük")) %>% mutate (Guvenlik= recode_factor(Guvenlik, "high" = "Yüksek", "med" = "Orta", "low" = "Düşük"))%>% mutate (Karar= recode_factor(Karar, "acc" = "Kabul", "good" = "İyi", "unacc" = "Red","vgood" = "Çok İyi"))
df1
formattable(head(df1))

Veri setinin xlsx dosyasına yazdırılması

İhtiyaç duymanız halinde fonksiyonu ile birlikte yeniden kodlanan veri seti aşağıdaki kod yardımıyla xlsx uzantılı olarak excel dosyasına yazdırılmıştır.

write_xlsx(df1, "veriseti.xlsx")

Yukarıdaki R kod bloğunun çalıştırılması ile edilen veri seti dosyası xlsx uzantılı olarak aşağıda verilmiştir.

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen veri setinin ilk 6 satırı aşağıda verilmiştir.

Veri setindeki değişkenlerin özellikleri

str(df1)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra veri setindeki değişkenlerin veri tipi ve faktör (kategori) seviyeleri aşağıda verilmiştir.

Classes ‘tbl_df’, ‘tbl’ and 'data.frame':	1728 obs. of  8 variables:
 $ ID      : int  1 2 3 4 5 6 7 8 9 10 ...
 $ Fiyat   : Factor w/ 4 levels "Düşük","Orta",..: 4 4 4 4 4 4 4 4 4 4 ...
 $ Bakim   : Factor w/ 4 levels "Düşük","Orta",..: 4 4 4 4 4 4 4 4 4 4 ...
 $ Kapi    : Factor w/ 4 levels "5 ve Yukarı",..: 2 2 2 2 2 2 2 2 2 2 ...
 $ Kisi    : Factor w/ 3 levels "5 ve Yukarı",..: 2 2 2 2 2 2 2 2 2 3 ...
 $ Bagaj   : Factor w/ 3 levels "Büyük","Orta",..: 3 3 3 2 2 2 1 1 1 3 ...
 $ Guvenlik: Factor w/ 3 levels "Yüksek","Orta",..: 3 2 1 3 2 1 3 2 1 3 ...
 $ Karar   : Factor w/ 4 levels "Kabul","İyi",..: 3 3 3 3 3 3 3 3 3 3 ...

Veri setindeki eksik gözlemlerin tespiti

sapply(df1, function(x) sum(is.na(x)))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen çıktı aşağıda verilmiştir.

 ID    Fiyat    Bakim     Kapi     Kisi    Bagaj Guvenlik    Karar 
  0        0        0        0        0        0        0        0 

Değişkenler arasındaki korelasyon

Kategorik değişkenlerin korelasyon katsayılarını hesaplamak için yazılan R kod bloğu aşağıdadır. Değişkenler arasındaki korelasyonu hesaplamak için Kikare testi kullanılmıştır. Bunun nedeni korelasyon katsayısı hesaplanacak her iki değişkenin de nitel ve nominal olmasından kaynaklanmaktadır. Korelasyon katsayısı hesaplanacak değişkenlerden biri ordinal (sıralı) olsaydı bu durumda Spearman korelasyon (SpearmanRho) katsayısının hesaplanması gerekecekti. Diğer taraftan, eğer her iki değişken nicel (sürekli ve kesikli) olsaydı bu durumda Pearson korelasyon katsayısını hesaplayacaktık.

p<-data.frame(lapply(df1[,-c(1,8)], function(x) chisq.test(table(x,df1$Karar), simulate.p.value = TRUE)$p.value))
pvalue<-p %>% as_tibble() %>% pivot_longer(cols = Fiyat:Guvenlik, names_to="Degisken", values_to = "p") %>% mutate(Sonuc=ifelse(p<0.05,"Anlamlı", "Anlamlı Değil")) %>% mutate_if(is.numeric, round, 4)
chi<-data.frame(lapply(df1[,-c(1,8)], function(x) chisq.test(table(x,df1$Karar), simulate.p.value = TRUE)$statistic))
chivalue<-chi %>% as_tibble() %>% pivot_longer(cols = Fiyat:Guvenlik, names_to="Degisken", values_to = "Kikare Test İstatistiği")%>% mutate_if(is.numeric, round, 2)
formattable(cbind(chivalue, pvalue[,-1]))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen korelasyon katsayıları aşağıdaki tabloda verilmiştir.

Veri setinin eğitilecek ve test setine ayrılması

set.seed(1)
#Eğitilecek veri seti (training set)
train1 <- df1 %>% sample_frac(.70)
train1
#Test edilecek veri seti
test1  <- anti_join(df1, train1, by = 'ID')#Anti join fonksiyonu eşleşmeyen kayıtları yani geri kalan kayıtları getirir ve onları test setine atar.
test1

Model 1

1 nolu modelin oluşturulması

model1<-randomForest(Karar ~ ., train1[,-1])
model1
summary(model1)
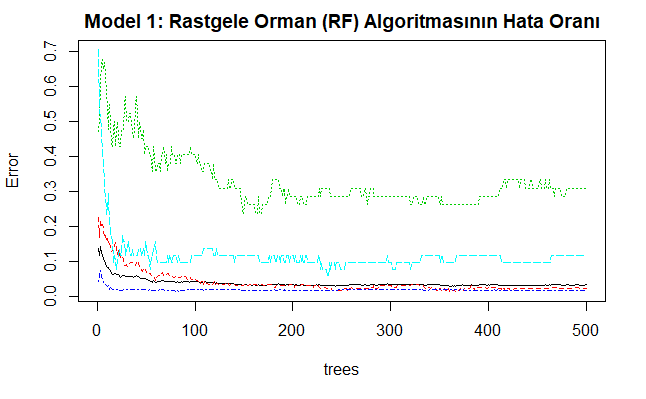
plot(model1, main="Model 1: Rastgele Orman (RF) Algoritmasının Hata Oranı")

Yukarıdaki kod bloğunun oluşturulmasından sonra çizilen 1 nolu modelin grafiği aşağıda verilmiştir. Bu grafik rastgele orman modelinin sınıf hata oranlarını göstermektedir. Ağaç sayısı arttıkça hata oranı sıfıra yaklaşır.

1 nolu modeldeki değişkenlerin önem düzeyleri

k<-importance(model1)
k<-tibble(Değişken=as.vector(row.names(k)), Ortalama_Gini_Katsayısı=as.vector(importance(model1)))%>%arrange(desc(Ortalama_Gini_Katsayısı))
formattable(k)
ggplot(k, aes(x=Ortalama_Gini_Katsayısı, y = Değişken, label=round(Ortalama_Gini_Katsayısı,2)))+
   geom_point()+
    xlab("Ortalama Gini Katsayısı")+
    ylab("Değişken")+
    geom_text(vjust = 0, nudge_y = 0.1)+
    theme_hc()

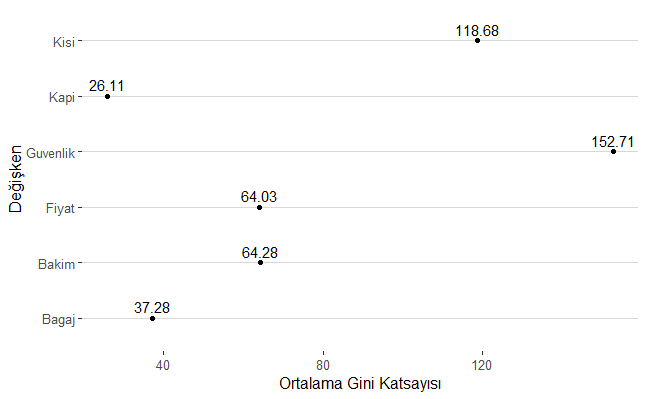
Yukarı kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeyleri ortalama gini katsayısına göre büyükten küçüğe doğru aşağıdaki tabloda verilmiştir.

Yukarı kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeylerine ilişkin grafik ise aşağıda verilmiştir.

Tahmin edilen değerler ile gözlem değerlerinin karşılaştırılması

pred1<-predict(model1, test1)
karsilastirma<-tibble(Gercek=test1$Karar, Tahmin=pred1)
#ilk ve son 10 tahmin değerini gerçek değerle karşılaştırma 
ilk10<-head(karsilastirma, 10) %>% rename(Gercekİlk_10=Gercek, Tahminİlk_10=Tahmin)
son10<-tail(karsilastirma, 10) %>% rename(GercekSon_10=Gercek, TahminSon_10=Tahmin)
formattable(cbind(Id=seq(1,10),ilk10, son10))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modelden elde edilen ilk ve son 10 sınıflandırma değerleri gerçekleşen sınıflandırma değerleri ile birlikte aşağıdaki tabloda karşılaştırmalı olarak verilmiştir.

Karışıklık matrisi (confusion matrix)’nin oluşturulması

pred1<-predict(model1, test1)
karsilastirma<-tibble(Gercek=test1$Karar, Tahmin=pred1)
#alternatif cm ve grafik
cm <- karsilastirma %>%
  conf_mat(Gercek, Tahmin)
cm
autoplot(cm, type = "heatmap")

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisi aşağıda verilmiştir.

     Truth
Prediction Kabul İyi Red Çok İyi
   Kabul     118   1   4       1
   İyi         1  22   2       0
   Red         7   0 345       0
   Çok İyi     0   4   0      13

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisinin grafiği ise aşağıda verilmiştir.

Hata parametreleri

Kurulan 1 nolu modele ait hata parametrelerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.

cm<-confusionMatrix(karsilastirma$Tahmin, karsilastirma$Gercek)
cm

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait hata parametre değerleri aşağıda verilmiştir.

Confusion Matrix and Statistics
          Reference
Prediction Kabul İyi Red Çok İyi
   Kabul     118   1   4       1
   İyi         1  22   2       0
   Red         7   0 345       0
   Çok İyi     0   4   0      13
Overall Statistics
                                         
               Accuracy : 0.9614         
                 95% CI : (0.941, 0.9763)
    No Information Rate : 0.6776         
    P-Value [Acc > NIR] : < 2.2e-16      
                                         
                  Kappa : 0.9192         
                                         
 Mcnemar's Test P-Value : NA             
Statistics by Class:
                     Class: Kabul Class: İyi Class: Red Class: Çok İyi
Sensitivity                0.9365    0.81481     0.9829        0.92857
Specificity                0.9847    0.99389     0.9581        0.99206
Pos Pred Value             0.9516    0.88000     0.9801        0.76471
Neg Pred Value             0.9797    0.98986     0.9639        0.99800
Prevalence                 0.2432    0.05212     0.6776        0.02703
Detection Rate             0.2278    0.04247     0.6660        0.02510
Detection Prevalence       0.2394    0.04826     0.6795        0.03282
Balanced Accuracy          0.9606    0.90435     0.9705        0.96032

Bağımlı değişken kategorilerine göre sınıflandırma metrikleri

class<-cm$byClass#sınıfa göre hata oranları
class<-class %>% as_tibble(class) %>% add_column(Class = c("Kabul", "İyi", "Red", "Çok İyi"), .before = "Sensitivity")
class
class1<-class[, c(1, 2,3,6, 7, 8)]
pivot<-class1 %>% pivot_longer(-Class, names_to = "Parameters", values_to = "Değer")
ggplot(pivot, aes(x="", y = Değer, fill = Class))+
geom_bar(position="stack", stat="identity")+
scale_fill_viridis(discrete = T, option = "E")+
facet_grid(Class~  Parameters)+
xlab("")+
labs(fill = "Kategori")

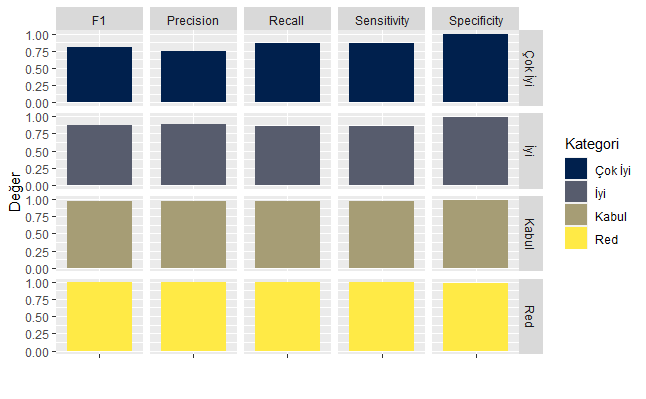
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen bağımlı değişken kategorilerine göre sınıflandırma metrikleri aşağıdaki grafikte verilmiştir.

Çapraz performans testi (Cross validation test)

set.seed(124)
cv<- performanceEstimation(
  PredTask(Karar ~ ., df1[,-1]),
    workflowVariants(learner=("randomForest")),
 EstimationTask(metrics = c("acc","err"),
                method = CV(nReps = 1, nFolds = 10)))
summary(cv)
plot(cv)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

== Summary of a  Cross Validation Performance Estimation Experiment ==
Task for estimating  acc,err  using
 1 x 10 - Fold Cross Validation
	 Run with seed =  1234 
* Predictive Tasks ::  df1[, -1].Karar
* Workflows  ::  randomForest 
-> Task:  df1[, -1].Karar
  *Workflow: randomForest 
               acc         err
avg     0.96860465 0.031395349
std     0.01980161 0.019801612
med     0.96802326 0.031976744
iqr     0.03052326 0.030523256
min     0.94186047 0.005813953
max     0.99418605 0.058139535
invalid 0.00000000 0.000000000

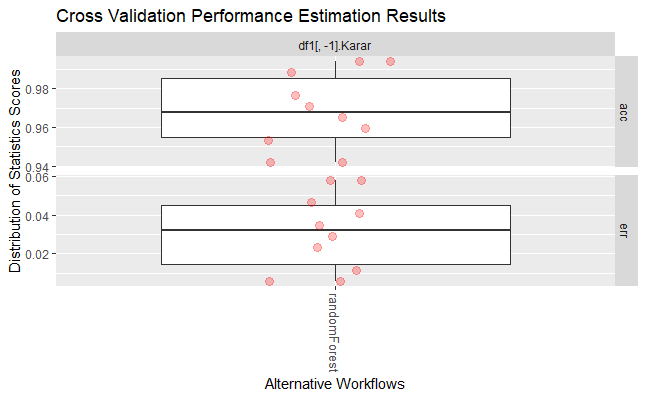
Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıdaki grafikte verilmiştir.

Yeniden örnekleme (bootstrapping) perfomans kontrolü testi

set.seed(1200)
bootstrap <- performanceEstimation(
  PredTask(Karar ~ ., df1[,-1]),
    workflowVariants(learner=("randomForest")),
  EstimationTask(metrics=c("err", "acc"),method=Bootstrap(nReps=100)))
summary(bootstrap)
topPerformers(bootstrap)
plot(bootstrap)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

== Summary of a  Bootstrap Performance Estimation Experiment ==
Task for estimating  err,acc  using
100  repetitions of  e0  Bootstrap experiment
	 Run with seed =  1234 
* Predictive Tasks ::  df1[, -1].Karar
* Workflows  ::  randomForest 
-> Task:  df1[, -1].Karar
  *Workflow: randomForest 
                err         acc
avg     0.039839321 0.960160679
std     0.008783018 0.008783018
med     0.039563417 0.960436583
iqr     0.010807524 0.010807524
min     0.020408163 0.938871473
max     0.061128527 0.979591837
invalid 0.000000000 0.000000000

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

Model 2

2 nolu modelin oluşturulması

2 nolu modelde randomForest() içerisinde ntree parametresi büyütülecek ağaç sayısını göstermektedir. Yazılmadığında otomatik (default) olarak 500 alınmaktadır. Bu sayı çok küçük bir sayıya ayarlanmamalıdır. Ağaç sayısı artıkça kurulan modelde hata oranı azalmaktadır. Fonksiyon içerisinde yer verilen mtyr parametresi ise her bir alt bölünmede tesadüfi bir şekilde örneklenen değişkenlerin sayısını göstermektedir. Fonksiyon içerisinde yer verilen importance parametresi ise değerlendirilecek değişkenlerin önem düzeyini göstermektedir.

model2 <- randomForest(Karar ~ ., train1[,-1], ntree = 500, mtry = 6, importance = TRUE)
model2
summary(model2)
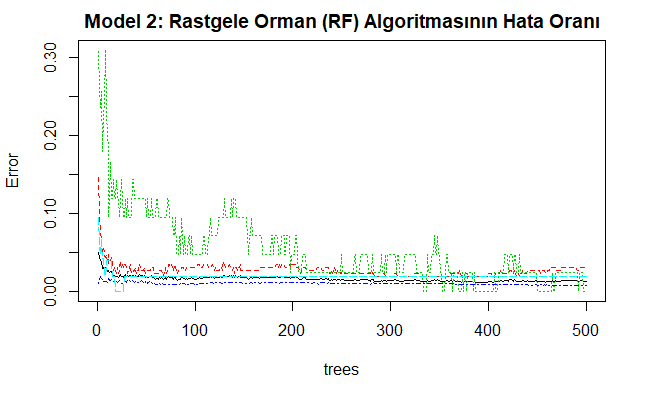
plot(model2, main="Model 1: Rastgele Orman (RF) Algoritmasının Hata Oranı")

Yukarıdaki kod bloğunun oluşturulmasından sonra kurulan 2 nolu modele ait sınılandırma ve hata oranı aşağıda verilmiştir.

Call:
 randomForest(formula = Karar ~ ., data = train1[, -1], ntree = 500,      mtry = 6, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 6
        OOB estimate of  error rate: 1.32%
Confusion matrix:
        Kabul İyi Red Çok İyi class.error
Kabul     250   4   2       2  0.03100775
İyi         0  42   0       0  0.00000000
Red         6   1 852       0  0.00814901
Çok İyi     1   0   0      50  0.01960784

Yukarıdaki kod bloğunun oluşturulmasından sonra çizilen 2 nolu modelin grafiği aşağıda verilmiştir. Bu grafik rastgele orman modelinin sınıf hata (cevap değişkeni) oranlarını göstermektedir. Ağaç sayısı arttıkça hata oranı sıfıra yaklaşır.

2 nolu modeldeki değişkenlerin önem düzeyleri

k<-importance(model2)
ok<-k%>% as_tibble() 
ok<-ok[, c(5,6)]
ok
ok1<-tibble(Değişken=as.vector(row.names(k)), Ortalama_Doğruluk=ok$MeanDecreaseAccuracy,Ortalama_Gini=ok$MeanDecreaseGini )%>%mutate_if(is.numeric, round, 2)%>% arrange(desc(Ortalama_Gini))
formattable(ok1)
ogk<-ggplot(ok1, aes(x=Ortalama_Gini, y = Değişken, label=round(Ortalama_Gini,2)))+
   geom_point(color="red")+
    xlab("Ortalama Gini")+
    ylab("Değişken")+
    geom_text(vjust = 0, nudge_y = 0.1)
odk<-ggplot(ok1, aes(x=Ortalama_Doğruluk, y = Değişken, label=round(Ortalama_Doğruluk,2)))+
   geom_point(color="blue")+
    xlab("Ortalama Doğruluk")+
    ylab("Değişken")+
    geom_text(vjust = 0, nudge_y = 0.1)
ggarrange(ogk, odk, nrow=2)

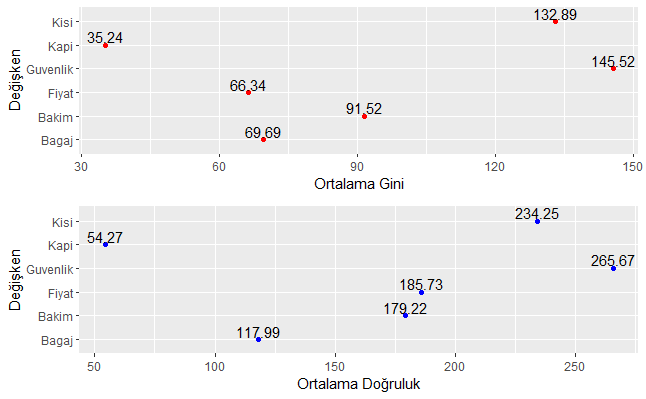
Yukarı kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeyleri ortalama gini katsayısına göre büyükten küçüğe doğru aşağıdaki tabloda verilmiştir.

Yukarı kod bloğunun çalıştırılmasından sonra elde edilen modeldeki değişkenlerin önem düzeylerine ilişkin grafik ise aşağıda verilmiştir.

Tahmin edilen değerler ile gözlem değerlerinin karşılaştırılması

pred1<-predict(model2, test1)
karsilastirma2<-tibble(Gercek=test1$Karar, Tahmin=pred2)
#ilk ve son 10 tahmin değerini gerçek değerle karşılaştırma 
ilk10<-head(karsilastirma2, 10) %>% rename(Gercekİlk_10=Gercek, Tahminİlk_10=Tahmin)
son10<-tail(karsilastirma2, 10) %>% rename(GercekSon_10=Gercek, TahminSon_10=Tahmin)
formattable(cbind(Id=seq(1,10),ilk10, son10))

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modelden elde edilen ilk ve son 10 sınıflandırma değerleri gerçekleşen sınıflandırma değerleri ile birlikte aşağıdaki tabloda karşılaştırmalı olarak verilmiştir.

Karışıklık matrisi (confusion matrix)’nin oluşturulması

pred2<-predict(model2, test1)
karsilastirma<-tibble(Gercek=test1$Karar, Tahmin=pred2)
#alternatif cm ve grafik
cm <- karsilastirma %>%
  conf_mat(Gercek, Tahmin)
cm
autoplot(cm, type = "heatmap")

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisi aşağıda verilmiştir.

 Truth
Prediction Kabul İyi Red Çok İyi
   Kabul     119   3   2       0
   İyi         0  24   2       0
   Red         6   0 347       0
   Çok İyi     1   0   0      14

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen karışıklık matrisinin grafiği ise aşağıda verilmiştir.

Hata parametreleri

Kurulan 1 nolu modele ait hata parametrelerinin elde edilmesine yönelik yazılan R kod bloğu aşağıda verilmiştir.

cm<-confusionMatrix(karsilastirma2$Tahmin, karsilastirma2$Gercek)
cm

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 1 nolu modele ait hata parametre değerleri aşağıda verilmiştir.

Confusion Matrix and Statistics
          Reference
Prediction Kabul İyi Red Çok İyi
   Kabul     119   3   2       0
   İyi         0  24   2       0
   Red         6   0 347       0
   Çok İyi     1   0   0      14
Overall Statistics
                                          
               Accuracy : 0.973           
                 95% CI : (0.9551, 0.9851)
    No Information Rate : 0.6776          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.9433          
                                          
 Mcnemar's Test P-Value : NA              
Statistics by Class:
                     Class: Kabul Class: İyi Class: Red Class: Çok İyi
Sensitivity                0.9444    0.88889     0.9886        1.00000
Specificity                0.9872    0.99593     0.9641        0.99802
Pos Pred Value             0.9597    0.92308     0.9830        0.93333
Neg Pred Value             0.9822    0.99390     0.9758        1.00000
Prevalence                 0.2432    0.05212     0.6776        0.02703
Detection Rate             0.2297    0.04633     0.6699        0.02703
Detection Prevalence       0.2394    0.05019     0.6815        0.02896
Balanced Accuracy          0.9658    0.94241     0.9763        0.99901

Bağımlı değişken kategorilerine göre sınıflandırma metrikleri

cm<-confusionMatrix(karsilastirma2$Tahmin, karsilastirma2$Gercek)
cm
class<-cm$byClass#sınıfa göre hata oranları
class<-class %>% as_tibble(class) %>% add_column(Class = c("Kabul", "İyi", "Red", "Çok İyi"), .before = "Sensitivity")
class
class1<-class[, c(1, 2,3,6, 7, 8)]
pivot<-class1 %>% pivot_longer(-Class, names_to = "Parameters", values_to = "Değer")
ggplot(pivot, aes(x="", y = Değer, fill = Class))+
geom_bar(position="stack", stat="identity")+
scale_fill_viridis(discrete = T, option = "E")+
facet_grid(Class~  Parameters)+
xlab("")+
labs(fill = "Kategori")

Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen bağımlı değişken kategorilerine göre sınıflandırma metrikleri aşağıdaki grafikte verilmiştir.

Çapraz performans testi (Cross validation test)

set.seed(12)
cv<- performanceEstimation(
  PredTask(Karar ~ ., df1[,-1]),
    workflowVariants(learner="randomForest", learner.pars=list(ntree = 500, mtry = 6, importance = TRUE)),
 EstimationTask(metrics = c("acc","err"),
                method = CV(nReps = 1, nFolds = 10)))
summary(cv)
plot(cv)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

== Summary of a  Cross Validation Performance Estimation Experiment ==
Task for estimating  acc,err  using
 1 x 10 - Fold Cross Validation
	 Run with seed =  1234 
* Predictive Tasks ::  df1[, -1].Karar
* Workflows  ::  randomForest 
-> Task:  df1[, -1].Karar
  *Workflow: randomForest 
               acc         err
avg     0.98255814 0.017441860
std     0.01162791 0.011627907
med     0.98837209 0.011627907
iqr     0.02180233 0.021802326
min     0.96511628 0.005813953
max     0.99418605 0.034883721
invalid 0.00000000 0.000000000

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değeri aşağıdaki grafikte verilmiştir.

Yeniden örnekleme (bootstrapping) perfomans kontrolü testi

set.seed(1234)
bootstrap <- performanceEstimation(
  PredTask(Karar ~ ., df1[,-1]),
    workflowVariants(learner="randomForest", learner.pars=list(ntree = 500, mtry = 6, importance = TRUE)),
  EstimationTask(metrics=c("err", "acc"),method=Bootstrap(nReps=100)))
summary(bootstrap)
topPerformers(bootstrap)
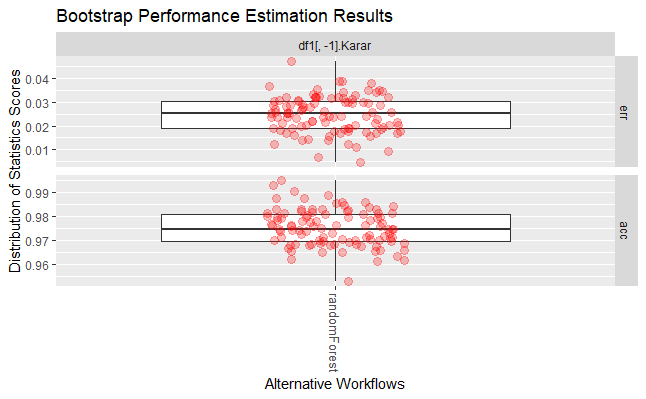
plot(bootstrap)

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

== Summary of a  Bootstrap Performance Estimation Experiment ==
Task for estimating  err,acc  using
100  repetitions of  e0  Bootstrap experiment
	 Run with seed =  1234 
* Predictive Tasks ::  df1[, -1].Karar
* Workflows  ::  randomForest 
-> Task:  df1[, -1].Karar
  *Workflow: randomForest 
                err         acc
avg     0.024709802 0.975290198
std     0.007599525 0.007599525
med     0.025197100 0.974802900
iqr     0.011384685 0.011384685
min     0.004680187 0.952978056
max     0.047021944 0.995319813
invalid 0.000000000 0.000000000

Yukarıdaki R kod bloğunun çalıştırılmasından sonra 2 nolu modele ait elde edilen performans parametre değerleri aşağıda verilmiştir.

Sonuç

Bu çalışmada sınıflandırma (classification) probleminin çözümüne yönelik Rastgele Orman (RF) algoritması kullanılarak ayrıntılı deneysel bir çalışma yapılmıştır. Ortaya konulan bulgular, sınıflandırma probleminin RF algoritması tarafından çok başarılı bir şekilde, diğer bir ifadeyle çok yüksek bir doğruluk oranıyla çözüme kavuşturulduğu görülmektedir.

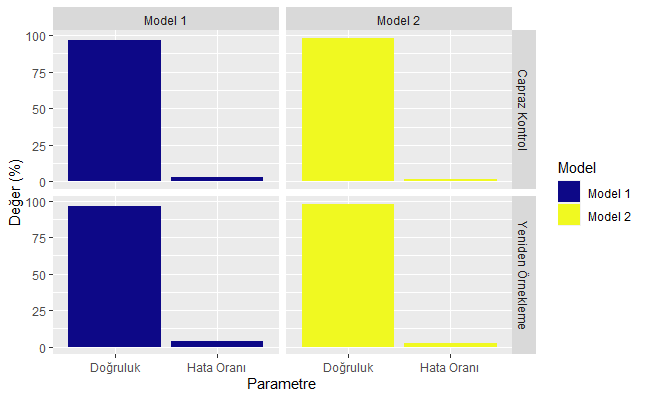
Her iki Rastgele Orman modeli (Model 1 ve 2) performans ölçüleri açısından karşılaştırıldığında öne çıkan bulgular şöyledir: Kurulan 2. model 1. modele göre bağımlı değişken olan “Karar” değişkenini daha iyi tahmin etmektedir. Model 2’de doğruluk (accuracy) oranı performans ölçüm metotlarından capraz kontrol (cross validation)’de % 98,26 iken, model 1’de bu oran % 96,86’da kalmıştır. Aşağıdaki tabloda her iki modelin hata ve doğruluk oranları verilmiştir. Performans ölçüm metotlarından yeniden örnekleme (bootstrapping) kullanıldığında model 2’den üretilen doğruluk oranı % 97,53 (yaklaşık % 98) iken bu oran model 1’de % 96,02’dir. Tabloda belirtilen hata (error) oranı 1-Doğruluk eşitliğinden hesaplanmaktadır. Buradan doğruluk oranı artıkça hata oranının azalacağı anlamı çıkarılması gerekir.

Yukarıdaki tablonun elde edilmesine yönelik yazılan R kod bloğu aşağıdadır. Aşağıdaki kod bloğunda aynı zamanda yukarıdaki tabloda verilen parametreler aşağıda yazılan kod bloğu aracılığıyla grafiğe taşınmıştır.

model1<-tibble(Model=rep("Model 1", 4), Performans_Metodu= c(rep("Capraz Kontrol",2), rep("Yeniden Örnekleme",2)), Parametre=rep(c("Doğruluk", "Hata Oranı"),2), Değer=c(round(0.96860465*100,2),round(0.03139535*100,2), round(0.960160679*100,2), round(0.039839321*100,2)))
         
model2<-tibble(Model=rep("Model 2", 4), Performans_Metodu= c(rep("Capraz Kontrol",2), rep("Yeniden Örnekleme",2)), Parametre=rep(c("Doğruluk", "Hata Oranı"),2), Değer=c(round(0.98255814*100,2),round(0.017441860*100,2), round(0.975290198*100,2), round(0.024709802*100,2)))
modeltum<-bind_rows(model1, model2)
formattable(modeltum)
  ggplot(modeltum, aes(x=Parametre, y = Değer, fill = Model))+
  geom_bar(position="stack", stat="identity")+
  scale_fill_viridis(discrete = T, option = "C")+
  facet_grid(Performans_Metodu~ Model)+
  xlab("Parametre")+
  ylab("Değer (%)")
  labs(fill = "Kategori")

Yukarıdaki R kod bloğunun çalıştırılmasından sonra kurulan her iki Rastgele Orman (RF) modeli hata metrikleri açısından aşağıdaki grafikte karşılaştırılmıştır.

Yapılan bu çalışmanın özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına önemli bir katkı sunacağı düşünülmektedir.

Faydalı olması ve farkındalık oluşturması dileğiyle.

Bilimle ve teknolojiyle kalınız.

Saygılarımla.

Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.

Note: It can not be cited or copied without referencing.

Yararlanılan Kaynaklar