Normal Dağılım Eğrisi Altındaki Alanların ve Bir Fonksiyonun Grafiği

Mart 14 2022

Çalışma kapsamında normal dağılım gösteren veri setlerinde normal dağılım eğrisi altında kalan alanın gösterimi ve fonksiyon grafiği oluşturma üzerine uygulamalar yapılmıştır. Bu amaçla ggplot2 ve tigerstats kütüphaneleri kullanılmıştır.

Yüklenen kütüphaneler

kütüphane<-c("dplyr","tibble","tidyr","tigerstats","kableExtra", "ggplot2", "cowplot", "ggtext", "ggthemes", "stargazer")
yükle<-sapply(kütüphane, require, character.only = TRUE, warn.conflicts = FALSE)

#Kütüphane yüklenme durumunu gösteren tablo
 
tibble(Sıra=1:length(kütüphane), Kütüphane=names(yükle), Durumu=as.logical(yükle)) %>% 
mutate(Durumu=if_else(Durumu==TRUE, "Yüklendi", "Paket Kurulumu Gerekli")) %>% 
stargazer(summary=FALSE, rownames=FALSE, type = "text", title = "Yüklenen Kütüphaneler")

Yüklenen Kütüphaneler
========================
Sıra Kütüphane   Durumu 
------------------------
1      dplyr    Yüklendi
2      tibble   Yüklendi
3      tidyr    Yüklendi
4    tigerstats Yüklendi
5    kableExtra Yüklendi
6     ggplot2   Yüklendi
7     cowplot   Yüklendi
8      ggtext   Yüklendi
9     ggthemes  Yüklendi
10   stargazer  Yüklendi
------------------------

Örnek 1

Bir üniversiteye giriş sınavının test puanlarının normal bir dağılıma uyduğunu varsayalım. Ortalama test puanı 300 ve standart sapma 89’dur. Sınavda 350 ve üzeri puan alan öğrencilerin yüzdesi nedir?

set.seed(1)
sonuc=pnorm(350, mean=300, sd=89, lower.tail=FALSE)
paste("Çözüm: Üniversiteye giriş sınavında 350 ve üzeri puan alan öğrencilerin oranı ",  "%", round(100*sonuc,2),"'dir.", sep="")

[1] "Çözüm: Üniversiteye giriş sınavında 350 ve üzeri puan alan öğrencilerin oranı %28.71'dir."

Örnek 1: Grafik üzerinde gösterim

pnormGC(350, region="above", mean=300, sd=89,graph=TRUE)

Örnek 2

Bir üniversiteye giriş sınavının test puanlarının normal bir dağılıma uyduğunu varsayalım. Ortalama test puanı 300, Standart sapması ise 89’dur. Sınavda 350 ve aşağı puan alan öğrencilerin yüzdesi nedir?

set.seed(1)
sonuc=pnorm(350, mean=300, sd=89, lower.tail=TRUE)
paste("Çözüm: Üniversiteye giriş sınavında 350 ve aşağı puan alan öğrencilerin oranı ",  "%", round(100*sonuc,2),"'dur.", sep="")

[1] "Çözüm: Üniversiteye giriş sınavında 350 ve aşağı puan alan öğrencilerin oranı %71.29'dur"

Örnek 2: Grafik üzerinde gösterim

pnormGC(350, region="below", mean=300, sd=89,graph=TRUE)

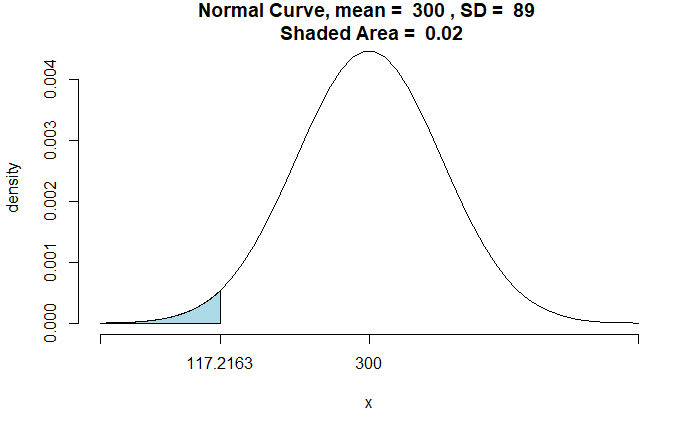
Örnek 3

Örneğin, ortalaması 300 ve standart sapması 89 olan bir normal dağılımın yüzde 2’lik dilimini bulmak istediğinizi varsayalım. Elde edilen 117.2163 değeri, ortalaması 300 ve standart sapması 89 ile normal dağılım gösteren bir popülasyondaki değerlerin %2’sinin 117,2163’nin altında olduğunu göstermektedir.

qnorm(0.02,mean=300,sd=89)

[1] 117.2163

Örnek 3: Grafik üzerinde gösterim

pnormGC(117.2163,region="below",mean=300, sd=89, graph=TRUE)

Standart normal dağılım grafiği I

Burada ortalaması 0, standart sapması 1 olan standart normal dağılım grafiği çizilmiştir.

pnormGC(c(-1.96,1.96),region="between",mean=0, sd=1,graph=TRUE)

Standart normal dağılım grafiği II

Bu kısımda ggplot2 kütüphanesi ve annotate() fonksiyonu kullanılarak standart normal dağılım grafiği çizilmiş, eğrinin altına ise fonksiyonu yazdırılmıştır.

nd <- ggplot(data.frame(x = c(-3,3)), aes(x = x)) +
  stat_function(fun = dnorm)
  nd +
  annotate("text", x = 0, y = 0.05, parse = TRUE, size = 4,
           label = "'Fonksiyon:  ' * y==frac(1, sqrt(2*pi)) * e^{-x^2/2}")+
  theme_bw() +

 ggtitle("Standart Normal Dağılım Grafiği")

Popülasyondan örneklem seçimi

library(DT)
data(imagpop) #veri seti
set.seed(61)#aynı sonuçları almak için
popsamp(10,imagpop) %>% datatable()

Bir fonksiyonun grafiğini çizme I

Aşağıdaki grafikte [-10, 10] x ekseni değerleri üzerinden $X^3-5X^2$ fonksiyonun baz grafiği çizilmiştir.

curve(x^3 - 5*(x)^2, from = -10, to = 10)

Bir fonksiyonun grafiğini çizme II

Bu kısımda fonksiyon grafiği için ggplot kütüphanesi kullanılmıştır. Aşağıdaki grafikte [-10, 10] x ekseni değerleri üzerinden $X^3-5X^2$ fonksiyonun grafiği çizilmiştir.

baz <-
  ggplot() +
  xlim(-10, 10)
baz + geom_function(fun = function(x) x^3 - 5*(x)^2, color="red", size=1.5)+
annotate("text", x = 0, y = -500, parse = TRUE, size = 4,
           label = "italic(y)==X^3-5*x^2")

#Alternatif

f <- function(x) {
              x^3 - 5*(x)^2}

ggplot(data.frame(x = c(-10, +10)), aes(x = x)) +
stat_function(fun = f, geom = "line", color="red", size=1.5) +
annotate("text", x = 0, y = -500, parse = TRUE, size = 4,colour = "darkblue",
           label = "italic(y)==X^3-5*x^2")

ggtext ve ggplot2 kütüphanesi ile ızgara grafik oluşturma

ggplot(iris, aes(Sepal.Width, Sepal.Length)) + 
  geom_point() +
  facet_wrap(~Species) +
  theme_half_open(12) +
  background_grid() +
  theme(
    strip.background = element_blank(),
    strip.text = element_textbox(
      size = 12,
      color = "black", fill = "#99ffff", box.color = "#4A618C",
      halign = 0.5, linetype = 1, r = unit(5, "pt"), width = unit(1, "npc"),
      padding = margin(2, 0, 1, 0), margin = margin(3, 3, 3, 3)
    )
  )

Sonuç

Özetle, bu çalışmayla normal dağılım gösteren veri setlerinde normal dağılım eğrisi altında kalan alanın gösterimi ve fonksiyon grafiği oluşturma üzerine uygulamalar yapılmıştır. Ayrıca çok yalın bir şekilde popülasyondan örneklem seçimi konusu ele alınmıştır.

Faydalı olması dileğiyle.

Bilimle ve teknolojiyle kalınız.

Önceki yazı Sonraki Yazı

Yorum Yaz