Güven aralıkları ingilizce ifadeyle confidence interval (CI) hem sahadan veri toplama yöntemleriyle elde edilen birincil verilerin hem de veri tabanlarından elde edilen işlenmiş ikincil verilerin analizinde çok yoğun bir şekilde kullanılmaktadır. Peki nedir bu güven aralığı? Güven aralığının hesaplanması için hangi parametrelere ihtiyaç vardır? Güven aralığı nasıl hesaplanır? Güven aralığını etkileyen faktörler nelerdir? Bu çalışmada bahsedilen bu sorulara cevaplar bulunacaktır. Bu amaçla olasılıklı örneklem yöntemlerinden biri olan ön yargısız (without bias) basit tesadüfi tekrarlı örneklem yöntemi kullanılarak yine aynı yöntemle üretilen rastgele beden kitle endeksi verileri üzerinden deneysel güven aralığı çalışması hazırlanmıştır. Diğer programlama dilleri kullanılarak veya paket programlar üzerinde de yapılabilmekle birlikte Microsoft Office Excel 2016 kullanılarak güven aralığı çalışması yapılmıştır. Bunun nedeni okuyucuya fonksiyon (formül) etkileşimlerinin gösterilerek daha fazla katkı sunulması amaçlanmasıdır. İki farklı güven aralığı çalışmasına yer verilmiştir. İlkinde güven aralığı çalışmasında elde edilen değerler sabitlenmiştir. İkincisinde ise simülasyona izin verecek dinamik bir şekilde excel uzantılı dosya içerisinde sunulmuştur. Bunun nedeni seçilen örneklemlerdeki parametre ve güven aralıkları değişimlerinin karşılaştırmalı olarak sunulması ve daha kolay anlaşılmasının sağlanmak istenmesidir.
Güven aralığı nedir?
Maliyetlerin yüksekliği, uzun zaman alması, güncel ve derinlemesine veri elde edilmesi gibi temel öncelikler esas alınarak sıklıkla kişiler ya da kurumlar popülasyonun tamamının yerine bu popülasyonu temsil eden örneklem üzerinde araştırma yapmayı tercih ederler. Ancak seçilen örneklemin popülasyonun tamamını temsil etmesi isteniyorsa yeterli örneklem büyüklüğü (n) belirlenerek mutlaka olasılıklı örneklem yöntemlerinden biri veya birkaçı birlikte kullanılmalıdır. Popülasyonun tamamı yerine bu popülasyondan seçilen örneklem söz konusu olunca örneklem popülasyonu ne kadar temsil ediyor soruyu ortaya çıkmaktadır. Güven aralığı ise aslında tam da bize bunu söylemektedir. Güven aralığı, popülasyon ortalamasının tahmincisi olup, bize örneklem ortalamalarının popülasyon ortalamasından ne kadarlık bir sapma olduğunu göstermektedir. Güven aralığının bir alt limit (lower bound)’i ve üst limit (upper bound)’i vardır. Bu alt ve üst limitlerin olması güven aralığına adını vermektedir. Yani örneklemden elde edilen güven aralıkları popülasyon ortalamasını mutlaka içerecektir. Burada güven aralığındaki alt ve üst limitin yorumlanması önem arz etmektedir. Alt ve üst limitler arasında fark ne kadar az ise, diğer bir deyişle güven aralığı genişliği (CI Width) ne kadar dar ise örneklem ortalaması popülasyon ortalamasına o kadar yakın ve örneklem ortalamasını o kadar doğru tahmin ediyor demektir. Tersi bir durum, örneklem ortalamasının popülasyon ortalamasından uzaklaşması anlamı taşımaktadır ki, bu durum örneklemin popülasyonu kötü temsili anlamına gelmektedir.
Güven aralığının hesaplanması için hangi parametrelere ihtiyaç vardır?
Genel olarak, güven aralığını hesaplamak için adım adım ele alınması gereken parametreler Şekil 1’de verilmiştir.
Şekil 1: Güven Aralığı Hesaplama Adımları

Şekil 1’de görüleceği üzere ilk olarak popülasyondan çekilen örneklemin ortalaması hesaplanır. Ortalama ise aşağıdaki eşitlik yardımıyla hesaplanmaktadır. Eşitlik örneklem ortalamasının hesaplanmasına yönelik olduğu için “X” parametresi kullanılmıştır. Örneklem ortalaması bütün gözlem değerlerinin toplamının toplam gözlem sayısına bölünmesi ile elde edilir. Eşitlikte küçük “n” örneklem büyüklüğünü ifade etmektedir.

Eğer popülasyon ortalamasını hesaplamış olsaydık eşitlikte n yerine büyük “N” e yer verecektik. Burada N popülasyondaki gözlem sayısını ifade etmektedir. Popülasyon ortalaması (μ) ise bütün gözlem değerlerinin toplamının toplam gözlem sayısı (N)’na bölünmesi ile elde edilmekte olup, aşağıdaki eşitlik yardımıyla hesaplanır.
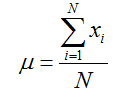
Örnekleme ait standart sapmanın hesaplanmasında ise aşağıdaki eşitlikten faydalanılır. Burada standart sapma ile aslında örneklem ortalamasından ne kadarlık bir sapma olduğunu gösteriyoruz. Adım adım örneklem standart sapması şöyle hesaplanır:
- Örneklemdeki gözlem değerlerinin ortalaması hesaplanır.
- Her bir gözlemin gözlem ortalamasından farkı alınır.
- Her bir gözleme ait hesaplanan farkın karesi hesaplanır.
- Her bir gözleme ait hesaplanan farkların karesi toplanır.
- Elde edilen fark kareleri toplamı örneklemdeki gözlem sayısının bir eksiğine bölünür.
- Son olarak elde edilen değerin karekökü hesaplanır.

Popülasyon standart sapmasının hesaplanması ise örneklem standart sapmasına benzer olup tek fark karekök içindeki eşitliğin paydasında büyük “N” e, diğer bir deyişle popülasyondaki toplam gözlem sayısına yer verilmesidir. Yukarıda örneklem standart sapmasındaki işlemler popülasyon standart sapması için de yapılır.

Element varyansı ise örneklem standart sapmasının karesi olup, aşağıdaki eşitlik yardımıyla hesaplanmaktadır.
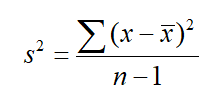
Eğer örneklemin popülasyon içinde yüzdesi (f=(n/N) x 100) %5’ten büyükse örneklem varyansının hesaplanması ve bunun üzerinden standart hata hesaplanması yoluna gidilmelidir. Örneklem varyansı ise aşağıdaki eşitlik yardımıyla hesaplanır.
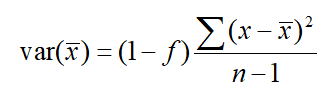
Popülasyon varyansı ise popülasyon standart sapmasının karesinin alınması ile hesaplanır. Aşağıdaki eşitlik yardımıyla popülasyon varyansı hesaplanır.

Standart hata (se), diğer bir ifade ile ortalamanın standart hatası aşağıdaki eşitlik yardımıyla hesaplanmaktadır. Örneklemin standart sapması (s)’nın karekök içerisindeki örneklem gözlem sayısı (n)’na bölünmesi bize ortalamanın standart hatası (standard error of the mean)’nı verir. Örneklem büyüklüğünün artırılması merkezi limit teoremi (central limit teorem)’ne dayalı olarak standart hatayı azaltır ve bu istenen bir durumdur. Böylece, örneklem dağılımı standart normal dağılıma (ortalaması 0, standart sapması 1) evrilir.

Güven aralığı nasıl hesaplanır?
Güven aralığının belirlenmesini sağlayan eşitliklere yer verildikten sonra sırasıyla şimdi çok yalın bir şekilde güven aralığı eşitliğini alt ve üst limitten başlayarak verelim. Bu çalışmada güven aralığı, ortalaması ve standart sapması bilinen bir popülasyon üzerinden hesaplanmıştır.
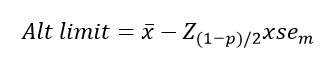

Güven aralığının alt ve üst limitini verdikten sonra bir bütün olarak güven aralığı (confidence interval) eşitliğini verelim. Eşitliğin ortasında yer verilen μ popülasyon ortalamasını göstermektedir. Daha önce de belirtildiği üzere güven aralıklarıyla aslında popülasyon ortalamasını tahmin ediyoruz.

Güven aralığının alt ve üst, diğer bir deyişle iki kuyruklu (two tailed) alfa katsayıları aşağıdaki şekil üzerinde verilmiştir. Z tablosu ortalaması 0, standart sapması 1 olan standart normal dağılımı kullanmaktadır. Standart normal dağılım eğrisi şeklinden dolayı can eğrisi (bell curve) olarak da adlandırılmaktadır. Eğrinin altında alanın toplamı 1’e eşittir. Burada belirlenen güven düzeyi % 95’tir. Bu güven düzeyi sosyal bilimler dışında özellikle sağlık bilimlerinde % 95’in üzerine çıkabilmektedir daha kesin çıkarımlar (inferences) alınmak istendiğinden.
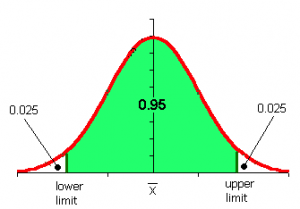
Güven aralığı eşitliğinde görüleceği üzere güven aralığının hesaplanması için gerekli parametreler örneklemin ortalaması, standart hatası (se) ve Z tablo değeridir. Burada Z tablo yerine pekala t (student’s t distribution) tablo değeri de alınabilirdi. Ancak örneklem büyüklüğümüz bu çalışma kapsamında 30’un üzerinde (n>30) olduğu için Z tablosu kullanılmıştır. Ancak isteğe bağlı olarak çalışmada 30’un altında örneklem büyüklüğü (n) belirlenerek t tablo değeri hesaplanabilir. Hem tekrarsız basit tesadüfi örnekleme (SRS without replacement) yöntemi hem de t tablo değerinin kullanılarak güven aralığı hesaplanmasına yönelik oluşturduğum simülasyon çalışmasına ise aşağıdaki linkten ulaşabilirsiniz.
Hem tekrarsız basit tesadüfi örnekleme (SRS without replacement) yöntemi hem de Z tablo değerinin kullanılarak güven aralığı hesaplanmasına yönelik oluşturduğum simülasyon çalışmasına ise aşağıdaki linkten ulaşabilirsiniz.
Diğer taraftan, genel olarak sosyal bilimlerdeki istatistiksel analiz ve araştırmalarda güven düzeyleri % 95 olarak alındığı için bu araştırmada da bu düzey benimsenmiştir. Güven düzeyinin % 95 olarak alınması % 5’lik hata payının kabul edildiğini göstermektedir. Hazırlamış olduğum çalışmalar, özellikle de simülasyon çalışması % 95 üzeri ve altı güven düzeyleri için de kolaylıkla uyarlanabilme özelliğine sahiptir.
Sırası gelmişken belirtmekte fayda olduğuna inanıyorum. Güven aralığının kamuoyunda ve literatürde sık sık yanlış yorumlandığı ve adlandırıldığı görülmektedir. Diğer bir deyişle, güven aralığı (confidence interval) ile güven düzeyi (confidence level) karıştırılmaktadır. Burada güven aralığı eğer yüzde olarak ifade edilmişse bu güven düzeyini, yüzde olarak ifade edilmemişse güven aralığını ifade etmektedir. % 95 güven düzeyine sahip olmak, sonuçlarınızın herkese anket yapmış gibi neredeyse aynı olduğundan emin olduğunuz anlamına gelir.
Güven aralığını etkileyen faktörler nelerdir?
Güven aralığını etkileyen faktörler şöyle sıralanabilir.
- Örneklem büyüklüğü: örneklem büyüklüğü (n) artıkça elde edilen cevapların popülasyonu doğrulama olasılığı o kadar artar. Diğer bir deyişle, örneklem büyüklüğünün artması güven aralığını daraltır. Ancak bu artış lineer olmayabilir.
- Örneklem seçiminde kullanılan yöntem: eğer örneklem olasıklı örneklem yöntemleri kullanılmadan ya da bu yöntemler kullanılsa bile hatalı örneklem seçimi yapılmışsa güven aralıklarını etkileyebilir. Dolayısıyla popülasyon parametresi olan ortalamalar doğru bir şekilde tahmin edilmemiş olur.
- Güven düzeyi (% 95’ten % 99’a yükselmesi) yükseldikçe güven aralığı genişler. Çünkü matematiksel olarak çarpım katsayısı da büyür. Örnek vermek gerekirse Z tablo değeri % 95 güven aralığında 1,96 iken güven aralığı = X-+1,96 x Standart Hata. Ancak Z tablo değeri % 99 güven aralığında 2,58 iken güven aralığı = X-+2,58 x Standart Hata olur.
- Örneklem ortalaması arttıkça güven aralığının genişliği aynı kalır. Dolayısıyla, örneklem ortalaması aralığın genişliğinde bir rol oynamaz.
- Örneklem standart sapmasının azalması varyansın azalması anlamına geldiğinden standart hata düşer. Bu durum güven aralığının daralmasına ve daha yüksek doğruluk (accuracy) ile popülasyon ortalamasının tahmini anlamına gelmektedir. Burada örneklem büyüklüğü ile standart hata arasında ters orantı vardır.
Güven aralığından yeterince bahsettikten sonra şimdi uygulama aşamasına geçebiliriz. Uygulamada kullanılan popülasyon veri seti beden kitle endeksi (BKİ) değerlerini içeren ve 1000 (N) gözlemden oluşan sentetik veri setidir. Olasılıklı örneklem yöntemlerinden basit tekrarlı tesadüfi örnekleme yöntemiyle 7 ve 50 aralığında BKİ değerleri üretilmiştir. BKİ değerleri üretilirken Sağlık Bakanlığı resmi web sitesindeki BKİ alt ve üst referans değerlerinden yararlanılmıştır. Burada belirlenen BKİ alt ve üst limitleri şöyledir:
| Parametre Değeri | Kategori |
| 8.5 kg/m2’nin altında ise | zayıf |
| 18.5-24.9 kg/m2 arasında ise | normal kilolu |
| 25-29.9 kg/m2 arasında ise | fazla kilolu |
| 30-34.9 kg/m2 arasında ise | I.Derece obez |
| 35-39.9 kg/m2 arasında ise | II.Derece obez |
| 40 kg/m2 üzerinde ise | III.Derece morbid obez |
İlk olarak popülasyondan her birinin örneklem büyüklüğü 31 olan 3 farklı örneklem çekilmiştir. Çekilen örneklemler popülasyondaki ID koduyla birlikte Tablo 1’de verilmiştir.
Tablo 1: Üç Farklı Örneklem Seçimi (n=31)
| ID1 | Örneklem1 | ID2 | Örneklem2 | ID3 | Örneklem3 | ||
| 23 | 48,01 | 24 | 18,11 | 68 | 32,87 | ||
| 22 | 31,82 | 90 | 30,13 | 60 | 11,73 | ||
| 56 | 41,07 | 61 | 43,58 | 84 | 41,64 | ||
| 57 | 10,66 | 82 | 19,04 | 68 | 32,87 | ||
| 98 | 42,07 | 41 | 20,02 | 30 | 49,89 | ||
| 63 | 12,44 | 48 | 17,6 | 9 | 34,97 | ||
| 81 | 18,76 | 47 | 31,9 | 85 | 30,5 | ||
| 95 | 34,55 | 24 | 18,11 | 25 | 27,06 | ||
| 57 | 10,66 | 67 | 9,48 | 69 | 31,2 | ||
| 82 | 19,04 | 98 | 42,07 | 5 | 7,76 | ||
| 17 | 39,17 | 22 | 31,82 | 15 | 12,08 | ||
| 10 | 9,01 | 17 | 39,17 | 75 | 31,55 | ||
| 19 | 31,9 | 96 | 36,16 | 49 | 46,61 | ||
| 93 | 10,34 | 78 | 14,76 | 11 | 22,15 | ||
| 5 | 7,76 | 5 | 7,76 | 68 | 32,87 | ||
| 69 | 31,2 | 89 | 32,92 | 68 | 32,87 | ||
| 75 | 31,55 | 95 | 34,55 | 81 | 18,76 | ||
| 92 | 17,95 | 98 | 42,07 | 40 | 27,74 | ||
| 89 | 32,92 | 78 | 14,76 | 33 | 11,46 | ||
| 17 | 39,17 | 71 | 40,09 | 67 | 9,48 | ||
| 31 | 12,15 | 73 | 18,22 | 83 | 48,09 | ||
| 48 | 17,6 | 13 | 41,63 | 39 | 18,04 | ||
| 5 | 7,76 | 32 | 28,52 | 19 | 31,9 | ||
| 58 | 48,9 | 99 | 30,76 | 23 | 48,01 | ||
| 50 | 18,95 | 50 | 18,95 | 52 | 16,68 | ||
| 6 | 49,39 | 7 | 46,01 | 40 | 27,74 | ||
| 95 | 34,55 | 77 | 15,45 | 15 | 12,08 | ||
| 16 | 38,02 | 19 | 31,9 | 81 | 18,76 | ||
| 60 | 11,73 | 65 | 7,69 | 95 | 34,55 | ||
| 66 | 29,01 | 67 | 9,48 | 37 | 11,01 | ||
| 87 | 11,02 | 60 | 11,73 | 13 | 41,63 |
Tablo 1’deki her bir örnekleme ait tanımlayıcı istatistikler Tablo 2’de verilmiştir. Tablo 1’de verilen tanımlayıcı istatistikler (descriptive statistics) standart sapma hariç aynı zamanda Şekil 3’teki kutu diyagram üzerinde yer alan parametre değerleridir.
Tablo 2: Örneklem Grubuna Göre Tanımlayıcı İstatistikler
| Parametre | Örneklem1 | Örneklem 2 | Örneklem3 | ||
| Ortalama | 25,78 | 25,95 | 27,57 | ||
| Standart Sapma | 13,69 | 12,09 | 12,58 | ||
| Minimum Değer | 7,76 | 7,69 | 7,76 | ||
| 1. Dörtte Birlik | 11,73 | 15,45 | 16,68 | ||
| 2. Dörtte Birlik (Medyan) | 29,01 | 28,52 | 30,50 | ||
| 3. Dörtte Birlik | 38,02 | 36,16 | 34,55 | ||
| Maksimum Değer | 49,39 | 46,01 | 49,89 | ||
| Fark (interquartile range) | 26,29 | 20,71 | 17,87 |
Tablo 2’de 3. dörtte birlik ve 1. dörtte birlik arasındaki değerlerin farkı alınarak çeyrekler arası aralık (interquartile range) hesaplanmıştır. 3. dörtte birlik ve 1. dörtte birlik aralığı uç değerleri (outliers) barındırmamaktadır. Bu aralıktaki veriler dışında veriler veri setinden çıkartılarak (imputation) analize devam edilebilir. Ancak bu durumda veri kaybı olacağı unutulmamalıdır. Yukarıda her bir örnekleme ait parametre değerleri kullanılarak (standart sapma hariç) her bir örneklem grubuna ait kutu diyagrama Şekil 3’te yer verilmiştir. Şekil 3’e esas teşkil eden tanımlayıcı istatistiklerin yukarıda verilmesinin nedeni kutu diyagram üzerindeki bu istatistiklerin yerinin karşılaştırmalı olarak gösterilmek istenmesidir. Böylece kutu diyagramların okunması ve anlaşılması daha da kolaylaştırılmış olur.
Şekil 3: Örneklem Grubuna Göre Kutu Diyagramlar (Box Plots)

Şekil 3’teki kutu diyagramdan öne çıkan bulgular şöyledir;
- Örneklem 3 diğer gruplara göre daha sola çarpıktır.
- Örneklem 1 diğer gruplara göre daha yüksek varyansa sahip ve daha az simetriktir. Varyansın bu grupta daha yüksek olduğu yukarıda tanımlayıcı istatistikler kısmında da yer verilen standart sapma değerinin yüksek olmasından da anlaşılabilir. Zira standart sapmanın karesi de varyansı bize vermektedir.
- Bütün örneklem gruplarında uç değerler (outliers) bulunmaktadır.
Güven aralıklarını vermeden önce popülasyona ait temel parametreleri vermekte fayda olduğu düşünülmektedir. Bu amaçla popülasyon parametre değerleri Tablo 3’te sunulmuştur.
Tablo 3: Popülasyon Parametreleri
| Popülasyon Parametreleri | Değer |
| Ortalama (µ) | 28,5 |
| Varyans | 148,0 |
| Standart Sapma | 12,2 |
Örneklem gruplarına ait üretilen güven aralıkları ise Tablo 4’te verilmiştir. Tablo 4’e göre öne çıkan bulgular şöyledir:
- Ortalamasının 27,6, ortalamanın standart hatasının (se) 2,1 olduğu örneklem3 grubu popülasyon ortalamasını en doğru tahmin eden grup olarak öne çıkmıştır. Bu grupta güven aralığı genişliği diğer gruplara göre daha dar olup “23,47 ≤ µ ≤31,67” şeklindedir. Buradan örneklem beden kitle endeksi ortalamasının % 95 olasılıkla 23,47 ile 31,67 arasında olduğunu söyleyebiliriz. Örneklem 3 grubunu ise güven aralığı genişliği (CI width) 11,1 olan örneklem2 grubu izlemiştir.
Tablo 3: Örneklem Grubuna Göre Güven Aralıkları
| Örneklem Parametreleri | Örneklem1 | Örneklem2 | Örneklem3 |
| Ortalama (m) | 25,8 | 25,9 | 27,6 |
| Element Varyans (s^2) | 181,3 | 141,5 | 153,1 |
| Standart Sapma (s) | 13,5 | 11,9 | 12,4 |
| Örneklem büyüklüğünün popülasyon içindeki yüzdesi (f) | 3,10 | 3,10 | 3,10 |
| Örneklem varyansı (var(x)) | 5,85 | 4,56 | 4,94 |
| Standart Hata (se) | 3,8 | 2,8 | 2,1 |
| Alfa (a/2) değeri (güven aralığının olasılık değeri) | 0,025 | 0,025 | 0,025 |
| Serbestlik derecesi (degrees of fredom) (n-1)-t tablosu | 30 | 30 | 30 |
| Z tablo değeri | 1,96 | 1,96 | 1,96 |
| %95 Güven Aralığı Alt Limit (Lower boundary of CI) | 18,3 | 20,4 | 23,5 |
| %95 Güven Aralığı Üst Limit (Upper boundary of CI | 33,3 | 31,5 | 31,7 |
| Güven Aralığı Genişliği (CI Width) | 15,0 | 11,1 | 8,2 |
| Güven aralığı gösterimi | 18,3 ≤ µ ≤33,26 | 20,39 ≤ µ ≤31,51 | 23,47 ≤ µ ≤31,67 |
| Karar | |||
| En iyi güven aralığına sahip örneklem | Örneklem 3 |
Güven aralıklarının yorumu
Güven aralıkları “popülasyon parametresinin alt limit ile üst limit arasında olduğundan %95 eminiz.” şeklinde yorumlanması gerekir. Burada %95 güven seviyesi %95 emin olabileceğimiz anlamına gelir. Bu güven düzeyi araştırma tasarımına bağlı olarak değişiklik ( %80, %90 ve %99 gibi) göstermekle birlikte sosyal bilimlerde genellikle %95’tir. Tablo 3’te örneklemlerin güven aralıklarını sırasıyla şöyle yorumlayabiliriz:
- Örneklem 1’in güven aralığının yorumu: Bu popülasyondaki tüm bireylerin popülasyonundaki ortalama BKİ değerleri 18,3 ile 33,26 arasında olduğundan %95 eminiz.
- Örneklem 2’inin güven aralığının yorumu: Bu popülasyondaki tüm bireylerin popülasyonundaki ortalama BKİ değerleri 20,39 ile 31,51 arasında olduğundan %95 eminiz.
- Örneklem 3’ün güven aralığının yorumu: Bu popülasyondaki tüm bireylerin popülasyonundaki ortalama BKİ değerleri 23,47 ile 31,67 arasında olduğundan %95 eminiz.
Tablo 3’teki güven aralıkları genişlikleri baz alınarak örneklem gruplarına göre güven aralıkları Şekil 4’te verilmiştir. Görüleceği üzere güven aralığı genişliği en dar olan örneklem grubu 8,2 ile örneklem 3 grubudur.
Şekil 4: Örneklem Gruplarına Göre Güven Aralığı Genişlikleri

Burada yapılan güven aralığı deneysel çalışmasının excel uzantılı dosyasını aşağıda linkten indirebilirsiniz.
Güven aralığının hesaplanmasına yönelik olarak hazırladığım simülasyonu ise aşağıdaki linkten indirebilirsiniz.
Farklı güven düzeylerinde güven aralıklarının hesaplanmasına yönelik olarak hazırladığım daha kapsamlı bir çalışmanın simülasyonunu aşağıdaki linkten indirebilirsiniz.
Z Tablosuna Göre Güven Aralığının Hesaplanmasına Yönelik Bir Simülasyon Çalışması
Yapılan bu çalışmaların özellikle veri bilimi (data science) ile ilgilenen akademi ve saha çalışanlarına bir katkı sunacağı düşünülmektedir.
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla…
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar
https://www.sbn.gov.tr/BKindeksi.aspx
https://www.statisticshowto.com/probability-and-statistics/confidence-interval/
http://www.stat.yale.edu/Courses/1997-98/101/confint.htm
https://researchbasics.education.uconn.edu/confidence-intervals-and-levels/
https://researchbasics.education.uconn.edu/confidence-intervals-and-levels/
https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/confidence-intervals
http://web.pdx.edu/~stipakb/download/PA551/boxplot.html
Field, Andy. (2009). Discovering Statistics Using SPSS. Third Edition.