Türkiye ekonomisinde döviz kuru oynaklıkları ve şokları iç ve/veya dış sebeplerden sıklıkla yaşanan bir durumdur. Bu çalışma kapsamında T.C. Merkez Bankası Dolar-TL alış kuru veri setinde farklı yöntemler kullanılarak Dolar-TL alış kuru 2020 dönem sonu tahminleri yapılmıştır. Dolar alış kuru tahmininde kullanılan ana değişken, 40 yıllık günlük “Dolar-TL alış kuru” değeridir.
Dolar kurunu etkileyen birçok farklı değişken modele sokularak dolar alış kurunun tahmin edilmesi elbette her zaman mümkündür. Bu durumda dolar kuru ve diğer değişkenler arasındaki nedensellik (causality) ilişkisi çok iyi bir şekilde ortaya konulmasından sonra model oluşturularak dolar kuru tahmini yapılabilir. Ortaya konulan bu değişkenlerin ölçülebilir olması da gereklidir. Ancak ölçülebilir olmayan nitel bir çok faktör de dolar kurunu etkileyebilmektedir. Örneğin uluslararası ilişkiler, iç siyasi ortam, terör, küresel ekonomik durgunluk gibi pek çok faktör de modele sokulup analiz edilmesi gereklidir. Ancak bu faktörler ölçülebilir olmadığından modele sokulması oldukça zordur ve çoğu zaman dışarda bırakılmaktadır. Dışarda bırakılan bu faktörler ölçülebilir olan nicel değişkenlerden daha da önemli de olabilir. Bu durumda sadece nicel ölçülebilir olan değişkenlerin modele sokulması eksik sonuçlar ortaya koyacaktır. Diğer bir konu, değişkenler belirlense bile bu değişkenlerin kendi içerisinde ve aralarındaki geçişkenlik dikkate alınması gereklidir.
Hacim olarak oldukça güvenilir 40 yıllık günlük Dolar-TL alış kuru veri setinin kullanılması başlı başına çok değerli çıkarımlar ortaya konulmasına katkı sağlayacaktır. Çünkü, ülkemizde döviz kuru dalgalanmaları, oynaklıkları ve şokları 40 yıllık bir zaman içerisinde bir döngü olarak sürekli yaşanmıştır. Dolayısıyla, döviz kurunu etkileyen faktörler zaten mevcut olan veri setinin içerisinde dolar alış kur değerlerine yansımış olduğu ve ekonomide öncü göstergelerden biri olduğu düşünülmektedir. Aynı zamanda bu nedenle bu çalışmada sadece dolar alış kurunun kendi içinde izlediği seyir dikkate alınarak model oluşturulmuştur. Oluşturulan model farklı yöntemlerle karşılaştırmalı olarak test edilerek MAPE (Mean Absolute Percentage Error) değerleri açsısından en iyi yöntemin hangisinin olduğuna karar verilmiştir. Deneysel olarak Merkez Bankası veri tabanından 02.01.1980 tarihinden 13.01.2020 tarihine kadar (dahil) indirilmiş dolar alış kuru verisi üzerinden 31.12.2020 tarihine kadar (dahil) geçen 353 günlük bir tahmin yapılması amaçlanmıştır. Tahminler yapılırken otomatik (default) olarak veri seti kullanılan yöntem içerisinde eğitilmiştir (training). Dolar alış kurunun tahmininde kullanılan yöntem (metot)’ler şöyledir:
- TBATS (Exponential smoothing state space model with Box-Cox transformation, ARMA errors, Trend and Seasonal components)
- ARIMA (Autoregressive Integrated Moving Average)
- ETS (Exponential Smoothing State Space Model)
- Naive
- NNAR (Neural Network Autoregression): Otoregresyon Sinir Ağı
- Holt
- SES (Simple Exponential Smoothing)
- Driftli Rassal Yürüyüş Yöntemi (Random Walk Forecast with Drift)
- Driftsiz Rassal Yürüyüş Yöntemi (Random Walk Forecast without Drift)
- Theta
Yukarıdaki bahsedilen yöntemlerle dolar alış kur değerleri tahmin edildikten sonra en iyi yöntem yaygın olarak kullanılan ve en güvenilir kabul edilen hata tiplerinden MAPE (Mean Absolute Percentage Error) ‘ye göre belirlenmiştir. MAPE hata değeri en düşük olan tahmin yöntemi Dolar-TL alış kuru tahminleri açısından en iyi yöntem olarak belirlenmiştir.
Merkez Bankası online veri tabanından 02.01.1980 tarihinden 13.01.2019 tarihine kadar (bu tarih dahil) olan günlük dolar alış kuru verisi xlsx olarak indirilmiştir. Veri setindeki değişken sayısı 2, gözlem sayı ise 10092’dir.
Çalışmada aynı zamanda tanımlayıcı istatistik bağlamında maksimum ve minimum kur değerleri esas alınarak yıllık ve aylık dalga boyları hesaplanarak grafikleri çizilmiştir. Dalga boyu, ilgili döneme ait maksimum dolar alış kuru değerinin minimum dolar alış kuru değerinden farkının minimum dolar alış kuru değerine bölünerek 100 ile çarpılmasını ifade etmektedir. Dalga boyu en yalın ifadeyle aşağıdaki eşitlik yardımıyla hesaplanmıştır: Dalga Boyu= (İlgili Döneme Ait Maksimum Kur Değeri-İlgili Döneme Ait Minimum Kur Değeri) / İlgili Döneme Ait Minimum Kur Değeri) X 100. Dalga boylarının hesaplanması döviz şoklarının gerçekleştiği dönemler ile ekonomik kriz dönemlerinin belirlenmesi açısından büyük öneme sahiptir.
İlk olarak R’da analiz için gerekli aşağıdaki kütüphaneler yüklenmiştir.
lapply(c("dplyr","tibble","tidyr","ggplot2","formattable","forecast","nnfor","xts","zoo","lubridate","readxl","xlsx"), require, character.only = TRUE)
Analiz kullanılan Merkez Bankası Dolar-TL alış kuru veri setine xlsx uzantılı olarak aşağıdaki linkte yer verilmiştir.
Analizde kullanılan Merkez Bankası Dolar Alış Kuru verisinin yüklenmesi için yazılan R kod bloğu aşağıda verilmiştir.
df <-read_excel("dolar.xlsx")
Veri setinin yüklenmesinden sonra veri setinin “tibble” tablo düzenine alınması ve tarih verisinin ay ve yıla dönüştürülmesi için gerekli R kod bloğuna aşağıda yer verilmiştir.
d1<-tibble(Tarih=dmy(df$Tarih), Yıl= year(dmy(df$Tarih)), Ay=month(df$Tarih), Kur=df$USD_Alis)
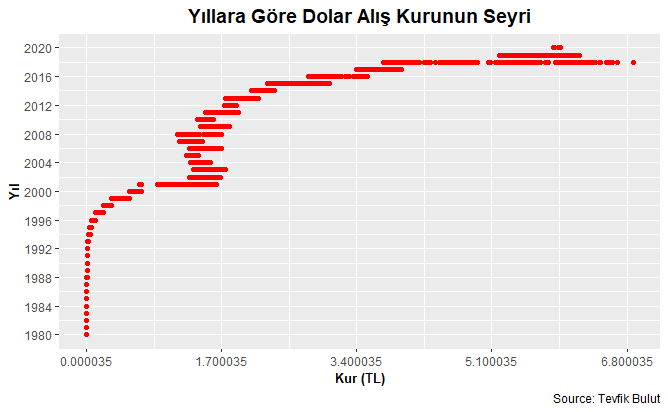
Veri setinden yıllara göre üretilen döviz alış kurunun seyrini gösteren grafiğe ilişkin R kod bloğu ise aşağıdadır.
d1%>%ggplot(aes(Kur, Yıl))+
geom_point(color="red")+
scale_y_continuous(breaks=seq(1980, 2020, 4))+
scale_x_continuous(breaks=seq(min(d1$Kur), max(d1$Kur),1.7))+
labs(caption = "Source: Tevfik Bulut")+
ggtitle("Yıllara Göre Dolar Alış Kurunun Seyri") +
xlab("Kur (TL)") + ylab("Yıl")+
theme(plot.title = element_text(family = "Trebuchet MS", face="bold",
size=14,hjust=0.5)) +
theme(axis.title = element_text(family = "Trebuchet MS", face="bold",
size=10))
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen yıllara göre dolar alış kuru seyri aşağıdaki grafikte verilmiştir.
Aylara göre döviz alış kurundaki maksimum ve minimum kur değerleri ile maksimum ve minimum kur farkının yüzdesel değişimi (Dalga Boyu)’ni hesaplamak için yazılan R kod bloğu aşağıdadır. Burada aynı zamanda tabloda yıl ve ayın olduğu sütunlar “Yilin_Ayi” adında birleştirilerek ayrı bir değişken olarak tanımlanmıştır.
ay<-d1 %>% group_by(Ay, Yıl)%>%summarise(Max_Kur=max(Kur), Min_Kur=min(Kur), Dalga_Boyu=((max(Kur)-min(Kur))/(min(Kur))*100))
ay$Yilin_Ayi<-paste(ay$Yıl,"-",ay$Ay)
ay
Dolar alış kurlarında aylık dalga boylarının en yüksek olduğu ayları içeren ilk 25 kayıt bulunduğu yılı içerek şekilde aşağıdaki kod bloğu ile verilmiştir.
k4<- ay %>% select(Yilin_Ayi, Dalga_Boyu)%>%
arrange(desc(Dalga_Boyu))
k5<- head(k4[, -1],20)
k5 %>% ggplot(aes(x=Yilin_Ayi, y=Dalga_Boyu))+
geom_area(size=2, color="red")+
theme(axis.text.x = element_text(face="bold",
size=8, angle=90),
axis.text.y = element_text(face="bold",
size=8, angle=90))+
geom_hline(yintercept=mean(k5$Dalga_Boyu), linetype="twodash", color =
"red", size=1)+
ggtitle("Döviz Alış Kuru Aylık Dalga Boyları") +
xlab("Yılın Ayı") + ylab("Dalga Boyu (%)")+
labs(caption = "Source: By Tevfik Bulut")+
theme(plot.title = element_text(family = "Trebuchet MS", face="bold",
size=16, hjust=0.5)) +
theme(axis.title = element_text(family = "Trebuchet MS", face="bold",
size=12))
Yukarıdaki kod bloğunun çalıştırılmasından sonra dolar alış kurlarında aylık dalga boylarının en yüksek olduğu ayları içeren ilk 20 kayıt bulunduğu yılı içerek şekilde aşağıdaki grafikte verilmiştir. Aşağıdaki şekilde x eksenine yatay yeşil çizgi dalga boylarının ortalamasını göstermektedir.

Dolar alış kurlarında yıllık dalga boylarının en yüksek olduğu ilk 20 kayıt aşağıdaki kod bloğu ile verilmiştir.
yil<-ay %>% select(Yıl, Dalga_Boyu)%>%
arrange(desc(Dalga_Boyu))
ydb<-head(yil[,-1],20)
ydb %>% ggplot(aes(x=Yıl, y=Dalga_Boyu))+
geom_line(arrow = arrow(angle = 15, ends = "both", type =
"closed"),size=2, color="brown")+
scale_x_continuous(breaks=seq(1980, 2020, 2))+
theme(axis.text.x = element_text(face="bold",
size=8, angle=90),
axis.text.y = element_text(face="bold",
size=8, angle=90))+
geom_hline(yintercept=mean(ydb$Dalga_Boyu), linetype="twodash",
color = "green", size=2)+
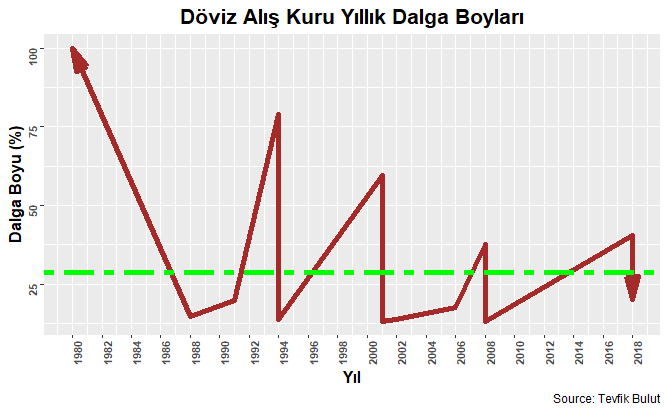
ggtitle("Döviz Alış Kuru Yıllık Dalga Boyları") +
xlab("Yıl") + ylab("Dalga Boyu (%)")+
labs(caption = "Source: Tevfik Bulut")+
theme(plot.title = element_text(family = "Trebuchet MS",
face="bold", size=16, hjust=0.5)) +
theme(axis.title = element_text(family = "Trebuchet MS",
face="bold", size=12))
Yukarıdaki kod bloğunun çalıştırılmasından sonra dolar alış kurlarında yıllık dalga boylarının en yüksek olduğu ilk 25 kayıt aşağıdaki şekilde verilmiştir. Şekilde x eksenine yatay yeşil çizgi dalga boylarının ortalamasını göstermektedir. Şekilde verilen Dolar-TL alış kurundaki dalga boyları Türkiye’deki döviz şoklarını ve ekonomik kriz dönemlerini net bir şekilde ortaya koymaktadır.
Veri seti tahmin yöntemlerinde kullanılmak üzere zaman serisine formatına dönüştürülmüştür. Yapılan bu işleme ilişkin R kod bloğu aşağıda verilmiştir.
y10<-as.Date(df$Tarih, format = "%d - %m - %Y")
tev<-ts(as.vector(df[,2]), as.vector(y10))
data <- msts(tev,seasonal.periods=c(7,365.25))
TBATS Yöntemi
Dolar alış kurunun tahmininde kullanılan ilk yöntem TBATS olup, bu yönteme ilişkin algoritma aşağıdaki R kod bloğunda verilmiştir.
function (x)
{
if (!is.null(x$lambda)) {
y <- BoxCox(x$y, x$lambda)
lambda <- attr(y, "lambda")
}
else {
y <- x$y
}
tau <- ifelse(!is.null(x$k.vector), 2 * sum(x$k.vector),
0)
w <- .Call("makeTBATSWMatrix", smallPhi_s = x$damping.parameter,
kVector_s = as.integer(x$k.vector), arCoefs_s = x$ar.coefficients,
maCoefs_s = x$ma.coefficients, tau_s = as.integer(tau),
PACKAGE = "forecast")
out <- cbind(observed = c(y), level = x$x[1, ])
if (!is.null(x$beta)) {
out <- cbind(out, slope = x$x[2, ])
}
if (tau > 0) {
nonseas <- 2 + !is.null(x$beta)
nseas <- length(x$seasonal.periods)
seas.states <- cbind(x$seed.states, x$x)[-(1:(1 + !is.null(x$beta))),
]
seas.states <- seas.states[, -ncol(seas.states)]
w <- w$w.transpose[, -(1:(1 + !is.null(x$beta))), drop = FALSE]
w <- w[, 1:tau, drop = FALSE]
j <- cumsum(c(1, 2 * x$k.vector))
for (i in 1:nseas) out <- cbind(out, season = c(w[, j[i]:(j[i +
1] - 1), drop = FALSE] %*% seas.states[j[i]:(j[i +
1] - 1), ]))
if (nseas > 1) {
colnames(out)[nonseas + 1:nseas] <- paste("season",
1:nseas, sep = "")
}
}
out <- ts(out)
tsp(out) <- tsp(y)
return(out)
}
Şimdi sıra TBATS yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
data <- msts(tev,seasonal.periods=c(7,365.25))
model <- tbats(data)
sonuc<- forecast(model,h=353)
autoplot(sonuc) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("TBATS Yöntemi İle Tahmin Edilen Dolar Alış Kuru")
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))+
labs(caption = "Source: Tevfik Bulut")
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “tbats” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğunu aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(sonuc)
today4<-today3[, -2:-3]
tbats<-cbind(Tarih=today2, today4)
write.xlsx(tbats, file = "tbats.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
TBATS yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. MAPE değeri zaman serisi analizlerinden kullanılan ve modelin güvenilirliğinin ölçülmesinde sıklıkla başvurulan en güvenilir hata türlerinden birisidir. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra TBATS yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
data <- msts(tev,seasonal.periods=c(7,365.25))
model <- tbats(data)
sonuc<- forecast(model,h=353)
summary(sonuc)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere TBATS yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.4897634‘tür.
Forecast method: TBATS(0.049, {3,0}, -, {<7,3>, <365.25,8>})
Model Information:
TBATS(0.049, {3,0}, -, {<7,3>, <365.25,8>})
Call: tbats(y = data)
Parameters
Lambda: 0.049011
Alpha: 0.02034718
Gamma-1 Values: 0.0002026845 -0.0001234526
Gamma-2 Values: 0.0004084971 3.040264e-05
AR coefficients: 1.129051 -0.296009 0.156864
Seed States:
[,1]
[1,] -7.984000e+00
[2,] -2.453819e-04
[3,] -4.667024e-06
[4,] -1.400260e-04
[5,] -1.331329e-04
[6,] 6.942891e-05
[7,] -1.398736e-05
[8,] 1.230420e-02
[9,] 1.054255e-03
[10,] -1.711990e-03
[11,] -1.504480e-03
[12,] -4.977709e-03
[13,] -1.359871e-03
[14,] -3.872218e-04
[15,] -1.010010e-03
[16,] -4.394557e-03
[17,] 3.579392e-03
[18,] -6.306786e-05
[19,] -1.700927e-03
[20,] -1.410837e-03
[21,] 2.297299e-04
[22,] -6.422550e-04
[23,] -3.995525e-04
[24,] 0.000000e+00
[25,] 0.000000e+00
[26,] 0.000000e+00
attr(,"lambda")
[1] 0.04901073
Sigma: 0.01017209
AIC: -47840.15
Error measures:
ME RMSE MAE MPE MAPE
Training set 0.0002509627 0.01998889 0.006809487 0.05236497 0.4897634
MASE ACF1
Training set 0.02762049 0.009573125
ETS YÖNTEMİ
Dolar alış kurunun tahmininde kullanılan ikinci yöntem ETS olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, model = "ZZZ", damped = NULL, alpha = NULL,
beta = NULL, gamma = NULL, phi = NULL, additive.only = FALSE,
lambda = NULL, biasadj = FALSE, lower = c(rep(1e-04, 3),
0.8), upper = c(rep(0.9999, 3), 0.98), opt.crit = c("lik",
"amse", "mse", "sigma", "mae"),
nmse = 3, bounds = c("both", "usual", "admissible"),
ic = c("aicc", "aic", "bic"), restrict = TRUE,
allow.multiplicative.trend = FALSE, use.initial.values = FALSE,
na.action = c("na.contiguous", "na.interp", "na.fail"),
...)
{
opt.crit <- match.arg(opt.crit)
bounds <- match.arg(bounds)
ic <- match.arg(ic)
if (!is.function(na.action)) {
na.fn_name <- match.arg(na.action)
na.action <- get(na.fn_name)
}
seriesname <- deparse(substitute(y))
if (any(class(y) %in% c("data.frame", "list",
"matrix", "mts"))) {
stop("y should be a univariate time series")
}
y <- as.ts(y)
if (missing(model) && is.constant(y)) {
return(ses(y, alpha = 0.99999, initial = "simple")$model)
}
ny <- length(y)
y <- na.action(y)
if (ny != length(y) && na.fn_name == "na.contiguous") {
warning("Missing values encountered. Using longest contiguous portion of time series")
ny <- length(y)
}
orig.y <- y
if (identical(class(model), "ets") && is.null(lambda)) {
lambda <- model$lambda
}
if (!is.null(lambda)) {
y <- BoxCox(y, lambda)
lambda <- attr(y, "lambda")
additive.only <- TRUE
}
if (nmse < 1 || nmse > 30) {
stop("nmse out of range")
}
m <- frequency(y)
if (any(upper < lower)) {
stop("Lower limits must be less than upper limits")
}
if (class(model) == "ets") {
alpha <- max(model$par["alpha"], 1e-10)
beta <- model$par["beta"]
if (is.na(beta)) {
beta <- NULL
}
gamma <- model$par["gamma"]
if (is.na(gamma)) {
gamma <- NULL
}
phi <- model$par["phi"]
if (is.na(phi)) {
phi <- NULL
}
modelcomponents <- paste(model$components[1], model$components[2],
model$components[3], sep = "")
damped <- (model$components[4] == "TRUE")
if (use.initial.values) {
errortype <- substr(modelcomponents, 1, 1)
trendtype <- substr(modelcomponents, 2, 2)
seasontype <- substr(modelcomponents, 3, 3)
e <- pegelsresid.C(y, m, model$initstate, errortype,
trendtype, seasontype, damped, alpha, beta, gamma,
phi, nmse)
np <- length(model$par) + 1
model$loglik <- -0.5 * e$lik
model$aic <- e$lik + 2 * np
model$bic <- e$lik + log(ny) * np
model$aicc <- model$aic + 2 * np * (np + 1)/(ny -
np - 1)
model$mse <- e$amse[1]
model$amse <- mean(e$amse)
tsp.y <- tsp(y)
model$states <- ts(e$states, frequency = tsp.y[3],
start = tsp.y[1] - 1/tsp.y[3])
colnames(model$states)[1] <- "l"
if (trendtype != "N") {
colnames(model$states)[2] <- "b"
}
if (seasontype != "N") {
colnames(model$states)[(2 + (trendtype != "N")):ncol(model$states)] <- paste("s",
1:m, sep = "")
}
if (errortype == "A") {
model$fitted <- ts(y - e$e, frequency = tsp.y[3],
start = tsp.y[1])
}
else {
model$fitted <- ts(y/(1 + e$e), frequency = tsp.y[3],
start = tsp.y[1])
}
model$residuals <- ts(e$e, frequency = tsp.y[3],
start = tsp.y[1])
model$sigma2 <- sum(model$residuals^2, na.rm = TRUE)/(ny -
np)
model$x <- orig.y
model$series <- seriesname
if (!is.null(lambda)) {
model$fitted <- InvBoxCox(model$fitted, lambda,
biasadj, var(model$residuals))
attr(lambda, "biasadj") <- biasadj
}
model$lambda <- lambda
return(model)
}
else {
model <- modelcomponents
if (missing(use.initial.values)) {
message("Model is being refit with current smoothing parameters but initial states are being re-estimated.\nSet 'use.initial.values=TRUE' if you want to re-use existing initial values.")
}
}
}
errortype <- substr(model, 1, 1)
trendtype <- substr(model, 2, 2)
seasontype <- substr(model, 3, 3)
if (!is.element(errortype, c("M", "A", "Z"))) {
stop("Invalid error type")
}
if (!is.element(trendtype, c("N", "A", "M",
"Z"))) {
stop("Invalid trend type")
}
if (!is.element(seasontype, c("N", "A", "M",
"Z"))) {
stop("Invalid season type")
}
if (m < 1 || length(y) <= m) {
seasontype <- "N"
}
if (m == 1) {
if (seasontype == "A" || seasontype == "M") {
stop("Nonseasonal data")
}
else {
substr(model, 3, 3) <- seasontype <- "N"
}
}
if (m > 24) {
if (is.element(seasontype, c("A", "M"))) {
stop("Frequency too high")
}
else if (seasontype == "Z") {
warning("I can't handle data with frequency greater than 24. Seasonality will be ignored. Try stlf() if you need seasonal forecasts.")
substr(model, 3, 3) <- seasontype <- "N"
}
}
if (restrict) {
if ((errortype == "A" && (trendtype == "M" ||
seasontype == "M")) | (errortype == "M" &&
trendtype == "M" && seasontype == "A") ||
(additive.only && (errortype == "M" || trendtype ==
"M" || seasontype == "M"))) {
stop("Forbidden model combination")
}
}
data.positive <- (min(y) > 0)
if (!data.positive && errortype == "M") {
stop("Inappropriate model for data with negative or zero values")
}
if (!is.null(damped)) {
if (damped && trendtype == "N") {
stop("Forbidden model combination")
}
}
n <- length(y)
npars <- 2L
if (trendtype == "A" || trendtype == "M") {
npars <- npars + 2L
}
if (seasontype == "A" || seasontype == "M") {
npars <- npars + m
}
if (!is.null(damped)) {
npars <- npars + as.numeric(damped)
}
if (n <= npars + 4L) {
if (!is.null(damped)) {
if (damped) {
warning("Not enough data to use damping")
}
}
if (seasontype == "A" || seasontype == "M") {
fit <- try(HoltWintersZZ(orig.y, alpha = alpha, beta = beta,
gamma = gamma, phi = phi, exponential = (trendtype ==
"M"), seasonal = ifelse(seasontype !=
"A", "multiplicative", "additive"),
lambda = lambda, biasadj = biasadj, warnings = FALSE),
silent = TRUE)
if (!("try-error" %in% class(fit))) {
fit$call <- match.call()
fit$method <- as.character(fit)
fit$series <- deparse(substitute(y))
return(fit)
}
else {
warning("Seasonal component could not be estimated")
}
}
if (trendtype == "A" || trendtype == "M") {
fit <- try(HoltWintersZZ(orig.y, alpha = alpha, beta = beta,
gamma = FALSE, phi = phi, exponential = (trendtype ==
"M"), lambda = lambda, biasadj = biasadj,
warnings = FALSE), silent = TRUE)
if (!("try-error" %in% class(fit))) {
fit$call <- match.call()
fit$method <- as.character(fit)
fit$series <- deparse(substitute(y))
return(fit)
}
else {
warning("Trend component could not be estimated")
}
}
if (trendtype == "N" && seasontype == "N") {
fit <- try(HoltWintersZZ(orig.y, alpha = alpha, beta = FALSE,
gamma = FALSE, lambda = lambda, biasadj = biasadj,
warnings = FALSE), silent = TRUE)
if (!("try-error" %in% class(fit))) {
fit$call <- match.call()
fit$method <- as.character(fit)
fit$series <- deparse(substitute(y))
return(fit)
}
}
fit1 <- try(HoltWintersZZ(orig.y, alpha = alpha, beta = beta,
gamma = FALSE, phi = phi, exponential = (trendtype ==
"M"), lambda = lambda, biasadj = biasadj,
warnings = FALSE), silent = TRUE)
fit2 <- try(HoltWintersZZ(orig.y, alpha = alpha, beta = FALSE,
gamma = FALSE, phi = phi, exponential = (trendtype ==
"M"), lambda = lambda, biasadj = biasadj,
warnings = FALSE), silent = TRUE)
if ("try-error" %in% class(fit1)) {
fit <- fit2
}
else if (fit1$sigma2 < fit2$sigma2) {
fit <- fit1
}
else {
fit <- fit2
}
if ("try-error" %in% class(fit))
stop("Unable to estimate a model.")
fit$call <- match.call()
fit$method <- as.character(fit)
fit$series <- deparse(substitute(y))
return(fit)
}
if (errortype == "Z") {
errortype <- c("A", "M")
}
if (trendtype == "Z") {
if (allow.multiplicative.trend) {
trendtype <- c("N", "A", "M")
}
else {
trendtype <- c("N", "A")
}
}
if (seasontype == "Z") {
seasontype <- c("N", "A", "M")
}
if (is.null(damped)) {
damped <- c(TRUE, FALSE)
}
best.ic <- Inf
for (i in 1:length(errortype)) {
for (j in 1:length(trendtype)) {
for (k in 1:length(seasontype)) {
for (l in 1:length(damped)) {
if (trendtype[j] == "N" && damped[l]) {
next
}
if (restrict) {
if (errortype[i] == "A" && (trendtype[j] ==
"M" || seasontype[k] == "M")) {
next
}
if (errortype[i] == "M" && trendtype[j] ==
"M" && seasontype[k] == "A") {
next
}
if (additive.only && (errortype[i] == "M" ||
trendtype[j] == "M" || seasontype[k] ==
"M")) {
next
}
}
if (!data.positive && errortype[i] == "M") {
next
}
fit <- try(etsmodel(y, errortype[i], trendtype[j],
seasontype[k], damped[l], alpha, beta, gamma,
phi, lower = lower, upper = upper, opt.crit = opt.crit,
nmse = nmse, bounds = bounds, ...), silent = TRUE)
if (is.element("try-error", class(fit)))
fit.ic <- Inf
else fit.ic <- switch(ic, aic = fit$aic, bic = fit$bic,
aicc = fit$aicc)
if (!is.na(fit.ic)) {
if (fit.ic < best.ic) {
model <- fit
best.ic <- fit.ic
best.e <- errortype[i]
best.t <- trendtype[j]
best.s <- seasontype[k]
best.d <- damped[l]
}
}
}
}
}
}
if (best.ic == Inf) {
stop("No model able to be fitted")
}
model$m <- m
model$method <- paste("ETS(", best.e, ",", best.t,
ifelse(best.d, "d", ""), ",", best.s,
")", sep = "")
model$series <- seriesname
model$components <- c(best.e, best.t, best.s, best.d)
model$call <- match.call()
model$initstate <- model$states[1, ]
np <- length(model$par)
model$sigma2 <- sum(model$residuals^2, na.rm = TRUE)/(ny -
np)
model$x <- orig.y
if (!is.null(lambda)) {
model$fitted <- InvBoxCox(model$fitted, lambda, biasadj,
var(model$residuals))
attr(lambda, "biasadj") <- biasadj
}
model$lambda <- lambda
return(structure(model, class = "ets"))
}
Şimdi sıra ETS yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
ETS <- forecast(ets(data), h=353)
autoplot(ETS) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("ETS Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “ets” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğunu aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(ETS)
today4<-today3[, -2:-3]
ets<-cbind(Tarih=today2, today4)
write.xlsx(ets, file = "ets.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
ETS yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra ETS yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
ETS <- forecast(ets(data), h=353)
summary(ETS)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere ETS yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.505253‘tür.
Forecast method: ETS(M,Ad,N)
Model Information:
ETS(M,Ad,N)
Call:
ets(y = data)
Smoothing parameters:
alpha = 0.9999
beta = 0.0024
phi = 0.9782
Initial states:
l = 0
b = 0
sigma: 0.014
AIC AICc BIC
-43903.33 -43903.32 -43860.01
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0005255783 0.0204113 0.006772561 0.07816683 0.505253 0.02747071
ACF1
Training set 0.1603195
ARIMA Yöntemi
Dolar alış kurunun tahmininde kullanılan üçüncü yöntem ARIMA olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (x, order = c(0L, 0L, 0L), seasonal = list(order = c(0L,
0L, 0L), period = NA), xreg = NULL, include.mean = TRUE,
transform.pars = TRUE, fixed = NULL, init = NULL, method = c("CSS-ML",
"ML", "CSS"), n.cond, SSinit = c("Gardner1980",
"Rossignol2011"), optim.method = "BFGS",
optim.control = list(), kappa = 1e+06)
{
"%+%" <- function(a, b) .Call(C_TSconv, a, b)
SSinit <- match.arg(SSinit)
SS.G <- SSinit == "Gardner1980"
upARIMA <- function(mod, phi, theta) {
p <- length(phi)
q <- length(theta)
mod$phi <- phi
mod$theta <- theta
r <- max(p, q + 1L)
if (p > 0)
mod$T[1L:p, 1L] <- phi
if (r > 1L)
mod$Pn[1L:r, 1L:r] <- if (SS.G)
.Call(C_getQ0, phi, theta)
else .Call(C_getQ0bis, phi, theta, tol = 0)
else mod$Pn[1L, 1L] <- if (p > 0)
1/(1 - phi^2)
else 1
mod$a[] <- 0
mod
}
arimaSS <- function(y, mod) {
.Call(C_ARIMA_Like, y, mod, 0L, TRUE)
}
armafn <- function(p, trans) {
par <- coef
par[mask] <- p
trarma <- .Call(C_ARIMA_transPars, par, arma, trans)
if (is.null(Z <- tryCatch(upARIMA(mod, trarma[[1L]],
trarma[[2L]]), error = function(e) NULL)))
return(.Machine$double.xmax)
if (ncxreg > 0)
x <- x - xreg %*% par[narma + (1L:ncxreg)]
res <- .Call(C_ARIMA_Like, x, Z, 0L, FALSE)
s2 <- res[1L]/res[3L]
0.5 * (log(s2) + res[2L]/res[3L])
}
armaCSS <- function(p) {
par <- as.double(fixed)
par[mask] <- p
trarma <- .Call(C_ARIMA_transPars, par, arma, FALSE)
if (ncxreg > 0)
x <- x - xreg %*% par[narma + (1L:ncxreg)]
res <- .Call(C_ARIMA_CSS, x, arma, trarma[[1L]], trarma[[2L]],
as.integer(ncond), FALSE)
0.5 * log(res)
}
arCheck <- function(ar) {
p <- max(which(c(1, -ar) != 0)) - 1
if (!p)
return(TRUE)
all(Mod(polyroot(c(1, -ar[1L:p]))) > 1)
}
maInvert <- function(ma) {
q <- length(ma)
q0 <- max(which(c(1, ma) != 0)) - 1L
if (!q0)
return(ma)
roots <- polyroot(c(1, ma[1L:q0]))
ind <- Mod(roots) < 1
if (all(!ind))
return(ma)
if (q0 == 1)
return(c(1/ma[1L], rep.int(0, q - q0)))
roots[ind] <- 1/roots[ind]
x <- 1
for (r in roots) x <- c(x, 0) - c(0, x)/r
c(Re(x[-1L]), rep.int(0, q - q0))
}
series <- deparse(substitute(x))
if (NCOL(x) > 1L)
stop("only implemented for univariate time series")
method <- match.arg(method)
x <- as.ts(x)
if (!is.numeric(x))
stop("'x' must be numeric")
storage.mode(x) <- "double"
dim(x) <- NULL
n <- length(x)
if (!missing(order))
if (!is.numeric(order) || length(order) != 3L || any(order <
0))
stop("'order' must be a non-negative numeric vector of length 3")
if (!missing(seasonal))
if (is.list(seasonal)) {
if (is.null(seasonal$order))
stop("'seasonal' must be a list with component 'order'")
if (!is.numeric(seasonal$order) || length(seasonal$order) !=
3L || any(seasonal$order < 0L))
stop("'seasonal$order' must be a non-negative numeric vector of length 3")
}
else if (is.numeric(order)) {
if (length(order) == 3L)
seasonal <- list(order = seasonal)
else ("'seasonal' is of the wrong length")
}
else stop("'seasonal' must be a list with component 'order'")
if (is.null(seasonal$period) || is.na(seasonal$period) ||
seasonal$period == 0)
seasonal$period <- frequency(x)
arma <- as.integer(c(order[-2L], seasonal$order[-2L], seasonal$period,
order[2L], seasonal$order[2L]))
narma <- sum(arma[1L:4L])
xtsp <- tsp(x)
tsp(x) <- NULL
Delta <- 1
for (i in seq_len(order[2L])) Delta <- Delta %+% c(1, -1)
for (i in seq_len(seasonal$order[2L])) Delta <- Delta %+%
c(1, rep.int(0, seasonal$period - 1), -1)
Delta <- -Delta[-1L]
nd <- order[2L] + seasonal$order[2L]
n.used <- sum(!is.na(x)) - length(Delta)
if (is.null(xreg)) {
ncxreg <- 0L
}
else {
nmxreg <- deparse(substitute(xreg))
if (NROW(xreg) != n)
stop("lengths of 'x' and 'xreg' do not match")
ncxreg <- NCOL(xreg)
xreg <- as.matrix(xreg)
storage.mode(xreg) <- "double"
}
class(xreg) <- NULL
if (ncxreg > 0L && is.null(colnames(xreg)))
colnames(xreg) <- if (ncxreg == 1L)
nmxreg
else paste0(nmxreg, 1L:ncxreg)
if (include.mean && (nd == 0L)) {
xreg <- cbind(intercept = rep(1, n), xreg = xreg)
ncxreg <- ncxreg + 1L
}
if (method == "CSS-ML") {
anyna <- anyNA(x)
if (ncxreg)
anyna <- anyna || anyNA(xreg)
if (anyna)
method <- "ML"
}
if (method == "CSS" || method == "CSS-ML") {
ncond <- order[2L] + seasonal$order[2L] * seasonal$period
ncond1 <- order[1L] + seasonal$period * seasonal$order[1L]
ncond <- ncond + if (!missing(n.cond))
max(n.cond, ncond1)
else ncond1
}
else ncond <- 0
if (is.null(fixed))
fixed <- rep(NA_real_, narma + ncxreg)
else if (length(fixed) != narma + ncxreg)
stop("wrong length for 'fixed'")
mask <- is.na(fixed)
no.optim <- !any(mask)
if (no.optim)
transform.pars <- FALSE
if (transform.pars) {
ind <- arma[1L] + arma[2L] + seq_len(arma[3L])
if (any(!mask[seq_len(arma[1L])]) || any(!mask[ind])) {
warning("some AR parameters were fixed: setting transform.pars = FALSE")
transform.pars <- FALSE
}
}
init0 <- rep.int(0, narma)
parscale <- rep(1, narma)
if (ncxreg) {
cn <- colnames(xreg)
orig.xreg <- (ncxreg == 1L) || any(!mask[narma + 1L:ncxreg])
if (!orig.xreg) {
S <- svd(na.omit(xreg))
xreg <- xreg %*% S$v
}
dx <- x
dxreg <- xreg
if (order[2L] > 0L) {
dx <- diff(dx, 1L, order[2L])
dxreg <- diff(dxreg, 1L, order[2L])
}
if (seasonal$period > 1L & seasonal$order[2L] > 0) {
dx <- diff(dx, seasonal$period, seasonal$order[2L])
dxreg <- diff(dxreg, seasonal$period, seasonal$order[2L])
}
fit <- if (length(dx) > ncol(dxreg))
lm(dx ~ dxreg - 1, na.action = na.omit)
else list(rank = 0L)
if (fit$rank == 0L) {
fit <- lm(x ~ xreg - 1, na.action = na.omit)
}
isna <- is.na(x) | apply(xreg, 1L, anyNA)
n.used <- sum(!isna) - length(Delta)
init0 <- c(init0, coef(fit))
ses <- summary(fit)$coefficients[, 2L]
parscale <- c(parscale, 10 * ses)
}
if (n.used <= 0)
stop("too few non-missing observations")
if (!is.null(init)) {
if (length(init) != length(init0))
stop("'init' is of the wrong length")
if (any(ind <- is.na(init)))
init[ind] <- init0[ind]
if (method == "ML") {
if (arma[1L] > 0)
if (!arCheck(init[1L:arma[1L]]))
stop("non-stationary AR part")
if (arma[3L] > 0)
if (!arCheck(init[sum(arma[1L:2L]) + 1L:arma[3L]]))
stop("non-stationary seasonal AR part")
if (transform.pars)
init <- .Call(C_ARIMA_Invtrans, as.double(init),
arma)
}
}
else init <- init0
coef <- as.double(fixed)
if (!("parscale" %in% names(optim.control)))
optim.control$parscale <- parscale[mask]
if (method == "CSS") {
res <- if (no.optim)
list(convergence = 0L, par = numeric(), value = armaCSS(numeric()))
else optim(init[mask], armaCSS, method = optim.method,
hessian = TRUE, control = optim.control)
if (res$convergence > 0)
warning(gettextf("possible convergence problem: optim gave code = %d",
res$convergence), domain = NA)
coef[mask] <- res$par
trarma <- .Call(C_ARIMA_transPars, coef, arma, FALSE)
mod <- makeARIMA(trarma[[1L]], trarma[[2L]], Delta, kappa,
SSinit)
if (ncxreg > 0)
x <- x - xreg %*% coef[narma + (1L:ncxreg)]
arimaSS(x, mod)
val <- .Call(C_ARIMA_CSS, x, arma, trarma[[1L]], trarma[[2L]],
as.integer(ncond), TRUE)
sigma2 <- val[[1L]]
var <- if (no.optim)
numeric()
else solve(res$hessian * n.used)
}
else {
if (method == "CSS-ML") {
res <- if (no.optim)
list(convergence = 0L, par = numeric(), value = armaCSS(numeric()))
else optim(init[mask], armaCSS, method = optim.method,
hessian = FALSE, control = optim.control)
if (res$convergence == 0)
init[mask] <- res$par
if (arma[1L] > 0)
if (!arCheck(init[1L:arma[1L]]))
stop("non-stationary AR part from CSS")
if (arma[3L] > 0)
if (!arCheck(init[sum(arma[1L:2L]) + 1L:arma[3L]]))
stop("non-stationary seasonal AR part from CSS")
ncond <- 0L
}
if (transform.pars) {
init <- .Call(C_ARIMA_Invtrans, init, arma)
if (arma[2L] > 0) {
ind <- arma[1L] + 1L:arma[2L]
init[ind] <- maInvert(init[ind])
}
if (arma[4L] > 0) {
ind <- sum(arma[1L:3L]) + 1L:arma[4L]
init[ind] <- maInvert(init[ind])
}
}
trarma <- .Call(C_ARIMA_transPars, init, arma, transform.pars)
mod <- makeARIMA(trarma[[1L]], trarma[[2L]], Delta, kappa,
SSinit)
res <- if (no.optim)
list(convergence = 0, par = numeric(), value = armafn(numeric(),
as.logical(transform.pars)))
else optim(init[mask], armafn, method = optim.method,
hessian = TRUE, control = optim.control, trans = as.logical(transform.pars))
if (res$convergence > 0)
warning(gettextf("possible convergence problem: optim gave code = %d",
res$convergence), domain = NA)
coef[mask] <- res$par
if (transform.pars) {
if (arma[2L] > 0L) {
ind <- arma[1L] + 1L:arma[2L]
if (all(mask[ind]))
coef[ind] <- maInvert(coef[ind])
}
if (arma[4L] > 0L) {
ind <- sum(arma[1L:3L]) + 1L:arma[4L]
if (all(mask[ind]))
coef[ind] <- maInvert(coef[ind])
}
if (any(coef[mask] != res$par)) {
oldcode <- res$convergence
res <- optim(coef[mask], armafn, method = optim.method,
hessian = TRUE, control = list(maxit = 0L,
parscale = optim.control$parscale), trans = TRUE)
res$convergence <- oldcode
coef[mask] <- res$par
}
A <- .Call(C_ARIMA_Gradtrans, as.double(coef), arma)
A <- A[mask, mask]
var <- crossprod(A, solve(res$hessian * n.used, A))
coef <- .Call(C_ARIMA_undoPars, coef, arma)
}
else var <- if (no.optim)
numeric()
else solve(res$hessian * n.used)
trarma <- .Call(C_ARIMA_transPars, coef, arma, FALSE)
mod <- makeARIMA(trarma[[1L]], trarma[[2L]], Delta, kappa,
SSinit)
val <- if (ncxreg > 0L)
arimaSS(x - xreg %*% coef[narma + (1L:ncxreg)], mod)
else arimaSS(x, mod)
sigma2 <- val[[1L]][1L]/n.used
}
value <- 2 * n.used * res$value + n.used + n.used * log(2 *
pi)
aic <- if (method != "CSS")
value + 2 * sum(mask) + 2
else NA
nm <- NULL
if (arma[1L] > 0L)
nm <- c(nm, paste0("ar", 1L:arma[1L]))
if (arma[2L] > 0L)
nm <- c(nm, paste0("ma", 1L:arma[2L]))
if (arma[3L] > 0L)
nm <- c(nm, paste0("sar", 1L:arma[3L]))
if (arma[4L] > 0L)
nm <- c(nm, paste0("sma", 1L:arma[4L]))
if (ncxreg > 0L) {
nm <- c(nm, cn)
if (!orig.xreg) {
ind <- narma + 1L:ncxreg
coef[ind] <- S$v %*% coef[ind]
A <- diag(narma + ncxreg)
A[ind, ind] <- S$v
A <- A[mask, mask]
var <- A %*% var %*% t(A)
}
}
names(coef) <- nm
if (!no.optim)
dimnames(var) <- list(nm[mask], nm[mask])
resid <- val[[2L]]
tsp(resid) <- xtsp
class(resid) <- "ts"
structure(list(coef = coef, sigma2 = sigma2, var.coef = var,
mask = mask, loglik = -0.5 * value, aic = aic, arma = arma,
residuals = resid, call = match.call(), series = series,
code = res$convergence, n.cond = ncond, nobs = n.used,
model = mod), class = "Arima")
}
Şimdi sıra ARIMA yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
ARIMA <- forecast(auto.arima(data), h=353)
Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “arima” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğuna aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(ARIMA)
today4<-today3[, -2:-3]
arima<-cbind(Tarih=today2, today4)
write.xlsx(arima, file = "arima.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
ARIMA yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra ARIMA yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
ARIMA <- forecast(auto.arima(data), h=353)
summary(ARIMA)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere ARIMA yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.5265276‘dır.
Forecast method: ARIMA(5,2,0)
Model Information:
Series: data
ARIMA(5,2,0)
Box Cox transformation: lambda= 0
Coefficients:
ar1 ar2 ar3 ar4 ar5
-0.7279 -0.6671 -0.5238 -0.3363 -0.1811
s.e. 0.0098 0.0117 0.0124 0.0117 0.0098
sigma^2 estimated as 0.0001656: log likelihood=29608.3
AIC=-59204.59 AICc=-59204.58 BIC=-59161.28
Error measures:
ME RMSE MAE MPE MAPE
Training set -0.0001702528 0.02194181 0.007389551 -0.01604272 0.5265276
MASE ACF1
Training set 0.02997334 0.05974482
Naive Yöntemi
Dolar alış kurunun tahmininde kullanılan dördüncü yöntem Naive olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, h = 10, level = c(80, 95), fan = FALSE, lambda = NULL,
biasadj = FALSE, ..., x = y)
{
fc <- rwf(x, h = h, level = level, fan = fan, lambda = lambda,
drift = FALSE, biasadj = biasadj, ...)
fc$model$call <- match.call()
fc$series <- deparse(substitute(y))
fc$method <- "Naive method"
return(fc)
}
Şimdi sıra Naive yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
naive <- naive(data, h=353)
autoplot(naive) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Naive Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “naive” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğunu aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(naive)
today4<-today3[, -2:-3]
naive<-cbind(Tarih=today2, today4)
write.xlsx(naive, file = "naive.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
Naive yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra Naive yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
naive <- naive(data, h=353)
summary(naive)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere Naive yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.4839495‘dir.
Forecast method: Naive method
Model Information:
Call: naive(y = data, h = 353)
Residual sd: 0.0204
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0005818318 0.02041678 0.006776669 0.1125204 0.4839495 0.02748738
ACF1
Training set 0.1624751
SES Yöntemi
Dolar alış kurunun tahmininde kullanılan beşinci yöntem SES olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, h = 10, level = c(80, 95), fan = FALSE, initial = c("optimal",
"simple"), alpha = NULL, lambda = NULL, biasadj = FALSE,
x = y, ...)
{
initial <- match.arg(initial)
if (initial == "optimal") {
fcast <- forecast(ets(x, "ANN", alpha = alpha,
opt.crit = "mse", lambda = lambda, biasadj = biasadj),
h, level = level, fan = fan, ...)
}
else {
fcast <- forecast(HoltWintersZZ(x, alpha = alpha, beta = FALSE,
gamma = FALSE, lambda = lambda, biasadj = biasadj),
h, level = level, fan = fan, ...)
}
fcast$method <- fcast$model$method <- "Simple exponential smoothing"
fcast$model$call <- match.call()
fcast$series <- deparse(substitute(y))
return(fcast)
}
Şimdi sıra SES yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
ses<-ses(data, h=353)
autoplot(ses) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("SES Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “ses” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğunu aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(ses)
today4<-today3[, -2:-3]
ses<-cbind(Tarih=today2, today4)
write.xlsx(ses, file = "ses.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
SES yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra SES yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
ses<-ses(data, h=353)
summary(ses)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere SES yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.5705732‘dir.
Forecast method: Simple exponential smoothing
Model Information:
Simple exponential smoothing
Call:
ses(y = data, h = 353)
Smoothing parameters:
alpha = 0.9999
Initial states:
l = -3e-04
sigma: 0.0204
AIC AICc BIC
14504.53 14504.53 14526.18
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0005818628 0.0204161 0.006776099 0.1991842 0.5705732 0.02748506
ACF1
Training set 0.1625604
Driftli Rassal Yürüyüş Yöntemi
Dolar alış kurunun tahmininde kullanılan yedinci yöntem Driftli Rassal Yürüyüş olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, h = 10, drift = TRUE, level = c(80, 95), fan = FALSE,
lambda = NULL, biasadj = FALSE, ..., x = y)
{
fit <- lagwalk(x, lag = 1, drift = drift, lambda = lambda,
biasadj = biasadj)
fc <- forecast(fit, h = h, level = level, fan = fan, lambda = fit$lambda,
biasadj = biasadj, ...)
fc$model$call <- match.call()
fc$series <- deparse(substitute(y))
if (drift) {
fc$method <- "Random walk with drift"
}
else {
fc$method <- "Random walk"
}
return(fc)
}
Şimdi sıra Drift yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
drift<-rwf(data, h = 353, drift = T)
autoplot(drift) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Drift Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “drift” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğunu aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(drift)
today4<-today3[, -2:-3]
drift<-cbind(Tarih=today2, today4)
write.xlsx(drift, file = "drift.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
Drift yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra Drift yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
drift<-rwf(data, h = 353, drift = T)
summary(drift)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere Drift yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 63.48552‘dir.
Forecast method: Random walk with drift
Model Information:
Call: rwf(y = data, h = 353, drift = T)
Drift: 6e-04 (se 2e-04)
Residual sd: 0.0204
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 2.8526e-17 0.02040849 0.007005999 -63.13675 63.48552 0.02841758
ACF1
Training set 0.1624751
Driftsiz Rassal Yürüyüş Yöntemi
Dolar alış kurunun tahmininde kullanılan yedinci yöntem Driftsiz Rassal Yürüyüş olup, bu yöntemin kullanımına aşağıda yer verilmiştir.
function (y, h = 10, drift = FALSE, level = c(80, 95), fan = FALSE,
lambda = NULL, biasadj = FALSE, ..., x = y)
{
fit <- lagwalk(x, lag = 1, drift = drift, lambda = lambda,
biasadj = biasadj)
fc <- forecast(fit, h = h, level = level, fan = fan, lambda = fit$lambda,
biasadj = biasadj, ...)
fc$model$call <- match.call()
fc$series <- deparse(substitute(y))
if (drift) {
fc$method <- "Random walk with drift"
}
else {
fc$method <- "Random walk"
}
return(fc)
}
Şimdi sıra Driftsiz yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
driftsiz<-rwf(data, h = 353, drift = F)
autoplot(driftsiz) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Driftsiz Rassal Yürüyüş Yöntemi İle Tahmin Edilen Dolar Alış
Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.

Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “driftsiz” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğuna aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(driftsiz)
today4<-today3[, -2:-3]
driftsiz<-cbind(Tarih=today2, today4)
write.xlsx(driftsiz, file = "driftsiz.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz
Driftsiz yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra Driftsiz yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
driftsiz<-rwf(data, h = 353, drift = F)
summary(driftsiz)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere Driftsiz yöntem, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.4839495‘tir.
Forecast method: Random walk
Model Information:
Call: rwf(y = data, h = 353, drift = F)
Residual sd: 0.0204
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0005818318 0.02041678 0.006776669 0.1125204 0.4839495 0.02748738
ACF1
Training set 0.1624751
Holt Metodu
Dolar alış kurunun tahmininde kullanılan sekizinci yöntem Holt olup, bu yöntemin kullanımına aşağıda yer verilmiştir.
holt(
y,
h = 10,
damped = FALSE,
level = c(80, 95),
fan = FALSE,
initial = c("optimal", "simple"),
exponential = FALSE,
alpha = NULL,
beta = NULL,
phi = NULL,
lambda = NULL,
biasadj = FALSE,
x = y,
...
)
Şimdi sıra Holt yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur. Kurulan bu modelden sonuçların elde edilmesi diğer yöntemlere göre daha uzun sürmektedir.
holt <- holt(data, h=353)
autoplot(holt) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Holt Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.
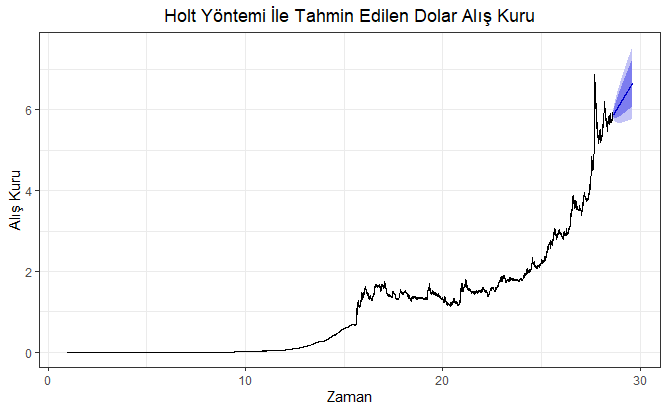
Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “holt” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğuna aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(holt)
today4<-today3[,-2:-3]
holt<-cbind(Tarih=today2, today4)
write.xlsx(holt, file = "holt.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
Holt yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra Holt yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
holt <- holt(data, h=353)
summary(holt)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere ELM yöntemi, dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 108.3473‘tür.
Forecast method: Holt's method
Model Information:
Holt's method
Call:
holt(y = data, h = 353)
Smoothing parameters:
alpha = 0.9999
beta = 0.001
Initial states:
l = -0.2047
b = 6e-04
sigma: 0.0205
AIC AICc BIC
14596.25 14596.26 14632.35
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0001682216 0.02050503 0.006873361 7.650097 108.3473 0.02787958
ACF1
Training set 0.1597678
NNAR Metodu
Dolar alış kurunun tahmininde kullanılan sekizinci yöntem ileri beslemeli ve tek gizli tabakalı (feed-forward neural networks with a single hidden layer) olan NNAR (Neural Network Auto Regression) olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, p, P = 1, size, repeats = 20, xreg = NULL, lambda = NULL,
model = NULL, subset = NULL, scale.inputs = TRUE, x = y,
...)
{
useoldmodel <- FALSE
yname <- deparse(substitute(y))
if (!is.null(model)) {
useoldmodel <- TRUE
if (!is.nnetar(model)) {
stop("Model must be a nnetar object")
}
m <- max(round(frequency(model$x)), 1L)
minlength <- max(c(model$p, model$P * m)) + 1
if (length(x) < minlength) {
stop(paste("Series must be at least of length",
minlength, "to use fitted model"))
}
if (tsp(as.ts(x))[3] != m) {
warning(paste("Data frequency doesn't match fitted model, coercing to frequency =",
m))
x <- ts(x, frequency = m)
}
if (!is.null(model$xreg)) {
if (is.null(xreg)) {
stop("No external regressors provided")
}
if (NCOL(xreg) != NCOL(model$xreg)) {
stop("Number of external regressors does not match fitted model")
}
}
lambda <- model$lambda
size <- model$size
p <- model$p
P <- model$P
if (P > 0) {
lags <- sort(unique(c(1:p, m * (1:P))))
}
else {
lags <- 1:p
}
if (is.null(model$scalex)) {
scale.inputs <- FALSE
}
}
else {
if (length(y) < 3) {
stop("Not enough data to fit a model")
}
constant_data <- is.constant(na.interp(x))
if (constant_data) {
warning("Constant data, setting p=1, P=0, lambda=NULL, scale.inputs=FALSE")
scale.inputs <- FALSE
lambda <- NULL
p <- 1
P <- 0
}
if (!is.null(xreg)) {
constant_xreg <- any(apply(as.matrix(xreg), 2, function(x) is.constant(na.interp(x))))
if (constant_xreg) {
warning("Constant xreg column, setting scale.inputs=FALSE")
scale.inputs <- FALSE
}
}
}
if (any(is.na(x))) {
warning("Missing values in x, omitting rows")
}
if (!is.null(lambda)) {
xx <- BoxCox(x, lambda)
lambda <- attr(xx, "lambda")
}
else {
xx <- x
}
xsub <- rep(TRUE, length(x))
if (is.numeric(subset)) {
xsub[-subset] <- FALSE
}
if (is.logical(subset)) {
xsub <- subset
}
scalex <- NULL
if (scale.inputs) {
if (useoldmodel) {
scalex <- model$scalex
}
else {
tmpx <- scale(xx[xsub], center = TRUE, scale = TRUE)
scalex <- list(center = attr(tmpx, "scaled:center"),
scale = attr(tmpx, "scaled:scale"))
}
xx <- scale(xx, center = scalex$center, scale = scalex$scale)
xx <- xx[, 1]
}
xxreg <- NULL
scalexreg <- NULL
if (!is.null(xreg)) {
xxreg <- xreg <- as.matrix(xreg)
if (length(x) != NROW(xreg)) {
stop("Number of rows in xreg does not match series length")
}
if (any(is.na(xreg))) {
warning("Missing values in xreg, omitting rows")
}
if (scale.inputs) {
if (useoldmodel) {
scalexreg <- model$scalexreg
}
else {
tmpx <- scale(xxreg[xsub, ], center = TRUE, scale = TRUE)
scalexreg <- list(center = attr(tmpx, "scaled:center"),
scale = attr(tmpx, "scaled:scale"))
}
xxreg <- scale(xxreg, center = scalexreg$center,
scale = scalexreg$scale)
}
}
n <- length(xx)
xx <- as.ts(xx)
m <- max(round(frequency(xx)), 1L)
if (!useoldmodel) {
if (m == 1) {
if (missing(p)) {
p <- max(length(ar(na.interp(xx))$ar), 1)
}
if (p >= n) {
warning("Reducing number of lagged inputs due to short series")
p <- n - 1
}
lags <- 1:p
if (P > 1) {
warning("Non-seasonal data, ignoring seasonal lags")
}
P <- 0
}
else {
if (missing(p)) {
if (n > 2 * m) {
x.sa <- seasadj(mstl(na.interp(xx)))
}
else {
x.sa <- na.interp(xx)
}
p <- max(length(ar(x.sa)$ar), 1)
}
if (p >= n) {
warning("Reducing number of lagged inputs due to short series")
p <- n - 1
}
if (P > 0 && n >= m * P + 2) {
lags <- sort(unique(c(1:p, m * (1:P))))
}
else {
lags <- 1:p
if (P > 0) {
warning("Series too short for seasonal lags")
P <- 0
}
}
}
}
maxlag <- max(lags)
nlag <- length(lags)
y <- xx[-(1:maxlag)]
lags.X <- matrix(NA_real_, ncol = nlag, nrow = n - maxlag)
for (i in 1:nlag) lags.X[, i] <- xx[(maxlag - lags[i] + 1):(n -
lags[i])]
lags.X <- cbind(lags.X, xxreg[-(1:maxlag), ])
if (missing(size)) {
size <- round((NCOL(lags.X) + 1)/2)
}
j <- complete.cases(lags.X, y)
j <- j & xsub[-(1:maxlag)]
if (NROW(lags.X[j, , drop = FALSE]) == 0) {
stop("No data to fit (possibly due to NA or NaN)")
}
if (useoldmodel) {
fit <- oldmodel_avnnet(lags.X[j, , drop = FALSE], y[j],
size = size, model)
}
else {
fit <- avnnet(lags.X[j, , drop = FALSE], y[j], size = size,
repeats = repeats, ...)
}
out <- list()
out$x <- as.ts(x)
out$m <- m
out$p <- p
out$P <- P
out$scalex <- scalex
out$scalexreg <- scalexreg
out$size <- size
out$xreg <- xreg
out$lambda <- lambda
out$subset <- (1:length(x))[xsub]
out$model <- fit
out$nnetargs <- list(...)
if (useoldmodel) {
out$nnetargs <- model$nnetargs
}
if (NROW(lags.X[j, , drop = FALSE]) == 1) {
fits <- c(rep(NA_real_, maxlag), mean(sapply(fit, predict)))
}
else {
fits <- c(rep(NA_real_, maxlag), rowMeans(sapply(fit,
predict)))
}
if (scale.inputs) {
fits <- fits * scalex$scale + scalex$center
}
fits <- ts(fits)
if (!is.null(lambda)) {
fits <- InvBoxCox(fits, lambda)
}
out$fitted <- ts(rep(NA_real_, length(out$x)))
out$fitted[c(rep(TRUE, maxlag), j)] <- fits
tsp(out$fitted) <- tsp(out$x)
out$residuals <- out$x - out$fitted
out$lags <- lags
out$series <- yname
out$method <- paste("NNAR(", p, sep = "")
if (P > 0) {
out$method <- paste(out$method, ",", P, sep = "")
}
out$method <- paste(out$method, ",", size, ")",
sep = "")
if (P > 0) {
out$method <- paste(out$method, "[", m, "]",
sep = "")
}
out$call <- match.call()
return(structure(out, class = c("nnetar")))
}
Şimdi sıra NNAR yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur. Kurulan bu modelden sonuçların elde edilmesi diğer yöntemlere göre daha uzun sürmektedir.
model <- nnetar(data, lambda=0)
nnar <- forecast(model,h=353)
autoplot (nnar) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Driftsiz Rassal Yürüyüş Yöntemi İle Tahmin Edilen Dolar
Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.
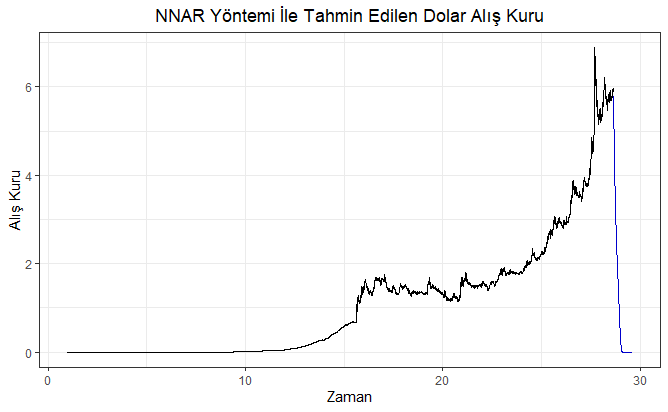
Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “nnar” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğuna aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(nnar)
today4<-today3
nnar<-cbind(Tarih=today2, today4)
write.xlsx(nnar, file = "nnar.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
NNAR yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra NNAR yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
model <- nnetar(data, lambda=0)
nnar <- forecast(model,h=353)
summary(nnar)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere NNAR yönteminin dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.6250022’dir.
Forecast method: NNAR(1,1,2)[365]
Model Information:
Average of 20 networks, each of which is
a 2-2-1 network with 9 weights
options were - linear output units
Error measures:
ME RMSE MAE MPE MAPE
Training set 0.001965417 0.02524943 0.008746252 -0.004684467 0.6250022
MASE ACF1
Training set 0.03547636 0.4467661
Theta Metodu
Dolar alış kurunun tahmininde kullanılan onuncu yöntem Theta olup, bu yöntemin algoritmasına aşağıda yer verilmiştir.
function (y, h = ifelse(frequency(y) > 1, 2 * frequency(y), 10),
level = c(80, 95), fan = FALSE, x = y)
{
if (fan) {
level <- seq(51, 99, by = 3)
}
else {
if (min(level) > 0 && max(level) < 1) {
level <- 100 * level
}
else if (min(level) < 0 || max(level) > 99.99) {
stop("Confidence limit out of range")
}
}
n <- length(x)
x <- as.ts(x)
m <- frequency(x)
if (m > 1 && !is.constant(x) && n > 2 * m) {
r <- as.numeric(acf(x, lag.max = m, plot = FALSE)$acf)[-1]
stat <- sqrt((1 + 2 * sum(r[-m]^2))/n)
seasonal <- (abs(r[m])/stat > qnorm(0.95))
}
else {
seasonal <- FALSE
}
origx <- x
if (seasonal) {
decomp <- decompose(x, type = "multiplicative")
if (any(abs(seasonal(decomp)) < 1e-10))
warning("Seasonal indexes equal to zero. Using non-seasonal Theta method")
else x <- seasadj(decomp)
}
fcast <- ses(x, h = h)
tmp2 <- lsfit(0:(n - 1), x)$coef[2]/2
alpha <- pmax(1e-10, fcast$model$par["alpha"])
fcast$mean <- fcast$mean + tmp2 * (0:(h - 1) + (1 - (1 -
alpha)^n)/alpha)
if (seasonal) {
fcast$mean <- fcast$mean * rep(tail(decomp$seasonal,
m), trunc(1 + h/m))[1:h]
fcast$fitted <- fcast$fitted * decomp$seasonal
}
fcast$residuals <- origx - fcast$fitted
fcast.se <- sqrt(fcast$model$sigma) * sqrt((0:(h - 1)) *
alpha^2 + 1)
nconf <- length(level)
fcast$lower <- fcast$upper <- ts(matrix(NA, nrow = h, ncol = nconf))
tsp(fcast$lower) <- tsp(fcast$upper) <- tsp(fcast$mean)
for (i in 1:nconf) {
zt <- -qnorm(0.5 - level[i]/200)
fcast$lower[, i] <- fcast$mean - zt * fcast.se
fcast$upper[, i] <- fcast$mean + zt * fcast.se
}
fcast$x <- origx
fcast$level <- level
fcast$method <- "Theta"
fcast$model <- list(alpha = alpha, drift = tmp2, sigma = fcast$model$sigma)
fcast$model$call <- match.call()
return(fcast)
}
Şimdi sıra Theta yöntemi kullanılarak modelin oluşturulmasına gelmiştir. Dolar alış kuruna ait 353 günlük bir zaman serisi için tahmin yapılacağı için aşağıdaki R kod bloğunda h=353 olarak belirlenmiştir. Kurulan modele, kurulan modelden üretilen tahminlere ilişkin grafik için R kod bloğu bir bütün olarak aşağıda sunulmuştur.
theta<-thetaf(data, h=353)
autoplot(theta) +
ylab("Alış Kuru") +
xlab("Zaman") +
ggtitle("Theta Yöntemi İle Tahmin Edilen Dolar Alış Kuru") +
theme_bw()+
theme(plot.title = element_text(hjust = 0.5))
Yukarıdaki kod bloğunun çalıştırılmasından sonra elde edilen güven aralıklı (CI: Confidence Interval) 353 günlük dolar kuru tahminleri aşağıdaki şekilde verilmiştir. Burada, maviyle gösterilen alan güven aralıklarıyla birlikte dolar alış kuru tahminlerini, önceki alan ise mevcut dolar alış kuru gerçekleşmelerini göstermektedir. Maviyle gösterilen alanda yer alan eğri ise nokta tahmin (point forecast)’leri göstermektedir.
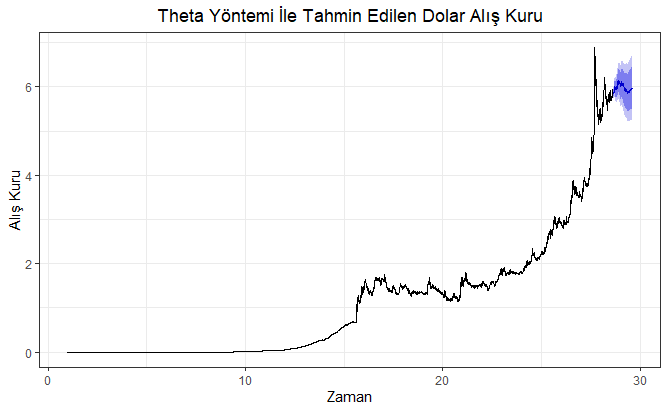
Elde edilen 353 günlük dolar alış kuru tahmin değerleri, tahmin edilen tarih ile bu tarihlere ait dolar alış kur değerleri xlsx (Microsoft Office Excel) uzantılı “theta” adlı dosyaya yazdırılmıştır. Bahsedilen bu işlemleri gösterir R kod bloğuna aşağıda yer verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(theta)
today4<-today3[,-2:-3]
theta<-cbind(Tarih=today2, today4)
write.xlsx(theta, file = "theta.xlsx",
sheetName = "tahmin_aliskuru", append = FALSE)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra elde edilen tahmini dolar alış kur değerleri tahmin edilen tarihe göre güven aralıkları ile birlikte xlsx uzantılı olarak aşağıda verilmiştir. Buradaki linkten sonuçları indirebilirsiniz.
Theta yönteminin ortaya koyduğu hata türlerinden MAPE (Mean Absolute Percentage Error) değerine bakalım. Bu amaçla aşağıdaki R kod bloğu çalıştırıldıktan sonra Theta yönteminin sonuçlarına bakılarak MAPE ve diğer hata türlerine ulaşılabilir.
theta<-thetaf(data, h=353)
summary(theta)
Yukarıdaki kod bloğunun çalıştılmasından sonra aşağıdaki sonuçlardan da görüleceği üzere Theta yönteminin dolar alış kuru tahminlerinde ürettiği MAPE hata değeri 0.5917247‘dir.
Forecast method: Theta
Model Information:
$alpha
[1] 0.9999
$drift
X
0.0002007181
$sigma
[1] 0.0003995984
$call
thetaf(y = data, h = 353)
Error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0005853508 0.01998895 0.006803491 0.2005714 0.5917247 0.02759617
ACF1
Training set 0.1619785
SONUÇ
Hacim olarak oldukça güvenilir 40 yıllık günlük Dolar-TL alış kuru veri setinin kullanılması başlı başına çok değerli çıkarımlar ortaya konulmasına katkı sağladığından oluşturulan model farklı yöntemlerle karşılaştırmalı olarak test edilerek MAPE (Mean Absolute Percentage Error) değerleri açsısından en iyi yöntemin hangisinin olduğuna karar verilmiştir. Deneysel olarak Merkez Bankası veri tabanından 02.01.1980 tarihinden 13.01.2020 tarihine kadar (dahil) indirilmiş dolar alış kuru verisi üzerinden 31.12.2020 tarihine kadar (dahil) geçen 353 günlük bir tahmin yapılmıştır. Tahminler yapılırken otomatik (default) olarak veri seti kullanılan yöntem içerisinde eğitilerek (training) aşağıda yer alan yöntemlerle Dolar-TL alış kuru tahmin edilmiştir.
- TBATS (Exponential smoothing state space model with Box-Cox transformation, ARMA errors, Trend and Seasonal components)
- ARIMA (Autoregressive Integrated Moving Average)
- ETS (Exponential Smoothing State Space Model)
- Naive
- NNAR (Neural Network Autoregression): Otoregresyon Sinir Ağı
- Holt
- SES (Simple Exponential Smoothing)
- Driftli Rassal Yürüyüş Yöntemi (Random Walk Forecast with Drift)
- Driftsiz Rassal Yürüyüş Yöntemi (Random Walk Forecast without Drift)
- Theta
Yukarıdaki bahsedilen yöntemlerle dolar alış kur değerleri tahmin edildikten sonra elde edilen Dolar-TL alış kur değerlerine göre tahmin yöntemleri hata oranları açısından karşılaştırılmıştır. Bu bağlamda kullanılan hata oranları göstergesi olarak MAPE (Mean Absolute Percentage Error)‘den yararlanılmıştır. MAPE hata değeri en düşük olan tahmin yöntemi Dolar-TL alış kuru tahminleri açısından en iyi yöntem olarak belirlenmiştir. Ancak istenirse önceki kısımlarda diğer hata türlerine de yer verildiğinden bu hata türleri açısından kullanılan tahmin yöntemleri karşılaştırılabilir.
Döviz alış kuru tahminlerine bakıldığında MAPE hata değerleri, kullanılan 10 tahmin yöntemine göre aşağıdaki kod bloğunda verilmiştir.
Yontem<-c("TBATS","ETS", "ARIMA", "Naive", "SES","Driftli Rassal Yürüyüş",
"Driftsiz Rassal Yürüyüş","Holt","NNAR", "Theta")
MAPE_Hata_Değerleri<-c(0.4897634, 0.505253, 0.5265276, 0.4839495,
0.5705732,63.48552, 0.4839495, 108.3473, 0.6250022,
0.5917247)
tablo<-tibble(Yöntem=Yontem, MAPE=MAPE_Hata_Değerleri)
t1<-tablo %>% arrange((MAPE))
formattable(t1)
Yukarıdaki R kod bloğu çalıştırıldıktan sonra kullanılan tahmin yöntemine göre ortaya konulan MAPE hata değerleri aşağıdaki tabloda verilmiştir. Literatürde MAPE değerleri en düşük olan tahmin metodu diğer metotlara göre daha iyi olduğu kabul edilmektedir.
Kullanılan Tahmin Yöntemine Göre MAPE Hata Değerleri

Yukarıdaki tabloda MAPE değerlerine bakıldığında en iyi ilk üç tahmin yönteminin sırasıyla Naive, Driftsiz Rassal Yürüyüş ve TBATS yöntemleri olduğu görülmektedir. Bu üç yöntemin 31.12.2020 dönem sonuna kadar (bu tarih dahil) tahminlerine yukarıdaki bölümlerde yer verilmiştir. Sonuçlar bu bölümlerdeki linklerden xlsx uzantılı olarak indirilebilir. Ancak kullanılan tahmin sonuçlarına gerek ulaşım kolaylığı gerekse bir bütün olarak bir arada görülebilmesi adına yöntemlerden üretilen MAPE değerlerine göre aşağıda verilmiştir. Buradaki linklerden kullanılan tahmin yöntemine göre Dolar-TL alış kuru tahmin sonuçları indirilebilir.
Naive Yöntemi
Driftsiz Rassal Yürüyüş Yöntemi
TBATS Yöntemi
ETS Yöntemi
ARIMA Yöntemi
SES Yöntemi
Theta Yöntemi
NNAR Yöntemi
Driftli Rassal Yürüyüş Yöntemi
Holt Yöntemi
MAPE hata değerleri en düşük İlk 4 yönteme göre ortaya konulan 2020 yılı sonu son 10 Dolar-TL alış kur tahmin sonuçları TBATs yönteminden başlanarak verilmiştir.
TBATS Yöntemi Dolar-TL Alış Kuru Tahmin Sonuçları
TBATS yöntemi 2020 yılı sonu son 10 tahmin sonuçlarına ilişkin R kod bloğu aşağıda verilmiştir.
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(sonuc)
today4<-today3[, -2:-5]
tbats<-tibble(Tarih=today2,Nokta_Tahmin=digits(today4$`Point Forecast`, 4))
tbats10<-tail(tbats,10)
formattable(tbats10,
align = c("l","c"),
list('Tarih' = formatter("span", style = ~ style(color = "grey", font.weight = "bold")),
'Nokta_Tahmin' = color_bar("#FA614B"), digits('Nokta_Tahmin',4)))
Yukarıdaki R kod bloğu çalıştırıldıktan sonra TBATS yöntemine göre ortaya konulan 2020 yılı sonu son 10 Dolar-TL alış kuru tahmini tarihe göre aşağıdaki tabloda verilmiştir.

TBATS yöntemi kullanılarak ortaya konulan 353 günlük Dolar-TL alış kuru seyri ise aşağıdaki R kod bloğunda verilmiştir.
tbats<-zoo(tbats[,2], seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1))
tbats<-as.xts(tbats)
plot(tbats, main="TBATS: 2020 Yılı Dolar-TL Alış Kuru Tahminleri", col="red", cex.main=0.6, cex.lab=1)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra TBATS yönteminden elde edilen Dolar-TL alış kuru tahmin değerlerinin seyri aşağıdaki grafikte verilmiştir.
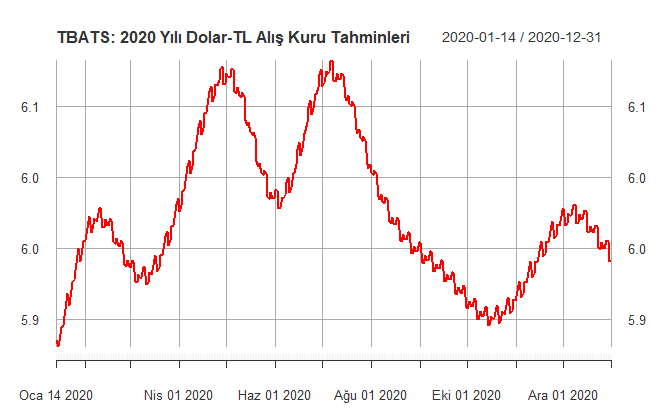
Naive ve Driftsiz Rassal Yürüyüş Yöntemlerine Göre Dolar-TL Alış Kuru Tahmin Sonuçları
Bu iki yönteme göre 14.01.2020 tarihinden 31.12.2020 tarihine kadar (dahil) tahmin edilen Dolar-TL alış kuru tahmin değeri 5.817’dir. Her iki yöntemden elde edilen nokta kur tahmin değerleri aynı olup, güven aralıkları sadece farklılık göstermektedir.
ETS Yöntemi Dolar-TL Alış Kuru Tahmin Sonuçları
ETS yöntemi 2020 yılı sonu son 10 tahmin sonuçlarına ilişkin R kod bloğu aşağıda verilmiştir.
ETS <- forecast(tev, h=353)
today1 <- seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1)
today2<-format(today1, format="%d/%m/%Y")
today3<-as_tibble(ETS)
today4<-today3[, -2:-5]
ets<-tibble(Tarih=today2,Nokta_Tahmin=digits(today4$`Point Forecast`, 7))
ets10<-tail(ets,10)
formattable(ets10,
align = c("l","c"),
list('Tarih' = formatter("span", style = ~ style(color = "grey", font.weight = "bold")),
'Nokta_Tahmin' = color_bar("#FA614B")))
Yukarıdaki R kod bloğu çalıştırıldıktan sonra ETS yöntemine göre ortaya konulan 2020 yılı sonu son 10 Dolar-TL alış kuru tahmini tarihe göre aşağıdaki tabloda verilmiştir.
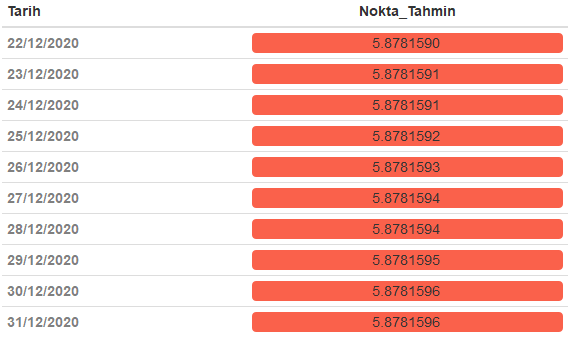
ETS yöntemi kullanılarak ortaya konulan 353 günlük Dolar-TL alış kuru seyri ise aşağıdaki R kod bloğunda verilmiştir.
ets<-zoo(ets[,2], seq(from = as.Date("2020-01-14"), to = as.Date("2020-12-31"), by = 1))
ets<-as.xts(ets)
plot(ets, main="ETS: 2020 Yılı Dolar-TL Alış Kuru Tahminleri", col="red", cex.main=0.6, cex.lab=1)
Yukarıdaki R kod bloğunun çalıştırılmasından sonra ETS yönteminden elde edilen Dolar-TL alış kuru tahmin değerlerinin seyri aşağıdaki grafikte verilmiştir.
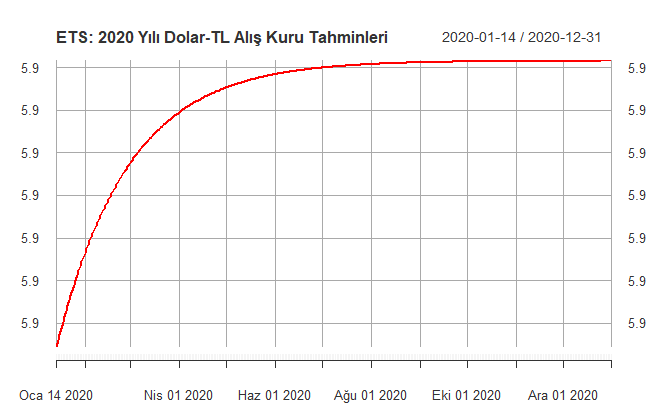
Bu çalışma özellikle dolar kuru tahminlerinde bilimselliğe dayalı olarak çok farklı ve sayıda tahmin metotlarının bir arada karşılaştırmalı olarak kullanıldığı ilk çalışma olması açısından son derece büyük önem arz etmektedir.
Faydalı olması ve farkındalık oluşturması dileğiyle.
Bilimle ve teknolojiyle kalınız.
Saygılarımla…
Not: Kaynak gösterilmeden alıntı yapılamaz veya kopyalanamaz.
Note: It can not be cited or copied without referencing.
Yararlanılan Kaynaklar (References)
Assimakopoulos, V. and Nikolopoulos, K. (2000). The theta model: a decomposition approach to forecasting. International Journal of Forecasting 16, 521-530.
Hyndman, R.J., and Billah, B. (2003) Unmasking the Theta method. International J. Forecasting, 19, 287-290.
https://www.r-project.org/
De Livera, Alysha M. “Automatic forecasting with a modified exponential smoothing state space framework.” Monash Econometrics and Business Statistics Working Papers 10, no. 10 (2010).
De Livera, Alysha M., Rob J. Hyndman, and Ralph D. Snyder. “Forecasting time series with complex seasonal patterns using exponential smoothing.” Journal of the American Statistical Association 106, no. 496 (2011): 1513-1527.
http://tagteam.harvard.edu/hub_feeds/1981/feed_items/273923
http://trap.ncirl.ie/3424/1/sonaligupta.pdf
https://pdfs.semanticscholar.org/65d4/7c33e1a4f01c45c44479df3356ad191dafb6.pdf
Antonio Preti & Gianluca Lentini (2016) Forecast models for suicide: Time-series analysis with data from Italy, Chronobiology International, 33:9, 1235-1246, DOI:10.1080/07420528.2016.1211669
https://yintingchou.com/posts/bats-and-tbats-model/
https://michaeltoth.me/the-ultimate-opinionated-guide-to-base-r-date-format-functions.html
https://robjhyndman.com/publications/complex-seasonality/
https://otexts.com/fpp2/combinations.html
https://tevfikbulut.com/2019/09/30/doviz-kurlarindaki-dalga-boylarinin-hesaplanmasina-yonelik-yontem-onerileri-ii-wt-ve-ct-yontemleri/
Hyndman, R.J., Koehler, A.B., Snyder, R.D., and Grose, S. (2002) “A state space framework for automatic forecasting using exponential smoothing methods”, International J. Forecasting, 18(3), 439–454.
Hyndman, R.J., Akram, Md., and Archibald, B. (2008) “The admissible parameter space for exponential smoothing models”. Annals of Statistical Mathematics, 60(2), 407–426.
Hyndman, R.J., Koehler, A.B., Ord, J.K., and Snyder, R.D. (2008) Forecasting with exponential smoothing: the state space approach, Springer-Verlag. http://www.exponentialsmoothing.net.
Hyndman and Athanasopoulos (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. https://OTexts.org/fpp2/
For an introduction to neural networks see: Ord K., Fildes R., Kourentzes N. (2017) Principles of Business Forecasting 2e. Wessex Press Publishing Co., Chapter 10.
For combination operators see: Kourentzes N., Barrow B.K., Crone S.F. (2014) Neural network ensemble operators for time series forecasting. Expert Systems with Applications, 41(9), 4235-4244.
For variable selection see: Crone S.F., Kourentzes N. (2010) Feature selection for time series prediction A combined filter and wrapper approach for neural networks. Neurocomputing, 73(10), 1923-1936.
For ELMs see: Huang G.B., Zhou H., Ding X. (2006) Extreme learning machine: theory and applications. Neurocomputing, 70(1), 489-501.
https://pdfs.semanticscholar.org/93b7/9de5d49e26e933b5a731318390fe907d4957.pdf
https://cran.r-project.org/web/packages/nnfor/nnfor.pdf
https://cran.r-project.org/web/packages/forecast/vignettes/JSS2008.pdf
https://otexts.com/fpp2/nnetar.html
https://arxiv.org/ftp/arxiv/papers/1401/1401.1333.pdf
Assimakopoulos, V. and Nikolopoulos, K. (2000). The theta model: a decomposition approach to forecasting. International Journal of Forecasting 16, 521-530.
https://tevfikbulut.com/2020/01/06/dolar-kurunun-tahmini-uzerine-bir-vaka-calismasi-a-case-study-on-forecast-of-usd-exchange-rate/
https://tevfikbulut.com/2019/09/30/doviz-kurlarindaki-dalga-boylarinin-hesaplanmasina-yonelik-yontem-onerileri-ii-wt-ve-ct-yontemleri/
T.C. Merkez Bankası:https://evds2.tcmb.gov.tr/index.php?/evds/serieMarket/#collapse_2. Ulaşım Tarihi: 13/01/2020.
Türkiye Cumhuriyeti Devletinin Para Birimi Hakkında Kanun,
Kanun No: 5083, Resmi Gazete Tarihi: 31/01/2004, Resmi Gazete Sayısı: 25363 http://www.resmigazete.gov.tr/eskiler/2004/01/20040131.htm#3.Ulaşım Tarihi: 19/02/2019.
Tukey, J. W. (1993). Exploratory Data Analysis: Past, Present, and Future. Princeton University, Department of Statistics, Technical Report No:302. https://apps.dtic.mil/dtic/tr/fulltext/u2/a266775.pdf. Ulaşım Tarihi: 19/02/2019.
Döviz Kurlarındaki Dalga Boylarının Hesaplanmasına Yönelik Yöntem Önerileri: Wt ve Ct Yöntemleri: https://tevfikbulut.com/2019/02/24/21-yillik-doviz-verisinin-kesifsel-analizi/
https://www.r-project.org/
Hyndman, R.J., and Billah, B. (2003) Unmasking the Theta method. International J. Forecasting, 19, 287-290.